Геометрия – чрезвычайно интересная наука, которую начинают преподавать в российских школах в седьмом классе. Но иногда тема, пройденная на уроке, совсем не понятна, а попытки прочитать параграф в учебнике только усугубляют ситуацию. Тогда на помощь приходит всезнающий Интернет или же некоторые ученики просто открывают готовые домашние задания, что в корне неверно, ведь тогда вопрос остается без ответа, мозг не развивается, возникают еще большие проблемы с восприятием информации на уроке, что ведет к плохим оценкам. В этой статье мы разберем один из базовых элементов, при помощи которого решаются очень многие задачи. Каково определение высоты треугольника? Как ее строить? Ответы на эти и многие другие вопросы вы найдете в этой статье.
Определение высоты треугольника
Понимание сути элемента, и зачем он нужен, начинается всегда с изучения теории. Так, высота треугольника – перпендикуляр, опущенный из вершины треугольника на прямую, содержащую противоположную сторону. Почему не на саму сторону? С этим мы разберемся немного позже.
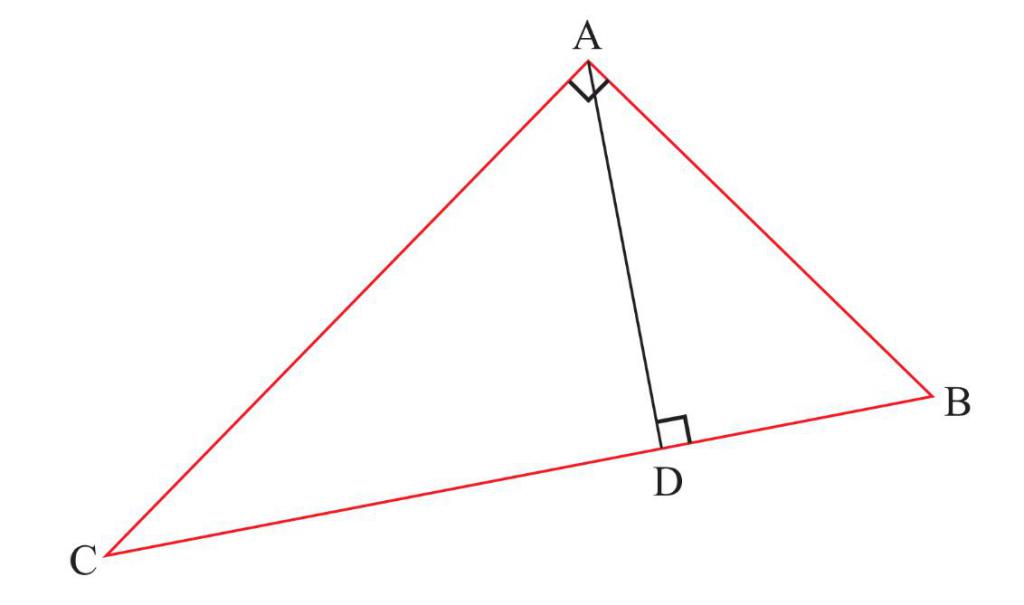
Сколько можно провести высот в треугольнике? Количество высот совпадает с количеством вершин, то есть три. Все три пересечения перпендикуляров треугольника пересекаются в одной точке.
Давайте также повторим теорию о двух других важных элементах – биссектрисе и медиане.
Биссектриса – луч, соединяющий вершину треугольника с противоположной стороной, при этом разделяя угол на две равные части.
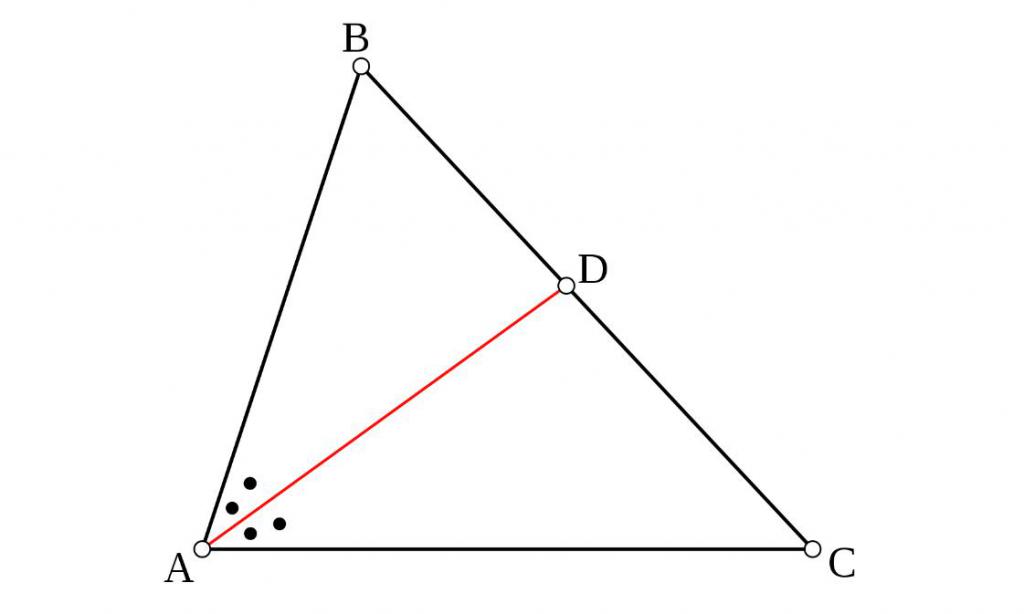
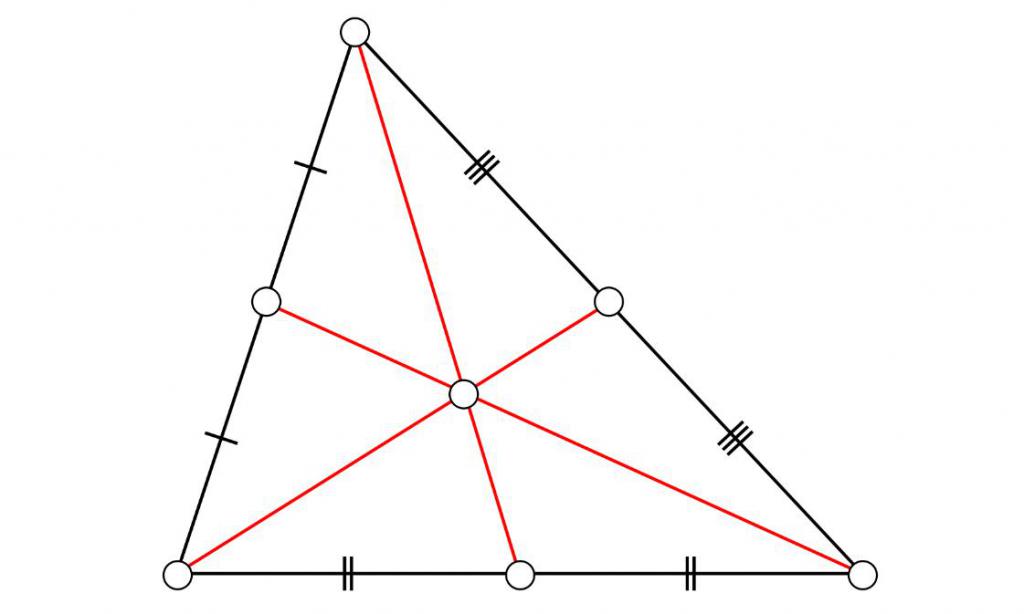
Медиана – отрезок, соединяющий вершину угла с серединой противоположной стороны.
Типы треугольников
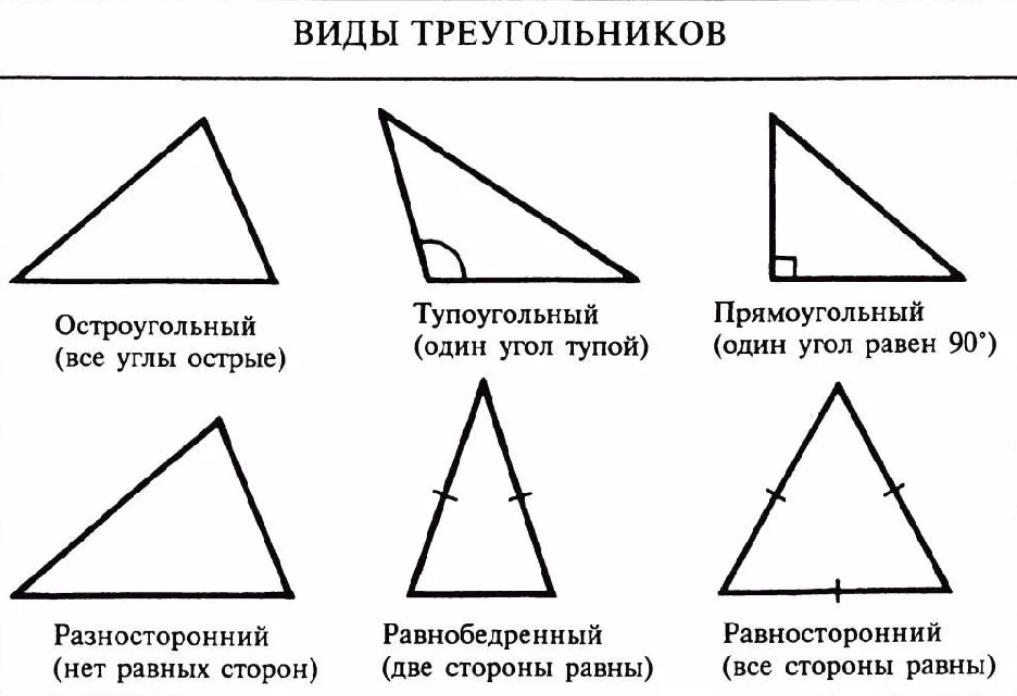
Разновидностей треугольников в геометрии очень много, в каждом из них высоты играют свою роль. Давайте рассмотрим подробно все типы этой фигуры. Определение высоты треугольника поможет нам в этом.
Начнем с обычного остроугольного разностороннего треугольника, у которого все углы острые и не равны 60 градусам, а стороны не равны друг другу. В этой геометрической фигуре высоты пересекутся, но эта точка не будет центром треугольника.
В тупоугольном треугольнике градусная мера одного угла больше 90 градусов. Высоту, выходящую из тупого угла, опускают на прямую, содержащую противоположную сторону.
Следующим будет равнобедренный треугольник. У него равны только две стороны и два угла при основании. Интересно то, что высота, проведенная из вершины к основанию треугольника, совпадает с медианой и биссектрисой.
В равностороннем треугольнике равны все стороны и углы, которые равны 60 градусов (каждый). Все высоты, медианы и биссектрисы совпадают и пересекаются в одной точке – центре треугольника.
Стандартные формулы, связанные с высотой
Для каждого из вышеперечисленных случаев есть формулы для определения высоты, но в этом пункте мы рассмотрим лишь те, что подходят для каждого типа треугольника. Таких формул четыре.
- Самая простая и доступная: H = 2S/a. Зная площадь и длину стороны, к которой опущен перпендикуляр, мы можем найти высоту, разделив двойное произведение площади на сторону.
- Если треугольник заключен в окружность, то и на этот случай есть формула: H = bc/2R. Для нахождения высоты, нужно стороны, на которые не падает перпендикуляр, разделить на двойное произведение радиуса описанной вокруг треугольника окружности.
- Зная только стороны, мы также можем найти высоту: H = (2√(p(p-a)*(p-b)*(p-c)))/a, где: p – полупериметр; a – сторона, на которую опущена высота; b, c – стороны, на которые не падает перпендикуляр.
- А для тех, кто знает уже начал проходить тригонометрию и знает, что такое синус и косинус, существует такая формула: H = bsinY = csinB. Синус – отношение противолежащей стороны к перпендикуляру; H – перпендикуляр; b и c – стороны, противолежащие углам Y и B соответственно.
Прямоугольный треугольник
Вы могли подумать, что мы забыли о прямоугольных треугольниках, но это не так. Прямоугольный треугольник – треугольник, у которого один из углов равен 90 градусов. Высота в прямоугольном треугольнике только одна, ведь две остальные являются сторонами, а точнее катетами. Единственный перпендикуляр выходит из прямого угла и опускается на гипотенузу. Формул для нахождения для этого случая достаточно много:
- H = ab/c;
- H = ab/√(a2 +b 2);
- H = csinAcosA=c sinBcosB;
- H = bsinA=a sinB;
- H = √de.
где:
H – высота;
a, b – катеты;
с – гипотенуза;
A, B – углы при гипотенузе;
d, e – отрезки, полученные от деления гипотенузы высотой.
Заключение
Так, в этой статье мы рассмотрели определение высоты треугольника. Какие есть типы треугольников? Какие формулы можно использовать для нахождения высоты? Теперь на все эти вопросы вы сможете дать развернутые, а главное правильные ответы.



























