Все что нужно знать о шестиугольной пирамиде

Пирамида - это трехмерная фигура, основание которой представляет собой многоугольник, а боковые стороны являются треугольниками. Шестиугольная пирамида - ее частный вид. Помимо того, существуют другие вариации, когда в основании треугольника (такая фигура называется тетраэдр) находится квадрат, прямоугольник, пятиугольник и так далее по нарастанию. Когда количество точек становится бесконечным, то получается конус.

Шестиугольная пирамида

В целом это одна из последних и самых сложных тем в стереометрии. Изучается где-то в 10-11 классах и рассматривается только вариант, когда в основании находится правильная фигура. Одно из труднейших заданий по ЕГЭ зачастую бывает связано с этим параграфом.

И-так, в основании правильной шестиугольной пирамиды лежит правильный шестиугольник. Что это значит? У фигуры в основании все стороны равны. Боковые же части состоят из равнобедренных треугольников. Вершины их соприкасаются в одной точке. Данная фигура представлена на фото ниже.

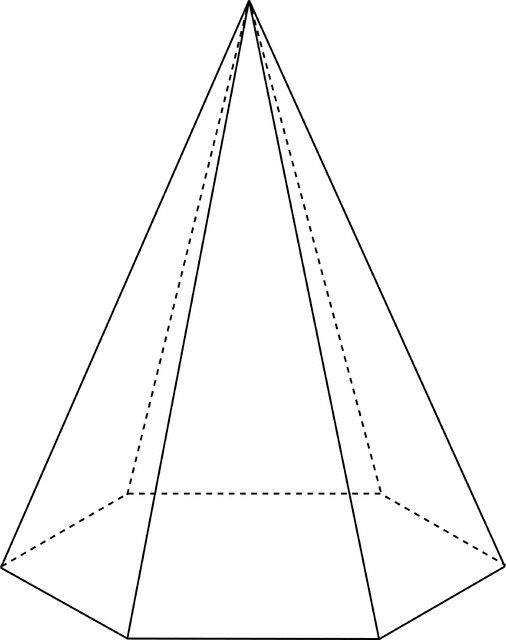
Как найти площадь всей поверхности и объем шестиугольной пирамиды?

В отличие от математики, которую преподают в университетах, школьная наука обучает обходить стороной и упрощать некоторые сложные понятия. Например, если не известно, как найти площадь фигуры, то приходится делить ее на части и уже по известным формулам площадей разделенных фигур находить ответ. Такому принципу нужно последовать и в представленном случае.

То есть, чтобы найти площадь поверхности всей шестиугольной пирамиды, надо найти площадь основания, затем площадь одной из боковых сторон и умножить ее на 6.

Применяются такие формулы:

S (полное) = 6S (боковой стороны) + S (основания) , (1);

S (основания) = 3√3 / 2a² , (2);

6S (боковой стороны) = 6×1 / 2ab = 3ab , (3);

S (полное) = 3ab + (3√3 / 2a²) = 3(2a^2b + √3) / 2a² , (4).

Где S - площадь, см²;

a - длина основания, см;

b - апофема (высота боковой грани), см.

Для того чтобы найти площадь всей поверхности или какой-либо ее составляющей, требуется всего лишь сторона основания шестиугольной пирамиды и апофема. Если в задаче дано это в условии, то решение не должно составить труда.

С объемом дела обстоят намного легче, но чтобы его найти, нужна высота (h) самой шестиугольной пирамиды. Ну и, конечно же, сторона основания, благодаря которой нужно найти ее площадь.

Формула выглядит следующим образом:

V = 1/3 × S (основания) × h , (5).

Где V - объем, см³;

h - высота фигуры, см.

Вариант задачи, который может попасться на экзамене

Условие. Дана правильная шестиугольная пирамида. Длина основания равна 3 см. Высота составляет 5 см. Найти объем данной фигуры.

Решение: V = 1/3 × (3√3/2 × 3²) × 5 = 5/3 × √3/6 = 5√3/18.

Ответ: объем правильной шестиугольной пирамиды составляет 5√3/18 см.