Как вычислить площадь пирамиды: основания, боковую и полную?

При подготовке к ЕГЭ по математике учащимся приходится систематизировать знания по алгебре и геометрии. Хочется объединить все известные сведения, например, о том, как вычислить площадь пирамиды. Причем начиная от основания и боковых граней до площади всей поверхности. Если с боковыми гранями ситуация ясна, так как они являются треугольниками, то основание всегда разное.

Как быть при нахождении площади основания пирамиды?

Оно может быть совершенно любой фигурой: от произвольного треугольника до n-угольника. И это основание, кроме различия в количестве углов, может являться правильной фигурой или неправильной. В интересующих школьников заданиях по ЕГЭ встречаются только задания с правильными фигурами в основании. Поэтому речь будет идти только о них.

Правильный треугольник

То есть равносторонний. Тот, у которого все стороны равны и обозначены буквой «а». В этом случае площадь основания пирамиды вычисляется по формуле:

S = (а² * √3) / 4.

Квадрат

Формула для вычисления его площади самая простая, здесь «а» - снова сторона:

S = а².

Произвольный правильный n-угольник

У стороны многоугольника то же обозначение. Для количества углов используется латинская буква n.

S = (n * а²) / (4 * tg (180º/n)).

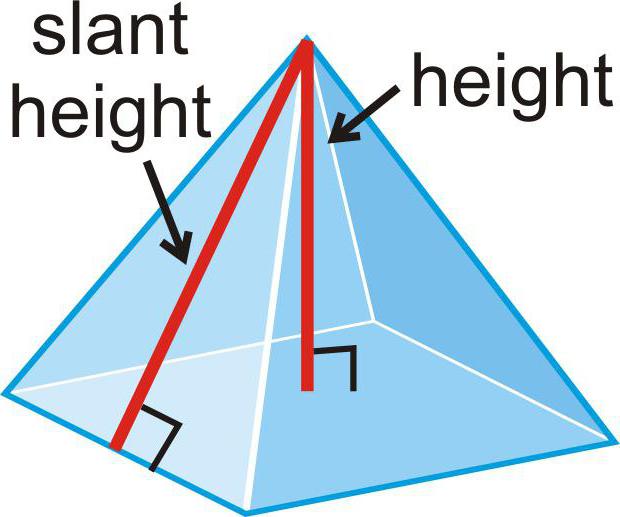
Как поступить при вычислении площади боковой и полной поверхности?

Поскольку в основании лежит правильная фигура, то все грани пирамиды оказываются равными. Причем каждая из них является равнобедренным треугольником, поскольку боковые ребра равны. Тогда для того, чтобы вычислить боковую площадь пирамиды, потребуется формула, состоящая из суммы одинаковых одночленов. Число слагаемых определяется количеством сторон основания.

Площадь равнобедренного треугольника вычисляется по формуле, в которой половина произведения основания умножается на высоту. Эта высота в пирамиде называется апофемой. Ее обозначение - «А». Общая формула для площади боковой поверхности выглядит так:

S = ½ Р*А, где Р — периметр основания пирамиды.

Бывают ситуации, когда не известны стороны основания, но даны боковые ребра (в) и плоский угол при ее вершине (α). Тогда полагается использовать такую формулу, чтобы вычислить боковую площадь пирамиды:

S = n/2 * в² sin α.

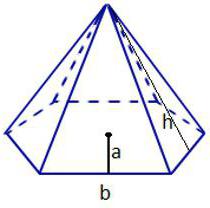
Задача № 1

Условие. Найти общую площадь пирамиды, если в его основании лежит равносторонний треугольник со стороной 4 см, а апофема имеет значение √3 см.

Решение. Его начинать нужно с расчета периметра основания. Поскольку это правильный треугольник, то Р = 3*4 = 12 см. Поскольку апофема известна, то можно сразу вычислить площадь всей боковой поверхности: ½*12*√3 = 6√3 см².

Для треугольника в основании получится такое значение площади: (4²*√3) / 4 = 4√3 см².

Для определения всей площади потребуется сложить два получившихся значения: 6√3 + 4√3 = 10√3 см².

Ответ. 10√3 см².

Задача № 2

Условие. Имеется правильная четырехугольная пирамида. Длина стороны основания равна 7 мм, боковое ребро — 16 мм. Необходимо узнать площадь ее поверхности.

Решение. Поскольку многогранник — четырехугольный и правильный, то в его основании лежит квадрат. Узнав площади основания и боковых граней, удастся сосчитать площадь пирамиды. Формула для квадрата дана выше. А у боковых граней известны все стороны треугольника. Поэтому можно использовать формулу Герона для вычисления их площадей.

Первые расчеты просты и приводят к такому числу: 49 мм². Для второго значения потребуется вычислить полупериметр: (7 + 16*2):2 = 19,5 мм. Теперь можно вычислять площадь равнобедренного треугольника: √(19,5*(19,5-7)*(19,5-16)²) = √2985,9375 = 54,644 мм². Таких треугольников всего четыре, поэтому при подсчете итогового числа потребуется его умножить на 4.

Получается: 49 + 4*54,644 = 267,576 мм².

Ответ. Искомое значение 267,576 мм².

Задача № 3

Условие. У правильной четырехугольной пирамиды необходимо вычислить площадь. В ней известна сторона квадрата — 6 см и высота — 4 см.

Решение. Проще всего воспользоваться формулой с произведением периметра и апофемы. Первое значение найти просто. Второе немного сложнее.

Придется вспомнить теорему Пифагора и рассмотреть прямоугольный треугольник. Он образован высотой пирамиды и апофемой, которая является гипотенузой. Второй катет равен половине стороны квадрата, поскольку высота многогранника падает в его середину.

Искомая апофема (гипотенуза прямоугольного треугольника) равна √(3² + 4²) = 5 (см).

Теперь можно вычислять искомую величину: ½*(4*6)*5+6² = 96 (см²).

Ответ. 96 см².

Задача № 4

Условие. Дана правильная шестиугольная пирамида. Стороны ее основания равны 22 мм, боковые ребра — 61 мм. Чему равна площадь боковой поверхности этого многогранника?

Решение. Рассуждения в ней такие же, как были описаны в задаче №2. Только там была дана пирамида с квадратом в основании, а теперь это шестиугольник.

Первым делом вычисляется площадь основания по указанной выше формуле: (6*22²) / (4*tg (180º/6)) = 726/(tg30º) = 726√3 см².

Теперь необходимо узнать полупериметр равнобедренного треугольника, который является боковой гранью. (22+61*2):2 = 72 см. Осталось по формуле Герона сосчитать площадь каждого такого треугольника, а потом умножить ее на шесть и сложить с той, что получилась для основания.

Расчеты по формуле Герона: √(72*(72-22)*(72-61)²)=√435600=660 см². Вычисления, которые дадут площадь боковой поверхности: 660*6 = 3960 см². Осталось их сложить, чтобы узнать всю поверхность: 5217,47≈5217 см².

Ответ. Основания - 726√3 см², боковой поверхности - 3960 см², вся площадь - 5217 см².