Стереометрия, как раздел геометрии в пространстве, изучает свойства призм, цилиндров, конусов, шаров, пирамид и других объемных фигур. Данная статья посвящена подробному рассмотрению характеристик и свойств шестиугольной правильной пирамиды.
Какая пирамида будет изучаться
Правильная шестиугольная пирамида представляет собой фигуру в пространстве, которая ограничена одним равносторонним и равноугольным шестиугольником, и шестью одинаковыми треугольниками равнобедренными. Эти треугольники могут быть также равносторонними при определенных условиях. Эта пирамида ниже показана.
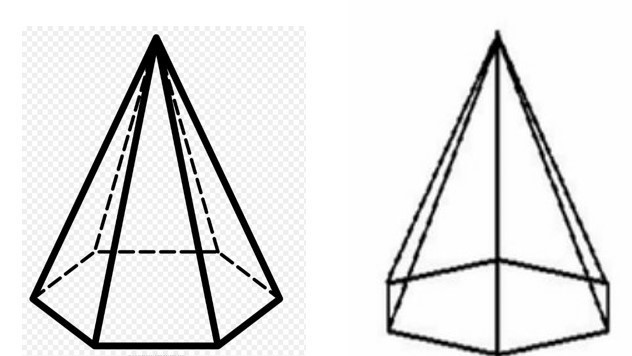
Здесь изображена одна и та же фигура, только в одном случае она повернута боковой гранью к читателю, а в другом - боковым ребром.
Правильная шестиугольная пирамида имеет 7 граней, которые были названы выше. Также ей принадлежат 7 вершин и 12 ребер. В отличие от призм, у всех пирамид имеется одна особая вершина, которая образована пересечением боковых треугольников. Для правильной пирамиды она играет важную роль, поскольку опущенный с нее на основание фигуры перпендикуляр является высотой. Далее высоту будем обозначать буквой h.
Показанная пирамида называется правильной по двум причинам:
- в ее основании находится шестиугольник с равными длинами сторон a и с одинаковыми углами по 120o;
- высота пирамиды h пересекает шестиугольник точно в его центре (точка пересечения лежит на одинаковом расстоянии от всех сторон и от всех вершин шестиугольника).
Площадь поверхности
Свойства правильной пирамиды шестиугольной начнем рассматривать с определения ее площади. Для этого сначала полезно привести развертку фигуры на плоскости. Схематическое ее изображение показано ниже.
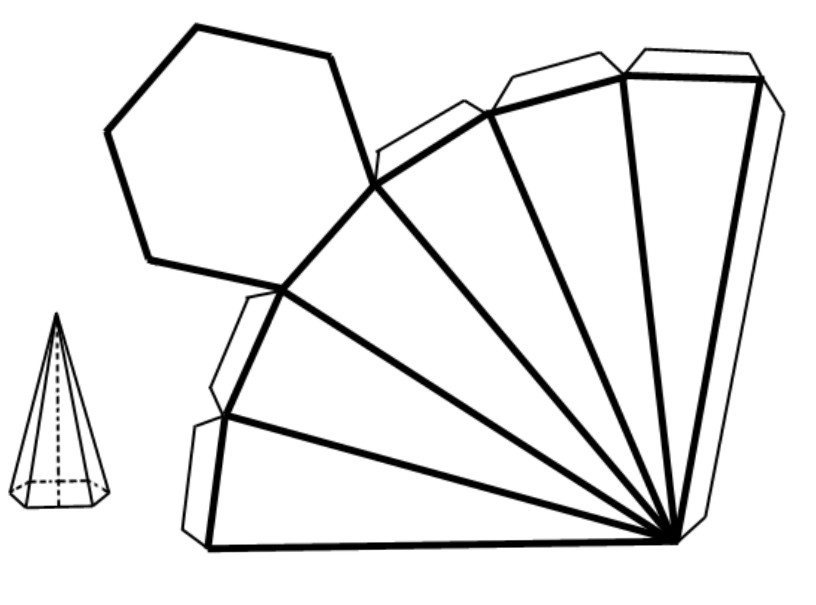
Видно, что площадь развертки, а значит, и всей поверхности рассматриваемой фигуры, равна сумме площадей шести одинаковых треугольников и одного шестиугольника.
Для определения площади шестиугольника S6 воспользуемся универсальной формулой для правильного n-угольника:
Sn = n/4*a2*ctg(pi/n) =>
S6 = 3*√3/2*a2.
Где буквой a обозначена длина стороны шестиугольника.
Площадь треугольника S3 боковой стороны найти можно, если знать величину его высоты hb:
S3 = 1/2*hb*a.
Поскольку все шесть треугольников равны между собой, то получаем рабочее выражение для определения площади шестиугольной пирамиды с правильным основанием:
S = S6 + 6*S3 = 3*√3/2*a2 + 6*1/2*hb*a = 3*a*(√3/2*a + hb).
Объем пирамиды
Так же, как и площадь, объем шестиугольной правильной пирамиды является важным ее свойством. Этот объем рассчитывается по общей формуле для всех пирамид и конусов. Запишем ее:
V = 1/3*So*h.
Здесь символом So названа площадь шестиугольного основания, то есть So = S6.
Подставляя в формулу для V записанное выше выражение для S6, приходим к конечному равенству для определения объема пирамиды шестиугольной правильной:
V = √3/2*a2 *h.
Пример геометрической задачи
В шестиугольной пирамиде правильной боковое ребро в два раза больше длины стороны основания. Зная, что последнее равно 7 см, необходимо вычислить площадь поверхности и объем данной фигуры.
Как можно догадаться, решение этой задачи предполагает использование полученных выше выражений для S и V. Тем не менее сразу ими воспользоваться не получится, поскольку мы не знаем апофему и высоту правильной пирамиды шестиугольной. Займемся их вычислением.
Апофему hb можно определить, рассмотрев треугольник прямоугольный, построенный на сторонах b, a/2 и hb. Здесь b - длина бокового ребра. Используя условие задачи, получаем:
hb = √(b2-a2/4) = √(142-72/4) = 13,555 см.
Высоту h пирамиды определить можно точно так же, как апофему, только рассматривать теперь следует треугольник со сторонами h, b и a, находящийся внутри пирамиды. Высота будет равна:
h = √(b2 - a2) = √(142 - 72) = 12,124 см.
Видно, что рассчитанное значение высоты меньше такового для апофемы, что справедливо для любой пирамиды.
Теперь можно воспользоваться выражениями для объема и площади:
S = 3*a*(√3/2*a + hb) = 3*7*(√3/2*7 + 13,555) = 411,96 см2;
V = √3/2*a2*h = √3/2*72*12,124 = 514,48 см3.
Таким образом, для однозначного определения любой характеристики правильной шестиугольной пирамиды необходимо знать два любых ее линейных параметра.
























