Импульс частицы и механической системы - определение и особенности

Многие задачи на движение в классической механике могут быть решены с использованием понятия импульса частицы или всей механической системы. Рассмотрим подробнее концепцию импульса, а также покажем, как полученные знания можно использовать для решения физических задач.

Главная характеристика движения

В XVII веке при изучении перемещения небесных тел в пространстве (вращение планет в нашей Солнечной системе) Исаак Ньютон использовал концепцию количества движения. Справедливости ради отметим, что несколькими десятками лет ранее подобную характеристику уже применял Галилео Галилей при описании тел в движении. Однако только Ньютон смог ее лаконично встроить в разработанную им классическую теорию перемещения небесных тел.

Все знают, что одной из важных величин, характеризующих быстроту изменения координат тела в пространстве, является скорость. Если ее умножить на массу движущегося объекта, то мы получим упомянутое количество движения, то есть справедлива следующая формула:

p¯ = m*v¯

Как видно, p¯ - это векторная величина, направление которой совпадает с таковым для скорости v¯. Измеряется она в кг*м/с.

Физический смысл p¯ можно понять на следующем простом примере: с одинаковыми скоростями едет грузовик и летит муха, ясно, что остановить грузовик человек не сможет, а вот муху сможет без проблем. То есть количество движения прямо пропорционально не только скорости, но и массе тела (зависит от инерционных свойств).

Движение материальной точки или частицы

При рассмотрении многих задач на движение размеры и форма перемещающегося объекта часто не играют существенной роли для их решения. В этом случае вводят одно из самых распространенных приближений - тело считают частицей или материальной точкой. Она представляет собой безмерный объект, вся масса которого сосредоточена в центре тела. Это удобное приближение справедливо, когда размеры тела намного меньше проходимых им расстояний. Яркий пример - движение автомобиля между городами, вращение нашей планеты по своей орбите.

Таким образом, состояние рассматриваемой частицы характеризуется массой и скоростью ее перемещения (заметим, что скорость может зависеть от времени, то есть не быть постоянной).

Что это - импульс частицы?

Часто под этими словами понимают количество движения материальной точки, то есть величину p¯. Это не совсем правильно. Разберемся в этом вопросе подробнее, для этого запишем второй закон Исаака Ньютона, который проходят уже в 7 классе школы, имеем:

F¯ = m*a¯

Зная, что ускорение - это скорость изменения величины v¯ во времени, перепишем ее следующим образом:

F¯ = m*dv¯/dt => F¯*dt = m*dv¯

Если действующая сила не будет меняться со временем, тогда для интервала Δt будет справедливо равенство:

F¯*Δt = m*Δv¯ = Δp¯

Левая часть этого равенства (F¯*Δt) называется импульсом силы, правая часть (Δp¯) - изменение количества движения. Поскольку рассматривается случай движения материальной точки, то можно это выражение назвать формулой импульса частицы. Она показывает, на сколько изменится ее полное количество движения за время Δt при действии соответствующего импульса силы.

Момент импульса

Разобравшись с понятием импульса частицы массой m для линейного движения, перейдем к рассмотрению аналогичной характеристики для кругового перемещения. Если материальная точка, имея импульс p¯, вращается вокруг оси O на расстоянии от нее r¯, тогда можно записать такое выражение:

L¯ = r¯*p¯

Это выражение представляет собой момент импульса частицы, который так же, как и p¯, является величиной векторной (L¯ направлен согласно правилу правой руки перпендикулярно плоскости, построенной на отрезках r¯ и p¯).

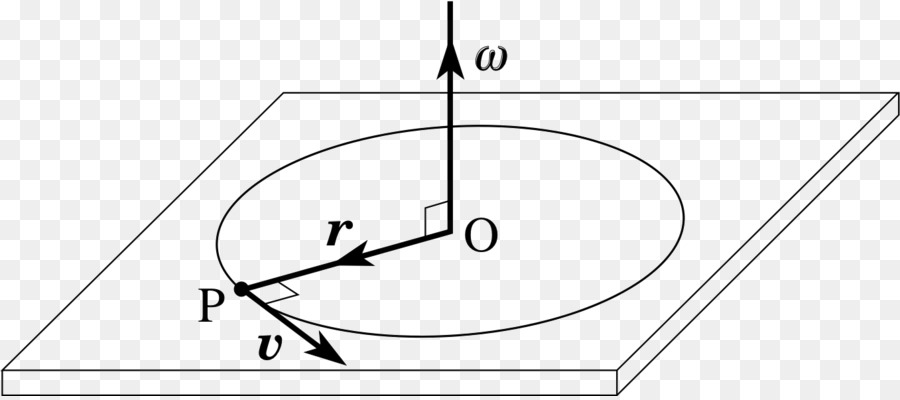
Если импульс p¯ характеризует интенсивность линейного перемещения тела, то L¯ имеет аналогичный физический смысл только для круговой траектории (вращение вокруг оси).

Формула для момента импульса частицы, записанная выше, в этом виде не используется для решения задач. Путем несложных математических преобразований можно прийти к следующему выражению:

L¯ = I*ω¯

Где ω¯ - угловая скорость, I - момент инерции. Эта запись подобна таковой для линейного импульса частицы (аналогия между ω¯ и v¯ и между I и m).

Законы сохранения величин p¯ и L¯

В третьем пункте статьи было введено понятие импульса внешней силы. Если такие силы не действуют на систему (она является закрытой, и в ней имеют место лишь внутренние силы), то суммарный импульс частиц, принадлежащих системе, остается величиной постоянной, то есть:

p¯ = const

Заметим, что в результате внутренних взаимодействий сохраняется каждая координата импульса:

p_x = const.; p_y = const.; p_z = const

Обычно этот закон используют для решения проблем со столкновением твердых тел, например шаров. Важно знать, что какой бы характер не имело столкновение (абсолютно упругое или пластическое), общее количество движения всегда будет оставаться одним и тем же до удара и после него.

Проводя полную аналогию с линейным движением точки, закон сохранения для момента импульса запишем так:

L¯ = const. или I₁*ω₁¯ = I₂*ω₂¯

То есть любые внутренние изменения момента инерции системы ведут к пропорциональному изменению угловой скорости ее вращения.

Пожалуй, одним из распространенных явлений, демонстрирующих этот закон, является вращение фигуриста на льду, когда он группирует по разному свое тело, изменяя при этом свою угловую скорость.

Задача на столкновение двух липких шаров

Рассмотрим пример решения задачи на сохранение линейного импульса частиц, движущихся друг навстречу другу. Пусть этими частицами будут шары, имеющие липкую поверхность (в данном случае шар можно считать материальной точкой, поскольку его размеры не влияют на решение поставленной проблемы). Итак, один шар движется вдоль положительного направления оси X со скоростью 5 м/с, он имеет массу 3 кг. Второй шар движется вдоль отрицательного направления оси X, его скорость и масса равны 2 м/с и 5 кг соответственно. Необходимо определить, в каком направлении и с какой скоростью будет перемещаться система после столкновения шаров и их прилипания друг к другу.

Импульс системы до столкновения определяется разностью количества движения для каждого шара (разность берется потому, что тела направлены в разные стороны). После же столкновения импульс p¯ выражен лишь одной частицей, масса которой равна m₁ + m₂. Поскольку шары движутся только вдоль оси X, имеем выражение:

m₁*v₁ - m₂*v₂ = (m₁+m₂)*u

Откуда неизвестная скорость находится по формуле:

u = (m₁*v₁ - m₂*v₂)/(m₁+m₂)

Подставляя данные из условия, получаем ответ: u = 0,625 м/c. Положительное значение скорости говорит о том, что система после удара будет двигаться по направлению оси X, а не против него.