Каждый школьник слышал о круглом конусе и представляет, как выглядит эта объемная фигура. В данной статье дается определение развертки конуса, приводятся формулы, описывающие ее характеристики, а также описывается способ ее построения с помощью циркуля, транспортира и линейки.
Круглый конус в геометрии
Приведем геометрическое определение этой фигуры. Круглым конусом называется поверхность, которая образована прямыми отрезками, соединяющими все точки некоторой окружности с одной-единственной точкой пространства. Эта единственная точка не должна принадлежать плоскости, в которой лежит окружность. Если вместо окружности взять круг, то указанный способ также приводит к получению конуса.
Круг называется основанием фигуры, его окружность - это директриса. Отрезки, соединяющие точку с директрисой, называются генератрисами или образующими, а точка, где они пересекаются - это вершина конуса.
Круглый конус может быть прямым и наклонным. Обе фигуры показаны ниже на рисунке.
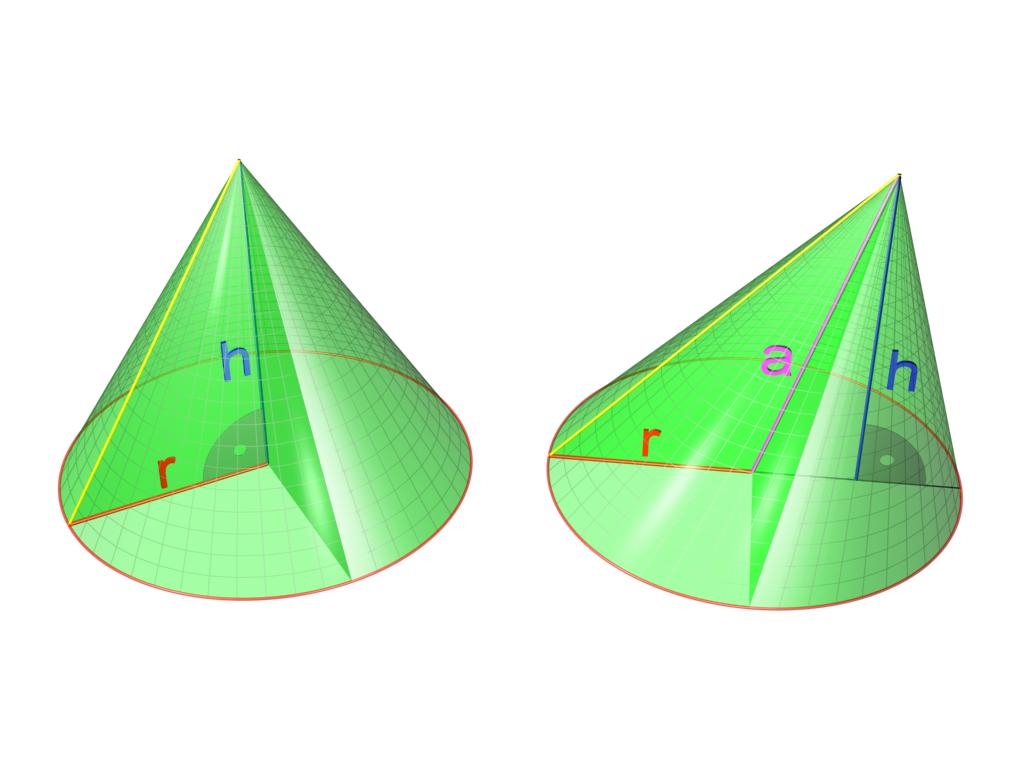
Разница между ними заключается в следующем: если перпендикуляр из вершины конуса падает точно в центр окружности, то конус будет прямым. Для него перпендикуляр, который называется высотой фигуры, является частью его оси. В случае конуса наклонного высота и ось образуют некоторый острый угол.
Ввиду простоты и симметричности фигуры далее будем рассматривать свойства только прямого конуса с круглым основанием.
Получение фигуры с помощью вращения
Перед тем как перейти к рассмотрению развертки поверхности конуса, полезно узнать, как с помощью вращения можно получить эту пространственную фигуру.
Предположим, что у нас имеется прямоугольный треугольник со сторонами a, b, c. Первые две из них являются катетами, c - это гипотенуза. Поставим треугольник на катет a и начнем его вращать вокруг катета b. Гипотенуза c при этом опишет коническую поверхность. Эта простая методика получения конуса изображена ниже на схеме.

Очевидно, что катет a будет радиусом основания фигуры, катет b - его высотой, а гипотенуза c соответствует образующей круглого прямого конуса.
Вид развертки конуса
Как можно догадаться, конус образован двумя типами поверхностей. Одна из них - это плоский круг основания. Предположим, что он имеет радиус r. Вторая поверхность является боковой и называется конической. Пусть ее образующая будет равна g.
Если у нас имеется бумажный конус, то можно взять ножницы и отрезать от него основание. Затем, коническую поверхность следует разрезать вдоль любой образующей и развернуть ее на плоскости. Таким способом мы получили развертку боковой поверхности конуса. Две поверхности вместе с исходным конусом показаны на схеме ниже.

Внизу справа изображен круг основания. По центру показана развернутая коническая поверхность. Оказывается, что она соответствует некоторому круговому сектору круга, радиус которого равен длине образующей g.
Угол и площадь развертки
Теперь получим формулы, которые по известным параметрам g и r позволяют рассчитать площадь и угол развертки конуса.
Очевидно, что дуга кругового сектора, показанного выше на рисунке, имеет длину, равную длине окружности основания, то есть:
l = 2*pi*r.
Если бы весь круг радиусом g был построен, то его бы длина составила:
L = 2*pi*g.
Поскольку длина L соответствует 2*pi радианам, тогда угол, на который опирается дуга l, можно определить из соответствующей пропорции:
L ==> 2*pi;
l ==> φ.
Тогда неизвестный угол φ будет равен:
φ = 2*pi*l/L.
Подставляя выражения для длин l и L, приходим к формуле для угла развертки боковой поверхности конуса:
φ = 2*pi*r/g.
Угол φ здесь выражен в радианах.
Для определения площади Sb кругового сектора воспользуемся найденным значением φ. Составляем еще одну пропорцию, только уже для площадей. Имеем:
2*pi ==> pi*g2;
φ ==> Sb.
Откуда следует выразить Sb, а затем, подставить значение угла φ. Получаем:
Sb = φ*g2*pi/(2*pi) = 2*pi*r/g*g2/2 = pi*r*g.
Для площади конической поверхности мы получили достаточно компактную формулу. Величина Sb равна произведению трех множителей: числа пи, радиуса фигуры и ее образующей.
Тогда площадь всей поверхности фигуры будет равна сумме Sb и So (площадь круглого основания). Получаем формулу:
S = Sb + So = pi*r*(g + r).
Построение развертки конуса на бумаге

Для выполнения этой задачи понадобится лист бумаги, карандаш, транспортир, линейка и циркуль.
В первую очередь начертим прямоугольный треугольник со сторонами 3 см, 4 см и 5 см. Его вращение вокруг катета в 3 см даст искомый конус. У фигуры r = 3 см, h = 4 см, g = 5 см.
Построение развертки начнем с рисования циркулем окружности радиусом r. Ее длина будет равна 6*pi см. Теперь рядом с ней нарисуем еще одну окружность, но уже радиусом g. Ее длина будет соответствовать 10*pi см. Теперь нам нужно от большой окружности отрезать круговой сектор. Его угол φ равен:
φ = 2*pi*r/g = 2*pi*3/5 = 216o.
Теперь откладываем транспортиром этот угол на окружности с радиусом g и проводим два радиуса, которые будут ограничивать круговой сектор.
Таким образом, мы построили развертку конуса с указанными параметрами радиуса, высоты и образующей.
Пример решения геометрической задачи

Дан круглый прямой конус. Известно, что угол его боковой развертки равен 120o. Необходимо найти радиус и образующую этой фигуры, если известно, что высота h конуса равна 10 см.
Задача не является сложной, если вспомнить, что круглый конус - это фигура вращения прямоугольного треугольника. Из этого треугольника следует однозначная связь между высотой, радиусом и образующей. Запишем соответствующую формулу:
g2 = h2 + r2.
Вторым выражением, которое следует использовать при решении, является формула для угла φ:
φ = 2*pi*r/g.
Таким образом, мы имеем два уравнения, связывающих две неизвестные величины (r и g).
Выражаем из второй формулы g и подставляем результат в первую, получаем:
g = 2*pi*r/φ;
h2 + r2 = 4*pi2*r2/φ2 =>
r = h /√(4*pi2/φ2 - 1).
Угол φ = 120o в радианах равен 2*pi/3. Подставляем это значение, получаем конечные формулы для r и g:
r = h /√8;
g =3*h /√8.
Остается подставить значение высоты и получить ответ на вопрос задачи: r ≈ 3,54 см, g ≈ 10,61 см.



























