Изучение свойств пространственных фигур играет важную роль для решения практических задач. Наука, которая занимается фигурами в пространстве, называется стереометрией. В данной статье, с точки зрения стереометрии, рассмотрим конус и покажем, как находить площадь конуса.
Конус с круглым основанием
В общем случае конусом называется поверхность, построенная на некоторой плоской кривой, все точки которой соединены отрезками с одной точкой пространства. Последняя называется вершиной конуса.
Из приведенного определения понятно, что кривая может иметь произвольную форму, например параболическую, гиперболическую, эллиптическую и так далее. Тем не менее на практике и в задачах по геометрии встречается часто именно круглый конус. Он показан ниже на рисунке.
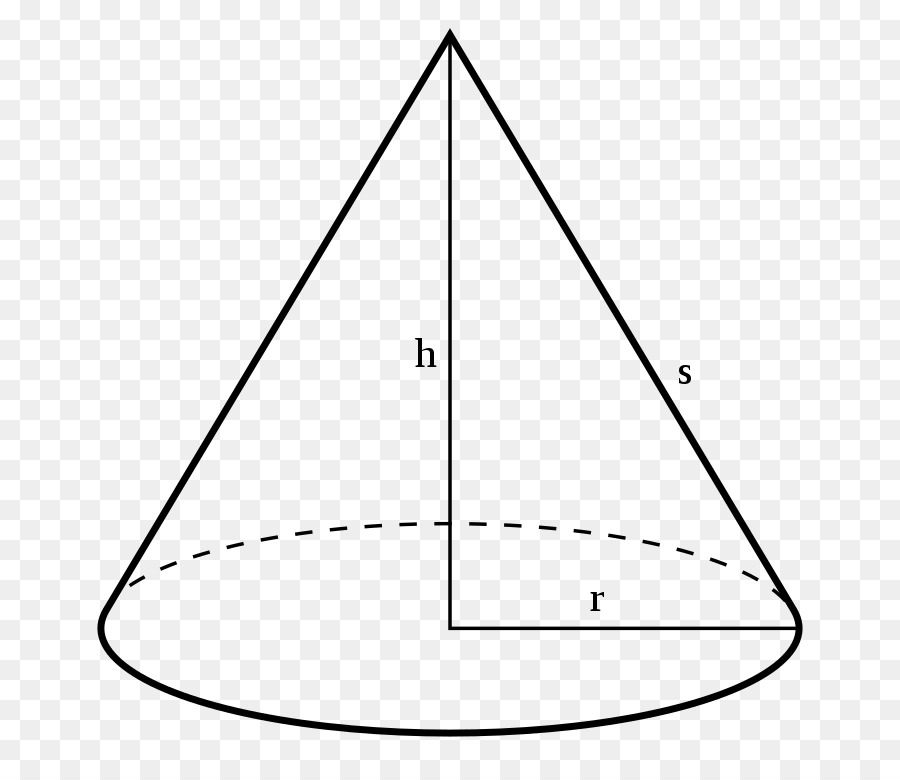
Здесь символом r обозначен радиус круга, находящегося в основании фигуры, h - это перпендикуляр к плоскости круга, который проведен из вершины фигуры. Он называется высотой. Величина s - это образующая конуса, или его генератриса.
Видно, что отрезки r, h и s образуют прямоугольный треугольник. Если его вращать вокруг катета h, то гипотенуза s опишет коническую поверхность, а катет r образует круглое основание фигуры. По этой причине конус считают фигурой вращения. Три названных линейных параметра связаны между собой равенством:
s2 = r2 + h2
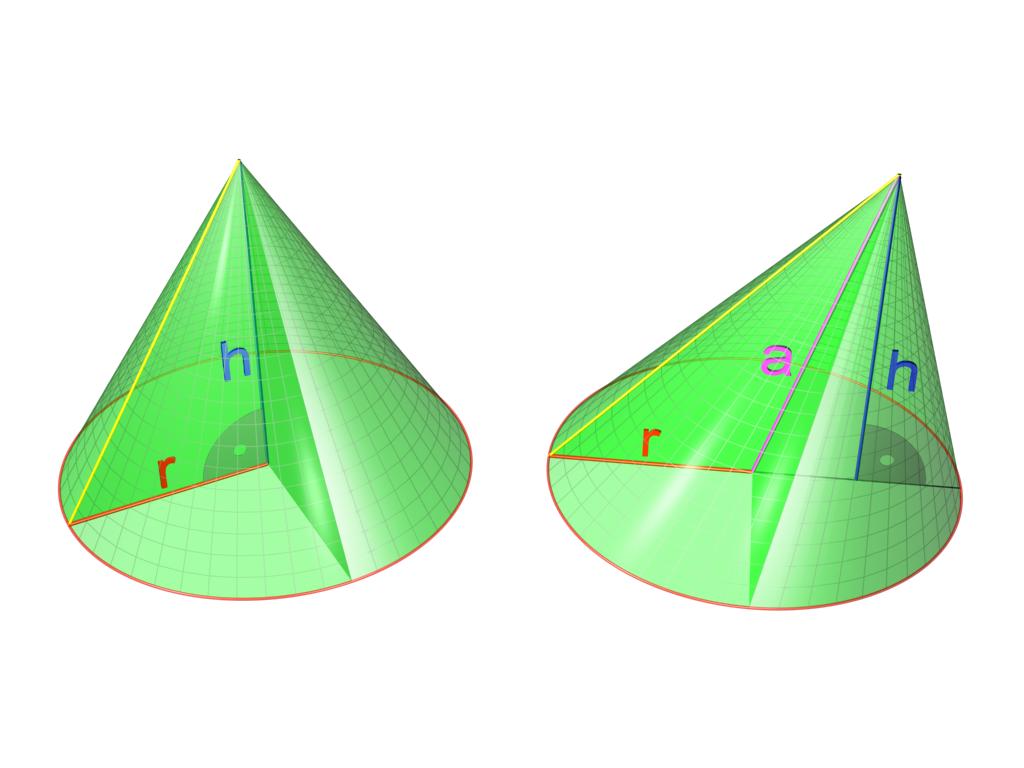
Отметим, что приведенное равенство справедливо только для круглого прямого конуса. Прямой фигура является только в том случае, если ее высота падает точно в центр круга основания. Если это условие не выполняется, то фигура называется наклонной. Разница между прямым и наклонным конусами показана ниже на рисунке.
Развертка фигуры
Изучение площади поверхности конуса удобно проводить, рассматривая его на плоскости. Такой способ представления поверхности фигур в пространстве называется их разверткой. Для конуса эту развертку можно получить следующим образом: необходимо взять фигуру, изготовленную, например, из бумаги. Затем, ножницами отрезать круглое основание по окружности. После этого вдоль генератрисы сделать разрез конической поверхности и развернуть ее на плоскость. Результатом этих несложных операций будет развертка конуса, показанная ниже на рисунке.
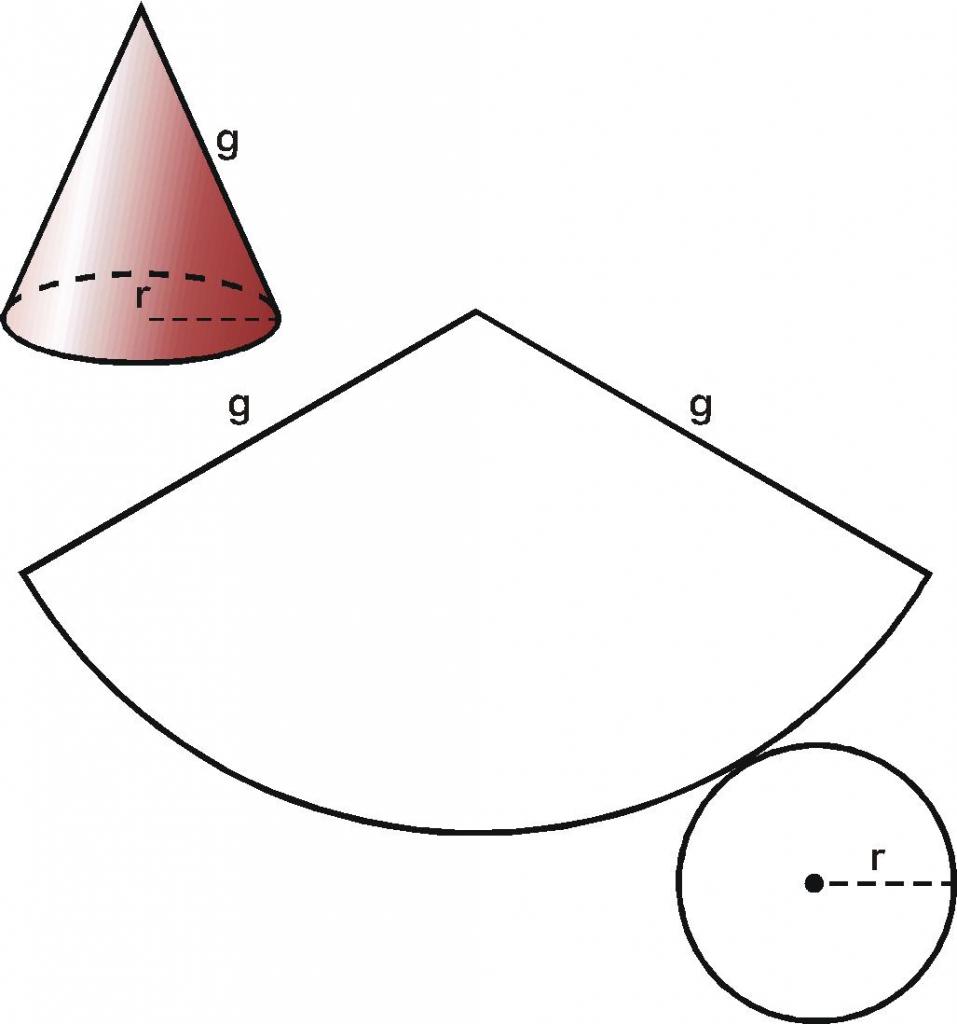
Как видно, поверхность конуса действительно можно представить на плоскости. Она состоит из двух следующих частей:
- круг радиусом r, представляющий основание фигуры;
- круговой сектор радиусом g, являющийся конической поверхностью.
Формула площади конуса предполагает нахождение площадей обеих развернутых поверхностей.
Вычисление площади поверхности фигуры
Разделим поставленную задачу на два этапа. Сначала найдем площадь основания конуса, затем площадь конической поверхности.
Первую часть задачи решить просто. Поскольку дан радиус r, то для вычисления площади основания достаточно вспомнить соответствующее выражение для площади круга. Запишем его:
So = pi × r2
Если радиус не известен, тогда сначала следует его найти, пользуясь формулой связи между ним, высотой и генератрисой.
Вторая часть задачи по нахождению площади конуса несколько сложнее. Заметим, что круговой сектор построен на радиусе g генератрисы и ограничен дугой, длина которой равна длине окружности круга. Этот факт позволяет записать пропорцию и найти угол рассматриваемого сектора. Обозначим его греческой буквой φ. Этот угол будет равен:
2 × pi => 2 × pi × g;
φ => 2 × pi × r;
φ = 2 × pi × r / g
Зная центральный угол φ кругового сектора, можно с помощью соответствующей пропорции найти его площадь. Обозначим ее символом Sb. Она будет равна:
2 × pi => pi × g2;
φ => Sb;
Sb = pi × g2 × φ / (2 × pi) = pi × r × g
То есть площадь конической поверхности соответствует произведению образующей g, радиуса основания r и числа Пи.
Зная, чему равны площади обеих рассмотренных поверхностей, можно записать конечную формулу площади конуса:
S = So + Sb = pi × r2 + pi × r × g = pi × r × (r + g)
Записанное выражение предполагает для вычисления S знание двух линейных параметров конуса. Если g или r неизвестны, то их можно найти через высоту h.
Задача на вычисление площади конуса
Известно, что высота круглого прямого конуса равна его диаметру. Необходимо вычислить площадь фигуры, зная, что площадь ее основания составляет 50 см2.
Зная площадь круга, можно найти радиус фигуры. Имеем:
So = pi × r2 =>
r = √(So / pi)
Теперь найдем генератрису g через h и r. Согласно условию, высота h фигуры равна двум радиусам r, тогда:
h = 2 × r;
g2 = (2 × r)2 + r2 =>
g = √5 × r = √(5 × So / pi)
Найденные формулы для g и r следует подставить в выражение для всей площади конуса. Получаем:
S = So + pi × √(So / pi) × √(5 × So / pi) = So × (1 + √5)
В полученное выражение подставляем площадь основания So и записываем ответ: S ≈ 161,8 см2.



























