Тангенциальное и нормальное ускорение. Касательное и нормальное ускорение

Изучение физики начинают с рассмотрения механического движения. В общем случае тела движутся по кривым траекториям с переменными скоростями. Для их описания используют понятие ускорения. В данной статье рассмотрим, что такое тангенциальное и нормальное ускорение.

Кинематические величины. Скорость и ускорение в физике

Кинематика механического движения - это раздел физики, который занимается изучением и описанием перемещения тел в пространстве. Кинематика оперирует тремя главными величинами:

• пройденный путь;
• скорость;
• ускорение.

В случае движения по окружности используют аналогичные кинематические характеристики, которые приведены к центральному углу окружности.

С понятием скорости знаком каждый. Она показывает быстроту изменения координат тел, находящихся в движении. Скорость всегда направлена по касательной к линии, вдоль которой тело перемещается (траектории). Далее линейную скорость будем обозначать v¯, а угловую скорость - ω¯.

Ускорение - это скорость изменения величин v¯ и ω¯. Ускорение - это тоже векторная величина, однако ее направление совершенно не зависит от вектора скорости. Ускорение всегда направлено в сторону действующей на тело силы, которая вызывает изменение вектора скорости. Ускорение для любого типа движения можно рассчитать по формуле:

a¯ = dv¯ / dt

Чем сильнее изменится скорость за интервал времени dt, тем больше будет ускорение.

Для понимания изложенной дальше информации необходимо помнить, что ускорение появляется в результате любого изменения скорости, включая изменения как ее модуля, так и ее направления.

Касательное и нормальное ускорение

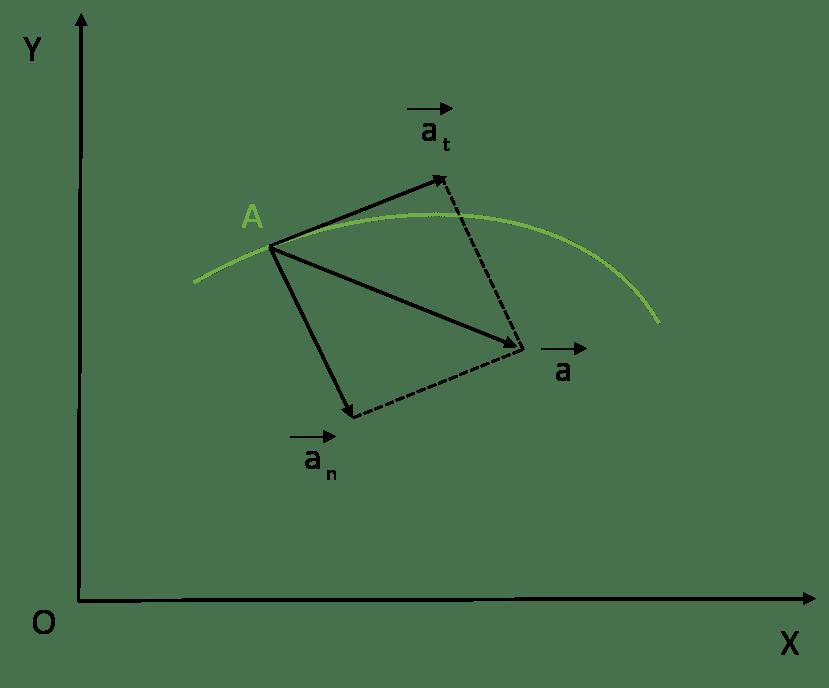
Предположим, что материальная точка движется по некоторой кривой линии. Известно, что в некоторый момент времени t ее скорость была равна v¯. Поскольку скорость - это касательный к траектории вектор, ее можно представить в следующем виде:

v¯ = v × u_t¯

Здесь v - длина вектора v¯, а u_t¯ - единичный вектор скорости.

Чтобы вычислить вектор полного ускорения в момент времени t, необходимо найти производную скорости по времени. Имеем:

a¯ = dv¯ / dt = d (v × u_t¯) / dt

Поскольку модуль скорости и единичный вектор изменяются со временем, то, пользуясь правилом нахождения производной от произведения функций, получаем:

a¯ = dv / dt × u_t¯ + d (u_t¯) / dt × v

Первое слагаемое в формуле называется тангенциальной, или касательной компонентой ускорения, второе слагаемое - это нормальное ускорение.

Касательное ускорение

Еще раз запишем формулу для вычисления касательного ускорения:

a_t¯ = dv / dt × u_t¯

Это равенство означает, что тангенциальное (касательное) ускорение направлено так же, как вектор скорости в любой точке траектории. Оно численно определяет изменение модуля скорости. Например, в случае прямолинейного движения полное ускорение состоит только из касательной составляющей. Нормальное ускорение при таком типе перемещения равно нулю.

Причиной появления величины a_t¯ является воздействие внешней силы на движущееся тело.

В случае вращения с постоянным угловым ускорением α тангенциальная составляющая ускорения может быть вычислена по следующей формуле:

a_t = α × r

Здесь r - это радиус вращения рассматриваемой материальной точки, для которой вычисляется величина a_t.

Нормальное или центростремительное ускорение

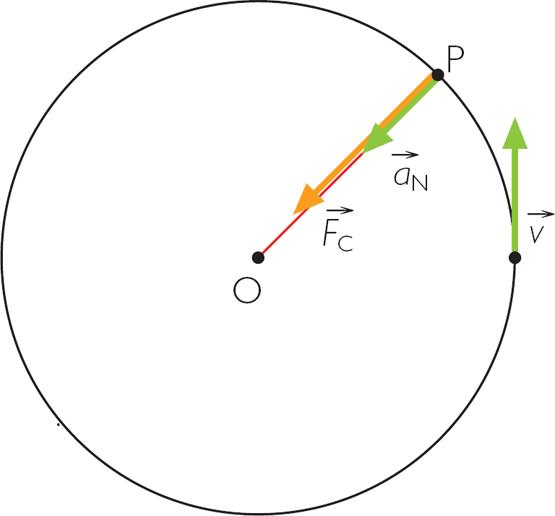
Теперь выпишем еще раз вторую компоненту полного ускорения:

a_c¯ = d (u_t¯) / dt × v

Из геометрических соображений можно показать, что производная единичного касательного к траектории вектора по времени равна отношению модуля скорости v к радиусу r в момент времени t. Тогда выражение выше запишется так:

a_c = v² / r

Эта формула нормального ускорения свидетельствует, что оно, в отличие от касательной компоненты, не зависит от изменения скорости, а определяется квадратом модуля самой скорости. Также a_c возрастает с уменьшением радиуса вращения при постоянной величине v.

Нормальное ускорение называют центростремительным потому, что оно направлено от центра масс вращающегося тела к оси вращения.

Причиной появления этого ускорения является центральная компонента воздействующей на тело силы. Например, в случае вращения планет вокруг нашего Солнца центростремительной силой является гравитационное притяжение.

Нормальное ускорение тела изменяет только направление скорости. Оно не способно изменить ее модуль. Этот факт является важным его отличием от касательной компоненты полного ускорения.

Поскольку центростремительное ускорение возникает всегда, когда вектор скорости поворачивается, то оно существует также в случае равномерного вращения по окружности, при котором тангенциальное ускорение равно нулю.

На практике ощутить на себе влияние нормального ускорения можно, если находиться в машине, когда она совершает затяжной поворот. В этом случае пассажиров прижимает к противоположной направлению поворота двери автомобиля. Это явление - результат действия двух сил: центробежной (смещение пассажиров со своих мест) и центростремительной (давление на пассажиров со стороны двери автомобиля).

Модуль и направление полного ускорения

Итак, мы выяснили, что тангенциальная компонента рассматриваемой физической величины направлена по касательной к траектории движения. В свою очередь, нормальная компонента перпендикулярна траектории в данной точке. Это означает, что две компоненты ускорения перпендикулярны друг другу. Их векторное сложение дает вектор полного ускорения. Вычислить его модуль можно по следующей формуле:

a = √(a_t² + a_c²)

Направление вектора a¯ можно определить как относительно вектора a_t¯, так и относительно a_c¯. Для этого следует использовать соответствующую тригонометрическую функцию. Например, угол между полным и нормальным ускорениями равен:

φ = arccos(a_c / a)

Решение задачи на определение центростремительного ускорения

Колесо, которое имеет радиус 20 см, раскручивается с угловым ускорением 5 рад/с² в течение 10 секунд. Необходимо определить нормальное ускорение точек, находящихся на периферии колеса, через указанное время.

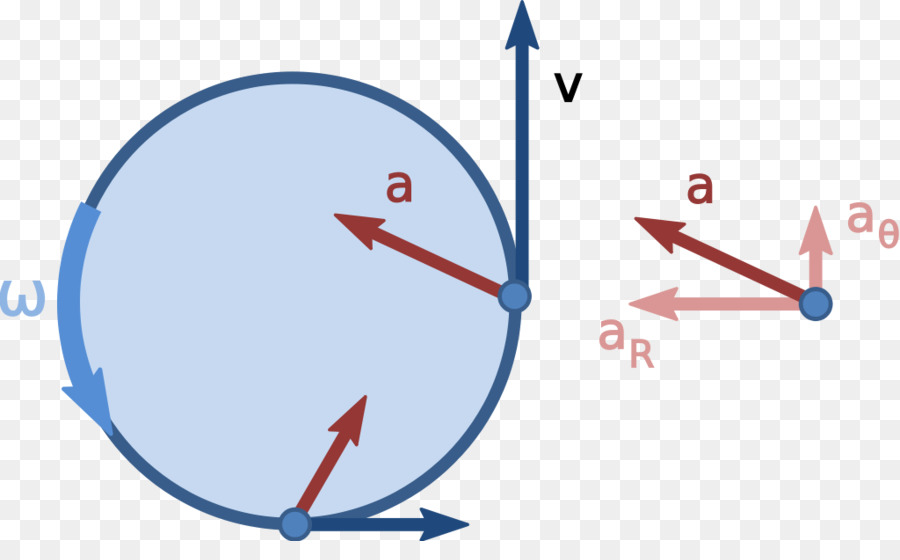
Для решения задачи воспользуемся формулой связи между тангенциальным и угловым ускорениями. Получаем:

a_t = α × r

Поскольку равноускоренное движение длилось в течение времени t = 10 секунд, то приобретенная за это время линейная скорость была равна:

v = a_t × t = α × r × t

Полученную формулу подставляем в соответствующее выражение для нормального ускорения:

a_c = v² / r = α² × t² × r

Остается подставить известные значения в это равенство и записать ответ: a_c = 500 м/с².