Изохорная теплоемкость идеального газа

В термодинамике при изучении переходов из начального в конечное состояние некоторой системы важно знать тепловой эффект процесса. С этим эффектом тесно связано понятие теплоемкости. В данной статье рассмотрим вопрос, что понимают под изохорной теплоемкостью газа.

Идеальный газ

Идеальным называется такой газ, частицы которого считаются материальными точками, то есть не имеют размеров, но обладают массой, и у которого вся внутренняя энергия состоит исключительно из кинетической энергии движения молекул и атомов.

Любой реальный газ в идеале никогда не будет удовлетворять описанной модели, поскольку его частицы все же имеют некоторые линейные размеры и взаимодействуют между собой с помощью слабых ван-дер-ваальсовых связей или химических связей другого типа. Однако при низких давлениях и высоких температурах расстояния между молекулами велики, а их кинетическая энергия превышает потенциальную в десятки раз. Все это позволяет применять с высокой степенью точности идеальную модель для реальных газов.

Внутренняя энергия газа

Внутренняя энергия любой системы - это физическая характеристика, которая равна сумме потенциальной и кинетической энергии. Поскольку в идеальных газах можно пренебречь потенциальной энергией, то для них можно записать равенство:

U = E_k.

Где E_k - энергия кинетическая системы. Используя молекулярно-кинетическую теорию и применяя универсальное уравнение состояния Клапейрона-Менделеева, несложно получить выражение для U. Оно записано ниже:

U = z/2*n*R*T.

Здесь T, R и n - абсолютная температура, газовая постоянная и количество вещества соответственно. Величина z - это целое число, показывающее количество степеней свободы, которыми обладает молекула газа.

Изобарная и изохорная теплоемкость

В физике теплоемкостью называется количество теплоты, которое необходимо предоставить изучаемой системе, чтобы нагреть ее на один кельвин. Справедливо также и обратное определение, то есть теплоемкость - это количество теплоты, которое система выделяет при охлаждении на один кельвин.

Проще всего для системы определить изохорную теплоемкость. Под ней понимают теплоемкость при постоянном объеме. Поскольку система в таких условиях работу не совершает, то вся энергия расходуется на повышение внутренних энергетических запасов. Обозначим изохорную теплоемкость символом C_V, тогда можно записать:

dU = C_V*dT.

То есть изменение внутренней энергии системы прямо пропорционально изменению ее температуры. Если сравнить это выражение, с записанным в предыдущем пункте равенством, то приходим к формуле для C_V в идеальном газе:

С_V = z/2*n*R.

Данной величиной на практике неудобно пользоваться, поскольку она зависит от количества вещества в системе. Поэтому было введено понятие удельной изохорной теплоемкости, то есть величины, которую рассчитывают либо на 1 моль газа, либо на 1 кг. Обозначим первую величину символом C_Vⁿ, вторую - символом C_V^m. Для них можно записать такие формулы:

C_Vⁿ = z/2*R;

C_V^m = z/2*R/M.

Здесь M - молярная масса.

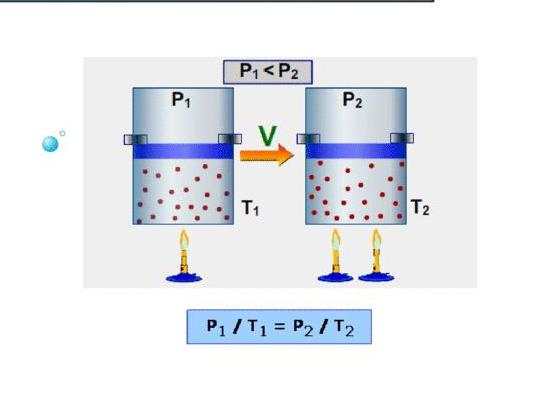
Изобарной называется теплоемкость при поддержании постоянного давления в системе. Примером такого процесса является расширение газа в цилиндре под поршнем при его нагревании. В отличие от изохорного, во время изобарного процесса подводимое к системе тепло расходуется на повышение внутренней энергии и на выполнение механической работы, то есть:

H = dU + P*dV.

Энтальпия изобарного процесса представляет собой произведение изобарной теплоемкости на изменение температуры в системе, то есть:

H = C_P*dT.

Если рассмотреть расширение при постоянном давлении 1 моль газа, то первое начало термодинамики запишется в виде:

C_Pⁿ*dT = C_Vⁿ*dT + R*dT.

Последнее слагаемое получено из уравнения Клапейрона-Менделеева. Из этого равенства следует связь между изобарной и изохорной теплоемкостями:

C_Pⁿ = C_Vⁿ + R.

Для идеального газа удельная молярная теплоемкость при постоянном давлении всегда больше соответствующей изохорной характеристики на величину R=8,314 Дж/(моль*К).

Степени свободы молекул и теплоемкость

Выпишем еще раз формулу для удельной молярной изохорной теплоемкости:

C_Vⁿ = z/2*R.

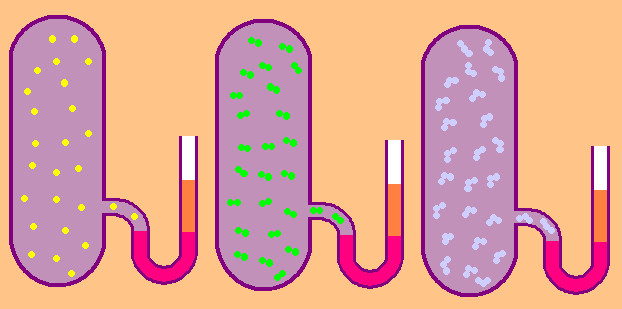
В случае газа одноатомного величина z = 3, поскольку атомы в пространстве могут перемещаться лишь в трех независимых направлениях.

Если же речь идет о газе, состоящем из двухатомных молекул, например, кислород O₂ или водород H₂, то, помимо поступательного движения, эти молекулы могут еще вращаться вокруг двух взаимно перпендикулярных осей, то есть z будет равно 5.

В случае более сложных молекул для определения C_Vⁿ следует использовать z=6.