Когда в школах изучают стереометрию, то большое внимание в учебном процессе обращают на изучение формул и методов расчета объема фигур в пространстве. В данной статье рассмотри что такое призма, и приведем формулы для вычисления объема прямой призмы.
Призма в стереометрии
Прежде чем рассматривать формулы определения объема призмы прямой, разберем подробнее о каком классе геометрическим объектов пойдет речь. Призма - яркий представитель совершенных многогранников, в которых число сторон, вершин и ребер связано равенством Эйлера.
В стереометрии дают следующее простое определение призме: это такой многогранник, в котором две образующие его грани являются абсолютно одинаковыми и находятся в параллельных плоскостях, а остальные грани представляют собой либо параллелограммы, либо прямоугольники (частный случай параллелограмма).
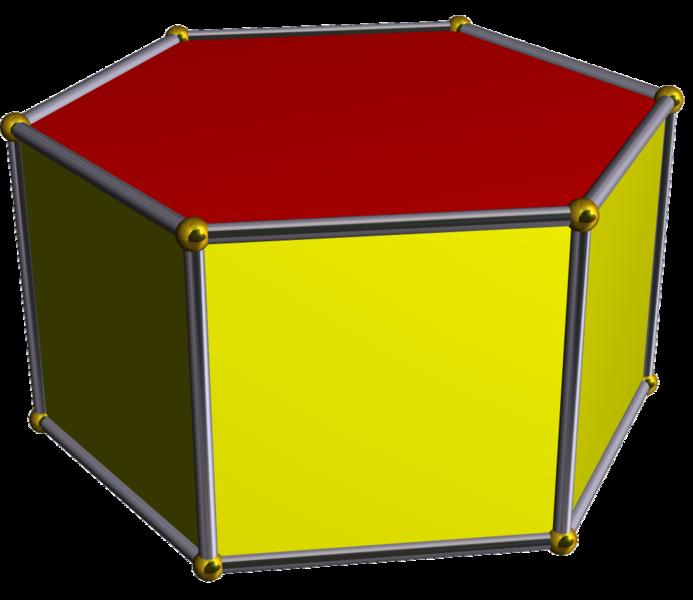
На рисунке показана шестиугольная призма, в которой все названные выше элементы выделены. Так, у нее 12 вершин, 18 ребер и 8 сторон или граней. Желтые стороны в совокупности образуют боковую поверхность, а красная грань - это основание фигуры.
Геометрически любая призма может быть получена с помощью следующей несложной методики. Необходимо взять произвольный многоугольник. Единственное условие заключается в том, что многоугольник должен быть плоским. Затем, с помощью определенного отрезка, который плоскости многоугольника не принадлежит, перенести все его вершины в новую параллельную плоскость. В итоге мы получим каркас призмы.
Виды фигуры и прямая призма
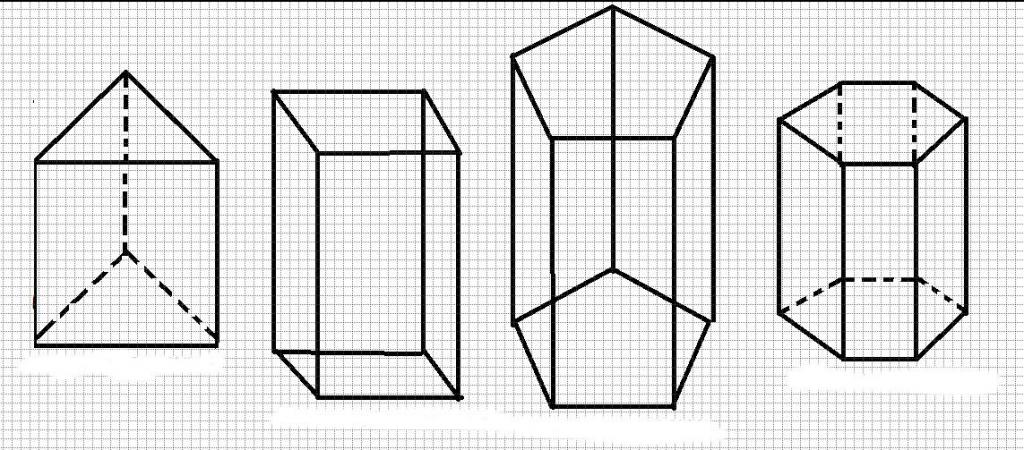
В стереометрии выделяют несколько типов классификаций призм. Фигуры этого класса различают по количеству сторон в основании, по вогнутости или выпуклости основания, по типу всех граней боковой поверхности и по правильной форме основания. Здесь мы не ставим задачей рассмотреть все варианты классификации, а сосредоточим свое внимание только на прямых и наклонных призмах.
Прямая или прямоугольная призма - это такой многогранник, у которого все боковые стороны являются прямоугольниками или квадратами. Другое равноправное с предыдущим определение призмы гласит: если все боковые ребра перпендикулярны основаниям, то имеет место прямоугольная фигура. Обоими определениями можно пользоваться при решении практических задач, поскольку они являются достаточными и необходимыми.
Если в прямой призме основания представляют собой равноугольные и равносторонние многоугольники, то о такой фигуре говорят, что она правильная. Из данных определений понятно, что любая правильная призма будет прямоугольной, но не всякая прямая фигура является правильной.
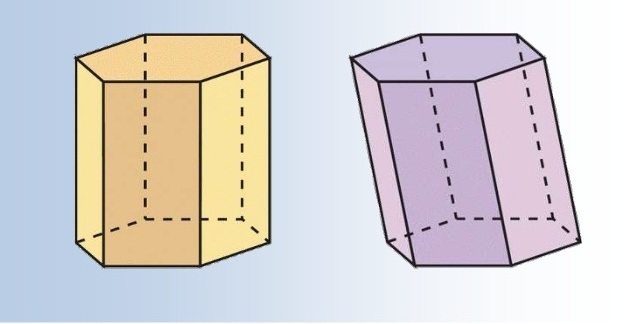
Формула объема прямой призмы
В рассматриваемом виде призмы длина любого ребра бокового равна высоте h фигуры. В то же время как для прямоугольной, так и для наклонной призмы объем определяют по следующей формуле:
V = So × h.
Где символом So обозначена площадь одного основания. Если буквой b обозначить длину ребра бокового, тогда это выражение для прямой фигуры можно переписать в виде:
V = So × b.
Как следует из этих равенств, весь вопрос определения величины V заключается в вычислении площади So. Естественно, что не существует какой-либо определенной формулы для ее определения, поскольку в основании может находиться многоугольник совершенно произвольного типа. Тем не менее для некоторых фигур конкретные формулы записать можно.
Например, если прямая призма является правильной, тогда для So справедлива формула:
So = n / 4 × ctg(pi / n) × a2.
Где n и a - число сторон и длина одной стороны, соответственно.
Другой пример, когда можно привести конкретную формулу, это треугольное основание. Если известны длина стороны a и высота треугольника, опущенная на нее, ha, тогда площадь So рассчитывается так:
So = 1 / 2 × a × ha.
Обратим внимание, что при использовании формулы для V фигуры, следует в нее подставлять площадь одного, а не двух оснований.
Пример решения задачи
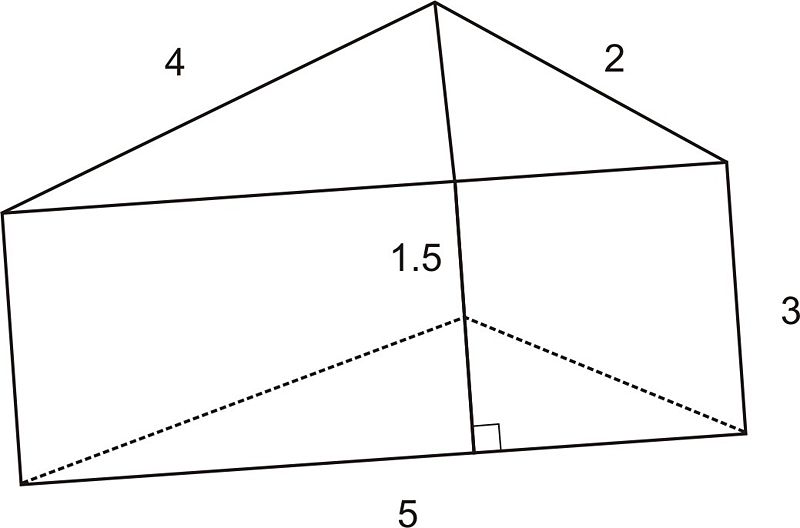
Необходимо определить объем призмы прямой, основанием которой является прямоугольный треугольник. Гипотенуза треугольника равна 12 см, а один из его катетов составляет 4 см. Высота объемной фигуры равна 10 см.
Из курса планиметрии каждый школьник знает, что половина произведения катетов дают площадь соответствующего треугольника. Пользуясь теоремой Пифагора, получаем второй катет:
a2 = √(c2 – a12) = √(122 – 42) = 11,31 см.
Тогда площадь So треугольника составит:
So = 4 × 11,31 / 2 = 22,62 см2.
Применяя формулу для объема, получаем:
V = 22,62 × 10 = 226,2 см3.
Таким образом, объем прямой призмы равен 226,2 см3.


























