Прямоугольная призма. Формулы длин диагоналей, площади поверхности и объема

Стереометрия является разделом геометрии, который изучает разные свойства фигур в пространстве трехмерной системы координат. Одной из таких фигур является прямоугольная призма. Что она собой представляет, и какие свойства для нее характерны, рассмотрим в данной статье.

Призма прямоугольная в стереометрии

Каждый человек знаком с этой совершенной геометрической фигурой. Под ней понимают объемный объект, который состоит из шести прямоугольников в общем случае, причем все они попарно равны. Получить в пространстве эту призму несложно. Необходимо взять произвольный прямоугольник и перенести его параллельно самому себе вдоль отрезка, перпендикулярного исходному прямоугольнику. В результате получится фигура, показанная ниже на рисунке.

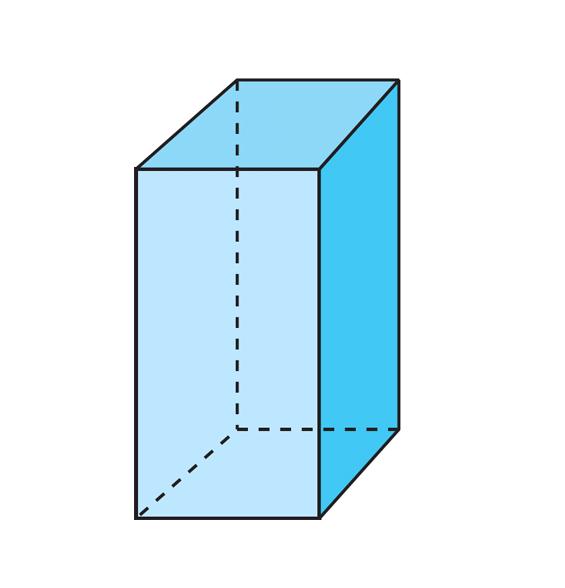
Прямоугольная призма также называется параллелепипедом. Если ее основание будет квадратом, то она станет правильной призмой, у которой боковые прямоугольники будут равны между собой. Если у правильной призмы сторона основания совпадет с высотой (длиной ребра бокового), тогда мы получим фигуру куб.

Элементы фигуры

Речь идет о геометрических элементах, из которых состоит рассматриваемая призма. Первое, что бросается в глаза при первом взгляде на фигуру - это ее грани. Как было отмечено, у нее их шесть. Две одинаковые грани образуют основания прямоугольной призмы, четыре оставшиеся составляют ее боковую поверхность. Все грани являются или прямоугольниками, либо квадратами.

Следующий важный элемент фигуры - это ребра. Призма имеет 12 ребер, причем 8 из них принадлежат основаниям. Оставшиеся четыре ребра являются боковыми. Их длина равна высоте фигуры.

Наконец, третьим важным элементом изучаемой призмы являются ее вершины. В отличие от пирамиды или конуса, призма не имеет выделенной вершины. Все они у нее являются равноправными. Их количество равно восьми.

Как видно из представленной количественной характеристики элементов прямой прямоугольной призмы, для их чисел справедлива теорема Эйлера:

число ребер = число сторон + число вершин - 2 =>

12 = 6 + 8 - 2.

Диагонали фигуры

Диагонали прямоугольной призмы бывают двух видов:

• те, которые расположены в плоскости граней фигуры;
• те, что находятся в объеме.

Если обозначить буквами a, b и h длины сторон основания и длину бокового ребра, соответственно, тогда для длины диагоналей первого типа можно записать следующие равенства:

d₁ = √(a² + b²);

d₂ = √(a² + h²);

d₃ = √(h² + b²).

Диагональ d₁ принадлежит основаниям, а диагонали d₂ и d₃ лежат в плоскостях боковых прямоугольников. Очевидно, что записанные формулы следуют из теоремы Пифагора.

Что касается диагоналей второго типа (объемных), то любая прямоугольная призма имеет четыре таких диагонали. Тем не менее их длины равны между собой. Формула для определения длины объемной диагонали записывается в следующем виде:

d₄ = √(a² + b² + h²).

Если вычислять диагональ d₄ для куба, то можно записать следующее выражение, которое получается из предыдущего:

d₄ = a*√3.

При этом, все диагонали граней куба будут равны друг другу, и их длины вычисляются так:

d₁ = d₂ = d₃ = a*√2.

Длина объемной диагонали всегда больше длин диагоналей сторон.

Определение площади поверхности

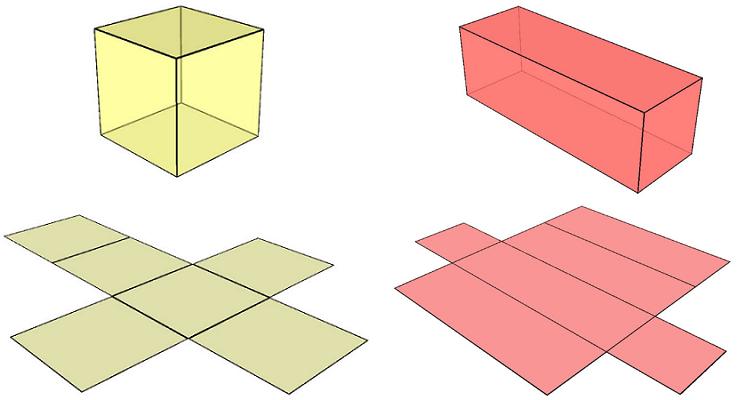
Каждый школьник знает, что для удобного определения площади поверхности, которой обладает любая объемная фигура, следует сделать ее развертку на плоскости. Прямоугольная призма не является исключением. Ее развертку сделать просто, для этого следует отрезать два основания от фигуры, а затем, разрезать ее вдоль одного из боковых ребер. Развернув грани боковой поверхности, мы получим следующую картину.

Развертка представляет собой шесть прямоугольников трех видов. Обозначим стороны основания буквами a и b. Высоту фигуры обозначим h. Тогда площадь одного основания будет равна:

S_o = a*b

Площади двух разных боковых граней равны:

S₁ = a*h;

S₂ = b*h.

Поскольку параллелепипед имеет по паре одинаковых граней, формулы площадей для которых записаны, то площадь полной поверхности фигуры S будет равна:

S = 2*(S_o + S₁ + S₂) = 2*(a*b + a*h + b*h).

Формула для S может быть упрощена, если прямоугольная призма обладает дополнительной симметрией. Например, если стороны ее основания равны (a = b), тогда для S можно записать такое выражение:

S = 2*a*(a + 2*h).

Это выражение следует из предыдущей формулы. Соответственно, если высота и длина основания равны (h=a), то мы получаем куб, площадь поверхности которого составит:

S = 6*a².

Заметим чем выше симметрия параллелепипеда, тем меньшее число линейных параметров необходимо знать, чтобы вычислить величину S.

Объем призмы прямоугольной

Изучаемая фигура состоит из шести граней, которые ограничивают пространственный объем. Он является объемом самой фигуры. Чтобы его рассчитать, можно применить универсальную формулу для всех призм и цилиндров. Она имеет следующий вид:

V = S_o*h

Поскольку основание изучаемой фигуры является прямоугольником, а ее высота равна длине ребра бокового, то объем призмы прямоугольной будет равен:

V = a*b*h

Полезно также привести формулы для правильной призмы с квадратным основанием и для куба, их объемы рассчитываются следующим образом:

для правильной призмы: V = a²*h;

для куба: V = a³.

Как и для площади, для определения объема необходимо знать от 1 до 3 линейных параметров в зависимости от симметрии параллелепипеда.