Физика твердого тела изучает множество различных видов движения. Основные из них - это поступательное движение и вращение по неподвижной оси. Также существуют и их комбинации: свободное, плоское, криволинейное, равноускоренное и другие разновидности. Каждое движение имеет свои особенности, но и сходство между ними, конечно, есть. Рассмотрим, какое движение называется вращательным и приведем примеры такого движения, проведя аналогию с движением поступательным.
Законы механики в действии
На первый взгляд кажется, что вращательное движение, примеры которого мы наблюдаем в повседневной деятельности, нарушает законы механики. В чем можно заподозрить это нарушение и каких законов?
Например, закон инерции. Всякое тело, когда на него не действуют неуравновешенные силы, должно или находиться в состоянии покоя, или совершать равномерное прямолинейное движение. Но если дать глобусу боковой толчок, он начнет вращаться. И он, скорее всего, вращался бы вечно, если бы не трение. Как и отличный пример вращательного движения – земной шар – вращается постоянно, никем не подталкиваемый. Получается, что первый закон Ньютона в этом случае не действует? Это не так.
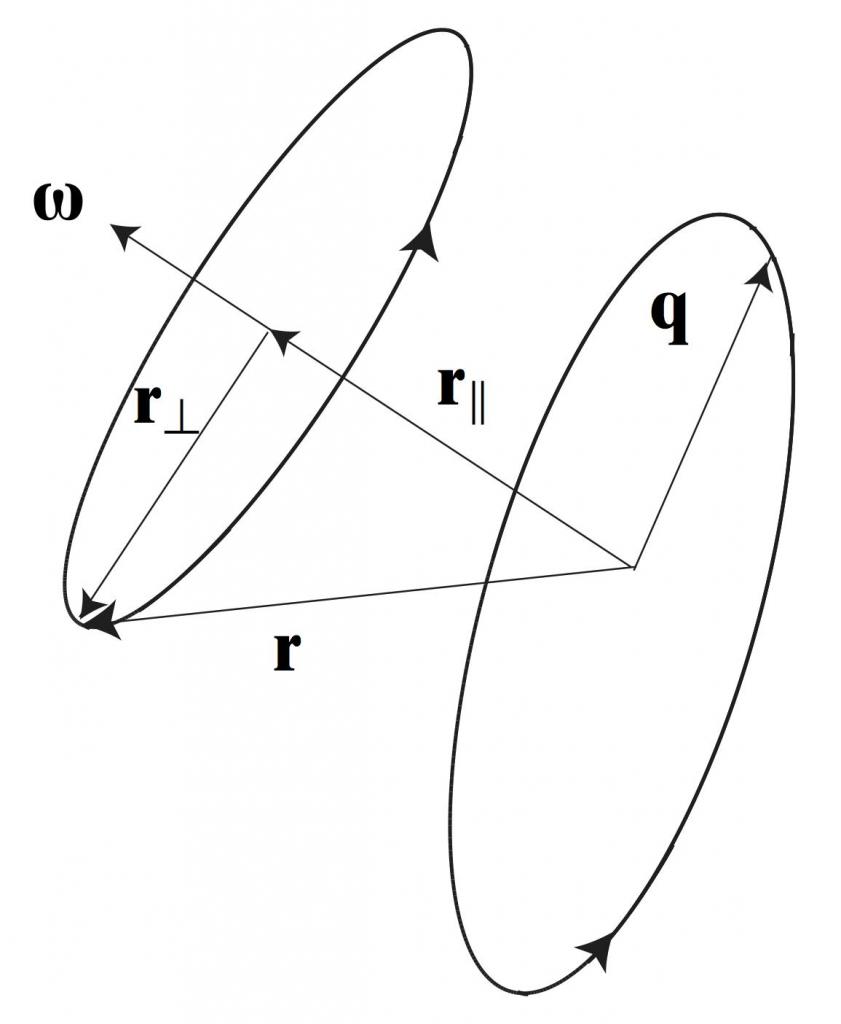
Что движется: точка или тело
Вращательное движение отличается от поступательного, но между ними есть и много общего. Стоит сопоставить и сравнить эти виды, рассмотреть примеры поступательного и вращательного движения. Для начала следует строго разграничить механику материального тела и механику материальной точки. Вспомним определение поступательного движения. Это такое движение тела, при котором каждая его точка движется одинаково. Это означает, что все точки физического тела в каждый конкретный момент времени имеют одинаковую по модулю и направлению скорость и описывают одинаковые траектории. Поэтому, поступательное движение тела можно рассматривать как движение одной точки, а точнее, движение его центра масс. Если на такое тело (материальную точку) не будут действовать другие тела, то оно находится в покое, или движется прямолинейно и равномерно.

Сравнение формул для вычисления
Примеры вращательного движения тел (глобус, колесо) показывают, что вращение тела характеризуется угловой скоростью. Она обозначает, на какой угол оно повернется за единицу времени. В технике угловую скорость часто выражают числом оборотов в минуту. Если угловая скорость постоянна, то можно говорить, что тело вращается равномерно. Когда угловая скорость равномерно возрастает, то вращение называется равноускоренным. Сходство законов поступательного и вращательного движений очень значительно. Отличаются только буквенные обозначения, а формулы вычисления – одинаковы. Это хорошо видно в таблице.
| Поступательное движение | Вращательное движение | |
| Скорость v Путь s Время t Ускорение a | Угловая скорость ω Угловое перемещение φ Время t Угловое ускорение ą | |
| s = v * t | φ = ω * t | |
| v = a * t S = a*t2 / 2 | ω = ą * t φ = ą*t2 / 2 |
Все задачи по кинематике как поступательного, так и вращательного движения аналогично решаются по этим формулам.
Роль силы сцепления
Рассмотрим примеры вращательного движения в физике. Возьмем движение одной материальной точки – тяжелого металлического шарика от шарикоподшипника. Можно ли сделать так, чтобы он двигался по окружности? Если толкнуть шарик, то он покатится по прямой. Можно вести шарик по окружности, все время его поддерживая. Но стоит только убрать руку, и он продолжит движение по прямой линии. Из этого следует вывод, что точка может двигаться по окружности только под действием силы.

Это движение материальной точки, но в твердом теле не одна точка, а множество. Они связаны между собой, так как на них действуют силы сцепления. Именно эти силы и удерживают точки на круговой орбите. При отсутствии силы сцепления материальные точки вращающегося тела разлетелись бы, как грязь слетает с вращающегося колеса.
Линейная и угловая скорости
Эти примеры вращательного движения позволяют провести еще одну параллель между вращательным и поступательным движением. Во время поступательного движения все точки тела двигаются в определенный момент времени с одинаковой линейной скоростью. При вращении тела все его точки двигаются с одинаковой угловой скоростью. При вращательном движении, примеры которого – спицы вращающегося колеса, угловые скорости всех точек вращающейся спицы будут одинаковы, а линейные – различны.
Ускорение – не в счет
Вспомним, что в равномерном движении точки по окружности всегда присутствует ускорение. Такое ускорение называется центростремительным. Оно показывает только изменение направления скорости, но не характеризует изменение скорости по модулю. Поэтому можно говорить о равномерном вращательном движении с одной угловой скоростью. В технике, при равномерном вращении маховика или ротора электрического генератора, угловую скорость считают постоянной. Только постоянное количество оборотов генератора может обеспечить постоянное напряжение в сети. А такое число оборотов маховика гарантирует плавный и экономичный ход машины. Тогда вращательное движение, примеры которого приведены выше, характеризуется только угловой скоростью, без учета центростремительного ускорения.

Сила и ее момент
Есть еще одна параллель между поступательным и вращательным движением – динамическая. Как гласит второй закон Ньютона, ускорение, получаемое телом, определяется как деление приложенной силы на массу тела. При вращении изменение угловой скорости зависит от силы. Ведь при завинчивании гайки определяющую роль играет вращающее действие силы, а не то, куда эта сила приложена: к самой гайке или к рукоятке гаечного ключа. Таким образом, показателю силы в формуле поступательного движения при вращении тела соответствует показатель момента силы. Наглядно это можно отобразить в виде таблицы.
| Поступательное движение | Вращательное движение |
| Сила F | Момент силы M=Fl, где l - плечо силы |
| Работа A = F * s | Работа A = M * φ |
| Мощность N=Fs/t=Fv | Мощность N=Mφ/t=Mω |
Масса тела, его форма и момент инерции
В приведенной таблице не проводится сравнение по формуле второго закона Ньютона, так как это требует дополнительного объяснения. В эту формулу входит показатель массы, который характеризует степень инертности тела. При вращении тела его инертность не характеризуется его массой, а определяется такой величиной, как момент инерции. Этот показатель находится в прямой зависимости не столько от массы тела, сколько от его формы. То есть имеет значение то, как в пространстве масса тела распределена. Тела различной формы будут иметь разные значения момента инерции.
При вращении материального тела по окружности его момент инерции будет равен произведению массы вращающегося тела на квадрат радиуса оси вращения. Если точка переместится от оси вращения на вдвое большее расстояние, то показатель момента инерции и устойчивость вращения увеличатся в четыре раза. Вот почему маховые колоса делают большими. Но и слишком сильно увеличивать радиус колеса нельзя, так как при этом растет центростремительное ускорение точек его обода. Образующая это ускорение сила сцепления молекул может стать недостаточной для удержания их на круговом пути, и колесо разрушится.

Итоговое сравнение
При проведении параллели между вращательным и поступательным движением, следует понять, что при вращении роль массы тела играет момент инерции. Тогда динамический закон вращательного движения, соответствующий второму закону Ньютона, будет гласить, что момент силы равен произведению момента инерции и углового ускорения.
Теперь можно провести сравнение всех формул основного уравнения динамики, импульса и кинетической энергии при поступательном и вращательном движении, примеры расчета которых уже известны.
| Поступательное движение | Вращательное движение |
| Основное уравнение динамики F = m * a | Основное уравнение динамики M = I * ą |
| Импульс p = m * v | Импульс p = I * ω |
| Кинетическая энергия Ek = mv2 / 2 | Кинетическая энергия Ek = Iω2 / 2 |
Поступательное и вращательное движения имеют много общего. Нужно только разобраться, как в каждом из этих видов ведут себя физические величины. При решении задач используются очень похожие формулы, сравнение которых приведено выше.



























