Оптимизация помогает найти наилучший результат, который приносит прибыль, уменьшает затраты или устанавливает параметр, вызывающий сбои бизнес-процессов.
Этот процесс также называют математическим программированием. Оно решает проблему определения распределения ограниченных ресурсов, необходимых для достижения поставленной цели руководителем оптимизационной задачи. Из всех допустимых вариантов желательно найти тот, который максимально усиливает (или уменьшает) контролирующий параметр, например, прибыль или стоимость. Модели оптимизации также называются предписывающими или нормативными, поскольку стремятся найти возможную стратегию для бизнеса.
История развития
Линейное программирование (ЛП) работает с классом задач оптимизации, где все ограничения являются линейными.

Представляет краткую историю развития ЛП:
- В 1762 году Лагранж решил простые оптимизационные задачи с ограничениями равенства.
- В 1820-м Гаусс решил линейную систему уравнений с помощью исключения.
- В 1866- м Вильгельм Джордан усовершенствовал метод поиска ошибок наименьших квадратов, как критерий соответствия. Теперь это называется методом Гаусса-Джордана.
- В 1945-м появился цифровой компьютер.
- В 1947-м Данциг изобрел симплексные методы.
- В 1968-м Фиакко и Маккормик представили метод «Внутренняя точка».
- В 1984 году Кармаркар применил метод интерьера для решения линейных программ, добавив свой инновационный анализ.
ЛП оказалось чрезвычайно мощным инструментом как для моделирования реальных задач, так и в качестве широко применяемой математической теории. Однако многие интересные оптимизационные задачи являются нелинейными.
Что делать в этом случае? Исследование таких проблем включает в себя разнообразную смесь линейной алгебры, многомерного исчисления, численного анализа и вычислительных методов. Ученые занимаются разработкой вычислительных алгоритмов, включая методы внутренних точек для линейного программирования, геометрию, анализ выпуклых множеств и функций, а также изучение специально структурированных задач, таких как квадратичное программирование.
Нелинейная оптимизация обеспечивает фундаментальное понимание математического анализа и широко используется в различных областях, таких как проектирование, регрессионный анализ, управление запасами, геофизических исследований и экономике.
Классификация оптимизационных задач
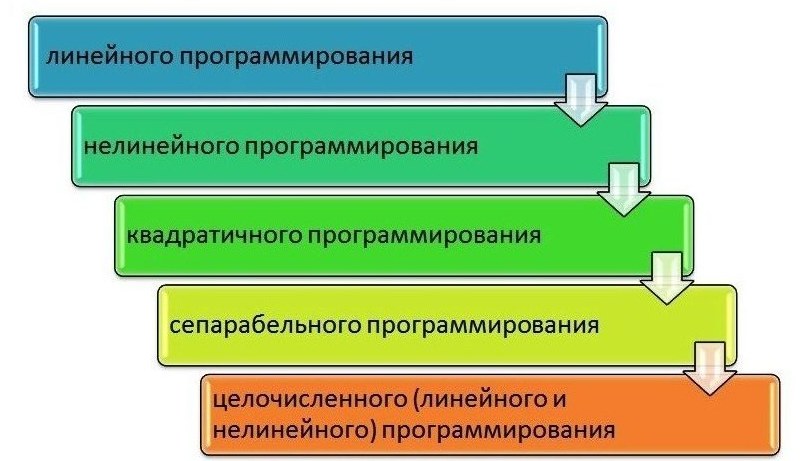
Важным шагом в процессе оптимизации является классификация моделей, поскольку их алгоритмы решения адаптированы к конкретному типу.
1. Задачи с дискретной и непрерывной оптимизацией. Одни модели имеют смысл только в том случае, если переменные принимают значения из дискретного набора подмножества целых чисел. Другие содержат данные, которые могут принимать любое реальное значение. Их, как правило, легче решать. Усовершенствования алгоритмов в сочетании с достижениями в области вычислительной техники резко увеличили размер и сложность оптимизационной задачи линейного программирования.
2. Неограниченная и ограниченная оптимизация. Еще одно важное различие - это задачи, в которых нет ограничения на переменные. Оно может широко варьироваться от простых оценок до систем равенств и неравенств, которые моделируют сложные отношения между данными. Такие задачи оптимизации могут быть дополнительно классифицированы по характеру функций (линейные и нелинейные, выпуклые и гладкие, дифференцируемые и недифференцируемые).
3. Задачи выполнимости. Их цель состоит в том, чтобы найти значения переменных, которые удовлетворяют ограничениям модели без какой-либо конкретной цели оптимизации.
4. Задачи комплементарности. Они широко распространены в технике и экономике. Цель состоит в том, чтобы найти решение, которое удовлетворяет условиям дополнительности. На практике задачи с несколькими целями часто переформулируются в единые объективные.
5. Детерминированная против стохастической оптимизации. При детерминированной оптимизации предполагается, что данные для задачи абсолютно точные. Однако по многим актуальным вопросам они не могут быть известны по ряду причин.
Первая связана с простой ошибкой измерения. Вторая причина более фундаментальная. Она заключается в том, что некоторые данные представляют информацию о будущем, например, спрос на продукт или цену на будущий период времени. При оптимизации в условиях стохастической оптимизации неопределенность включается в модель.
Основные компоненты
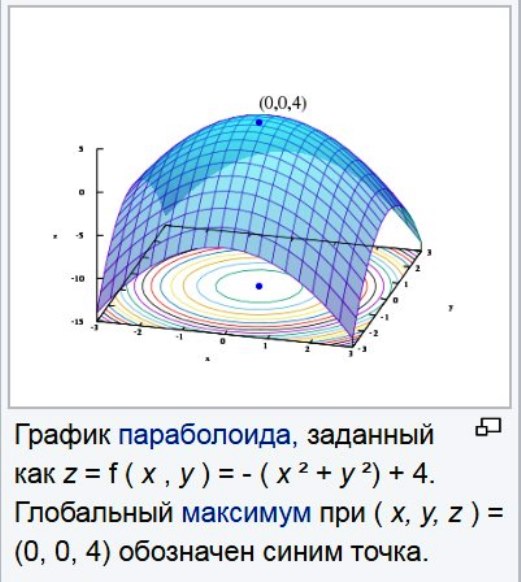
Целевая функция - это та, которую нужно минимизировать или максимизировать. Большинство видов оптимизационных задач имеют одну целевую функцию. Если нет, то их часто можно переформулировать так, чтобы они выполнялись.
Два исключения из этого правила:
1. Задача поиска цели. В большинстве бизнес-приложений менеджер желает достичь конкретной цели, одновременно удовлетворяя ограничения модели. Пользователь не особенно хочет что-то оптимизировать, поэтому нет смысла определять целевую функцию. Этот тип обычно называют проблемой выполнимости.
2. Множество объективных функций. Зачастую пользователь хотел бы оптимизировать сразу несколько разных целей. Обычно они несовместимы. Переменные, которые оптимизируют одну цель, могут быть далеко не лучшими для других.
Типы компонентов:
- Управляемые входные данные - это набор переменных решения, которые влияют на значение целевой функции. В производственной задаче переменные могут включать в себя распределение различных доступных ресурсов или трудозатраты, необходимые для каждого действия.
- Ограничения - это отношения между переменными решениями и параметрами. Для производственной проблемы не имеет смысла тратить большое количество времени на какую-либо деятельность, поэтому ограничивают все «временные» переменные.
- Возможные и оптимальные решения. Значение решения для переменных, при котором все ограничения выполняются, называется выполнимым. Большинство алгоритмов вначале его находят, затем пытаются улучшить. Наконец, они изменяют переменные, чтобы перейти от одного выполнимого решения к другому. Данный процесс повторяется до тех пор, пока целевая функция не достигнет своего максимума или минимума. Этот результат называется оптимальным решением.
Широко используются алгоритмы оптимизационных задач, разработанные для следующих математических программ:
- Выпуклые.
- Разделяемые.
- Квадратичные.
- Геометрические.
Линейные решатели Google

Линейная оптимизация или программирование - это имя, которое дается вычислительному процессу оптимального решения задачи. Она моделируется в качестве набора линейных отношений, которые возникают во многих научных и инженерных дисциплинах.
Google предлагает три способа решения задач линейной оптимизации:
- Библиотека с открытым исходным кодом Glop.
- Надстройка Linear Optimization для Google Sheets.
- Служба линейной оптимизации в Google Apps Script.
Glop - это встроенный в Google линейный решатель. Он доступен с открытым исходным кодом. Можно получить доступ к Glop через упаковщик линейного решателя OR-Tools, который является оболочкой для Glop.
Модуль линейной оптимизации для Google Sheets позволяет выполнять линейную постановку оптимизационной задачи, вводя данные в электронную таблицу.
Квадратичное программирование
Платформа Premium Solver использует расширенную LP/Quadratic версию метода Simplex с ограничениями обработки задач LP и QP до 2000 переменных решений.
SQP Solver для крупномасштабных задач использует современную реализацию метода активного набора с разреженностью для решения задач квадратичного программирования (QP). Механизм XPRESS Solver использует естественное расширение метода "Внутренней точки" или Ньютона-Барьера для решения проблем QP.
MOSEK Solver применяет методы внедренной "Внутренней точки" и автодуальный. Это особенно эффективно для слабосвязанных задач QP. Он также может решать задачи масштабного квадратичного ограничения (QCP) и конусного программирования второго порядка (SOCP).
Многооперационные вычисления
Они вполне успешно используются с применением возможностей Microsoft Office, например, решение оптимизационных задач в Excel.
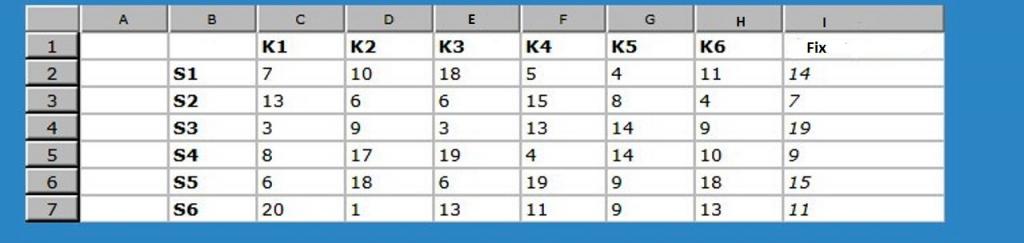
В приведенной выше таблице такие обозначения:
- K1 - K6 - клиенты, которым необходимо предоставить товар.
- S1 - S6 - потенциальные производственные площадки, которые могут быть построены для этого. Может быть создано 1,2,3,4,5 или все 6 локаций.
Для каждого объекта есть фиксированные затраты, указанные в столбце I (Fix).
Если местоположение ничего не меняет, оно не будет учитываться. Тогда не будет фиксированных затрат.
Определяют потенциальные местоположения, чтобы получить самую низкую стоимость.
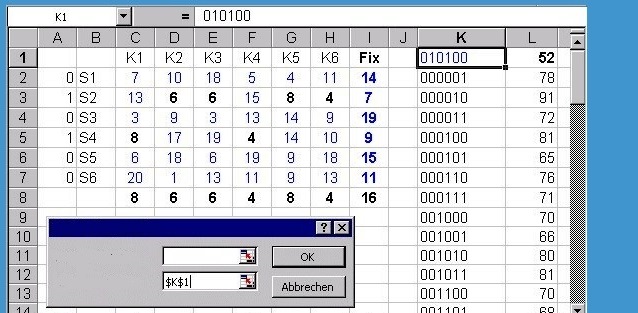
В данных условиях местоположение либо установлено, либо нет. Это два состояния таковы: «ИСТИНА – ЛОЖЬ» или «1 – 0». Существует шесть состояний для шести местоположений, например, для 000001 установлено только шестое , для 111111 - все.
В двоичной системе счисления существует ровно 63 различных варианта от 000001 (1) до 111111 (63).
В L2-L64 теперь должно стоять {= MULTIPLE OPERATION (K1)}, это результаты всех альтернативных решений. Тогда минимальное значение равно = Min (L), а соответствующая альтернатива равна INDEX (K).
Целочисленное программирование CPLEX
Иногда линейных отношений недостаточно, чтобы уловить суть бизнес-проблемы. Это особенно верно, когда решения включают дискретный выбор, например, открывать склад в определенном месте или нет. В этих ситуациях необходимо использовать целочисленное программирование.
Если проблема включает в себя как дискретный, так и непрерывный выбор, это смешанная целочисленная программа. Она может иметь линейные, выпуклые квадратичные задачи и такие же ограничения второго порядка.
Целочисленные программы гораздо сложнее, чем линейные, но они имеют важные бизнес-приложения. Программное обеспечение CPLEX использует сложные математические методы для решения целочисленных задач. Его методы включают в себя систематический поиск возможных комбинаций дискретных переменных с использованием линейных или квадратичных программных релаксаций для вычисления границ значения оптимального решения.
Они также используют LP и другие методы решения оптимизационных задач для вычисления ограничений.
Стандартный Microsoft Excel Solver
Эта технология использует базовую реализацию основного метода Simplex для решения задач LP. Он ограничен 200 переменными. "Премиум Солвер" использует улучшенный первичный симплекс-метод с двухсторонними границами для переменных. Платформа Premium Solver использует расширенную версию LP/Quadratic Simplex Solver для решения оптимизационной задачи с числом переменных решений до 2000.
Крупномасштабная LP для платформы Premium Solver применяет современную реализацию метода простого и двойного симплекса, который использует разреженность в модели LP для экономии времени и памяти, передовые стратегии для обновления и рефакторизации матриц, многократного и частичного ценообразования и поворотов, а также для преодоления вырождения. Этот механизм доступен в трех версиях (с возможностью обработки до 8 000, 32 000 или неограниченного числа переменных и ограничений).
MOSEK Solver включает в себя первичный и двойственный симплекс - метод, который также эксплуатирует разреженность и использует передовые стратегии для обновления матрицы и «refactorization». Он решает задачи неограниченного размера, был протестирован на задачах линейного программирования с миллионами переменных решений.
Пошаговый пример в EXCEL
Чтобы определить модель оптимизационной задачи в Excel, выполняют следующие этапы:
- Организовывают данные для проблемы в электронной таблице в логической форме.
- Выбирают ячейку для хранения каждой переменной.
- Создают в ячейке формулу вычисления целевой математической модели оптимизационной задачи.
- Создают формулы для расчета левой части каждого ограничения.
- Используют диалоги в Excel, чтобы сообщить "Солверу" о переменных решения, целях, ограничениях и желаемых границах этих параметров.
- Запускают "Солвер", чтобы найти оптимальное решение.
- Создают лист Excel.
- Упорядочивают данные для проблемы в Excel, где рассчитывается формула для целевой функции и ограничения.
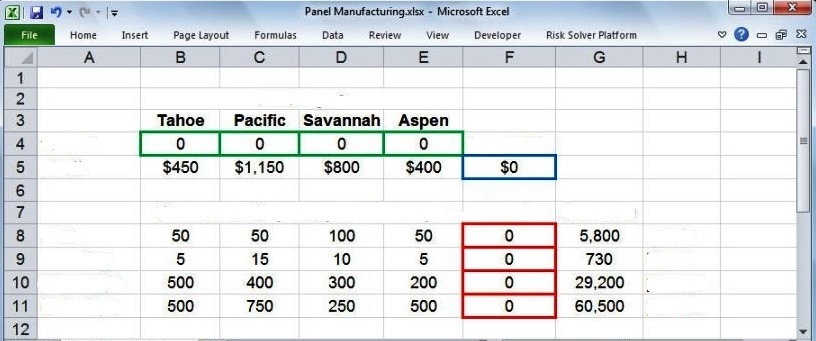
В приведенной выше таблице зарезервировали ячейки B4, C4, D4 и E4 для представления переменных принятия решения X 1, X 2, X 3 и X 4. Примеры решения:
- Модель ассортимента продукции (прибыль для каждого вида изделий 450, 1150, 800 и 400 долларов) была введена в ячейки B5, C5, D5 и E5 соответственно. Это позволяет вычислить цель в F5 = B5 * B4 + C5 * C4 + D5 * D4 + E5 * E4 или F5: = SUMPRODUCT (B5: E5, B4: E4).
- В B8 вводят количество ресурсов, необходимое для изготовления продукции каждого типа.
- Формула для F8: = SUMPRODUCT (B8: E8, $ B $ 4: $ E $ 4).
- Копируют эту формулу в F9. Знаки доллара в $ B $ 4: $ E $ 4 указывают, что этот диапазон ячеек остается постоянным.
- В G8 вводят доступное количество ресурсов каждого типа, соответствующее значениям ограничений справа. Это позволяет выразить их так: F11<= G8: G11.
- Это эквивалентно четырем ограничениям F8<= G8, F9 <= G9, F10 <= G10 и F11 <= G11. Можно ввести этот набор непосредственно в диалогах Solver вместе с условиями неотрицательности B4: E4> = 0
Области практического применения метода
Линейная оптимизация имеет много практических приложений в качестве примера оптимизационной задачи:
Компания может сделать несколько продуктов с известной маржой вклада. Производство единицы каждого изделия требует известное количество ограниченных ресурсов. Задача - создание производственной программы для определения того, сколько каждого продукта должно быть произведено так, чтобы прибыль компании была максимальной, не нарушая ресурсные ограничения.
Проблемы смешивания - это решение оптимизационных задач, связанных с объединением ингредиентов в конечный продукт. Примером этого является проблема диеты, изученная Джорджем Данцигом в 1947 году. Приведен ряд сырьевых материалов, например, овса, свинины и подсолнечного масла, а также содержание в них питательных веществ, например, белка, жира, витамина А и их цена за килограмм. Задача состоит в том, чтобы смешать один или несколько конечных продуктов из сырья с минимальными затратами при условии соблюдения минимальных и максимальных пределов для их пищевой ценности.
Классическим применением линейной оптимизационной задачи является определение маршрутизации для потребностей трафика в телекоммуникационных или транспортных сетях. При этом потоки должны маршрутизироваться через сеть таким образом, чтобы все требования к трафику выполнялись без нарушения условий пропускной способности.
В рамках математической теории линейная оптимизация может использоваться для вычисления оптимальных стратегий в играх с нулевой суммой для двух человек. При этом рассчитывается распределение вероятностей для каждого участника, что является коэффициентом случайного смешения его стратегий.
Без оптимизации невозможен ни один успешный бизнес-процесс в мире. Существует много доступных алгоритмов оптимизации. Некоторые методы подходят только для определенных типов проблем. Важно уметь распознавать их характеристики и подбирать подходящий метод решения.



























