Автор книги «Как не ошибаться. Сила математического мышления» Джордан Элленберг считает, что каждый может разобраться в существующих арифметических понятиях, и верит, что полученные сведения смогут расширить кругозор любого.
Числовой подход к жизни
В твердом переплете раскрывается логика и нестандартный подход, позволяющие многое объяснить. Преподаватель математики и автор многочисленных публикаций и газетных заметок в «The Washington Post» в «New York Times» представляет читателям школьный предмет не как скучный перечень правил, а как центральную систему, на основе которой держится все. Математика – это шанс увидеть завуалированные микроструктуры мироздания, понять истинное значение исходных данных и критически их осмыслить.

Обыденная жизнь состоит из многочисленных вопросов, которые волнуют каждого жителя планеты. Почему у мужчины и женщины высокого роста рождаются дети, совершенно не похожие на родителей, какое мнение принято считать общественным, кто сможет победить на следующих выборах, каков процент образования раковой опухоли у здорового человека? Элленберг в книге «Как не ошибаться. Сила математического мышления» представляет читателю метод анализа жизненных вопросов, где описаны явления и идеи (рейганомика, лотерейные схемы), которые объясняются в доступной форме. Автор утверждает, что это пособие поможет понять мир глубже. Особенно тем, кто интересуется математикой.
Немного о Джордане
Элленберг в детстве был вундеркиндом, читать научился благодаря телевизионным передачам. В восьмом классе ему предложили посещать занятия в Мэрилендском университете. На данном жизненном этапе автор книги «Как не ошибаться. Сила математического мышления» Джордан Элленберг является учителем этого предмета в вузе Висконсина, и, одновременно, занимается публикацией статей на аналогичные темы. Он, по средствам данного учебника, хочет показать читателю, что наука на ограничивается обычными расчетами, это навык нестандартного мышления, что помогает избегать часто совершаемые ошибки.

История наименования
На вопрос, почему книгу «Как не ошибаться. Сила математического мышления» автор назвал именно так, и какова была задумка, Джордан ответил, что идея зародилась довольно давно, и, изначально, ему хотелось изложить свои мысли о силе точной науки. По его мнению, настроиться на проживание жизненного пути без неверных шагов – чересчур надменно, но составить план, что будет помогать избегать заранее неверных шагов – практично.
Математике подчиняются большая часть жизнедеятельности личности, но, даже гуманитарии, которые не любят алгоритмы и цифры, бывают благоуспешными. Есть разница между «быть неравнодушным» к математике и пониманием ее сущность. Если человек сможет понять математическую идеологию, знания этой науки его обогатят.
Статистика и военные задачи
Книга Джордана Элленберга «Как не ошибаться. Сила математического мышления» рассчитана на каждого, кто хочет изменить свою жизнь, кто хочет взглянуть на все с этой точки зрения. В своем пособии он берет статистические исследования специалистов и на примерах доказывает свои теории.

Одним из наглядных примеров является решение задач военного назначения. На обсуждение был вынесен вопрос о том, сколько брони необходимо добавить истребителям, и какие места следует усилить, чтобы их было сложнее сбить, но, при этом, не пострадала их маневренность. Была составлена таблица, в которой расписали повреждения самолетов.
Абрахам Вальд утверждал, что необходимо уделять внимание лишь защите двигателя, в связи с тем, что самолеты с пробоинами в определенных местах, возвращались на базу, в отличие от тех, что получали пулю в рабочий двигатель. Почему Вальд заметил то, на что не обратили внимание офицеры? Причина, как уверен Элленберг в «Как не ошибаться. Сила математического мышления» - в соответствующем строении мышления Абрахама. Человек, чья жизнь основывается на числах, при решении задач ставит перед собой вопросы: «Из каких предположений исходит тот или другой вывод? Какими фактами они обоснованы?».
В данной истории военные предполагали, что вернувшиеся воздушные судна – это случайная выборка из общего количества, но, когда приходит осознание об ошибочности данного предположения, становится понятно, что нет никакого смысла ожидать объективной возможности выживания всех самолетов вне зависимости, в какую часть объекта попадает пуля. Такой вывод можно описать термином «систематическая ошибка выжившего».
Неточности и изъяны
Просчеты возникают нередко и в разных ситуациях. Аналогично, нельзя утверждать, что дельфины выталкивают уходящих под воду людей на сушу, ведь водные млекопитающие лишь поддерживают тонущего на плаву, подталкивая его в произвольном направлении. Но, лишь те, кто выжил, смогли об этом рассказать. Теория, представленная Абрахамом в середине прошлого столетия, позволила понять смысл "бесконечно малых приращений", которые, ранее, считались нелепыми. Его математический склад ума позволил избежать ненужных ошибок, и сделать шаг в правильном направлении решения поставленной задачи.
Линейная зависимость
Джордан Элленберг в «Как не ошибаться. Сила математического мышления» затрагивает сравнение развития Швеции и США, демонстрируя на графиках линейную зависимость между материальным благополучием и уровнем социальных льгот. Шведы ведут свою экономику в сторону свободного рынка, сокращая соцобеспечение, Америка же – наоборот, идет по пути увеличения его объема. В учебнике представляются графики, отражающие разницу линейности и нелинейности между странами. Автор отмечает, что мыслить нелинейно - важно, потому что не все линии являются прямыми.
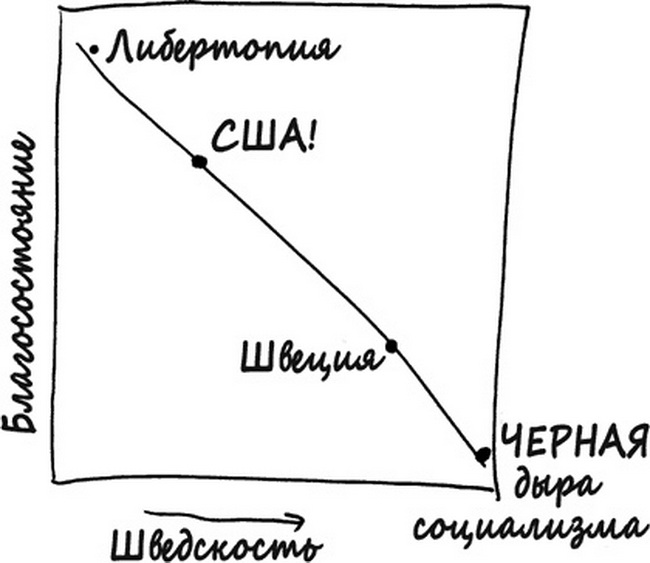
Прямая и кривая
Мыслительный процесс линейного характера встречается повсюду. Автор «Как не ошибаться. Сила математического мышления» утверждает, что каждый из нас мыслит таким образом, особенно, когда действует по принципу «если что-то имеешь, то лучше увеличивать его численность». Элленберг не понимает, как можно быть уверенным в том, что все линии прямые, когда, на его взгляд, очевидно обратное. Ньютон говорил, необходимо сокращать поле зрения, пока оно не станет максимально малой величиной, но не равной нулю.
Линейное мышление характерно для каждого человека, ведь бессознательное восприятие времени и движения формируется под воздействием внешних явлений. Еще до открытий Ньютона все подсознательно понимали, что все вокруг старается двигаться по прямой, если не появляется возможность или причина двигаться иначе.
Линейная регрессия на примере
Жанр «Как не ошибаться. Сила математического мышления» - научная литература популярного направления, где автор анализирует арифметические структуры на конкретных примерах. В главе №3 Элленберг берет за основу напечатанную в публицистическом издании статью, в которой приводилось предположение о том, что все американцы в будущем, к 2048 году, будут страдать ожирением.
Он сразу спешит успокоить американских читателей, уверяя, что данное предположение не может быть правдой, так как не все линии прямые, нельзя проектировать данную гипотезу на всех, изначально закладывая одинаковый результат. Как было сказано выше, каждая линия близка к прямой, и эта идея лежит в основе линейной регрессии.

Удача и брокер из Балтимора
«Как не ошибаться. Сила математического мышления» имеет уникальную структуру. Автор в прологе затрагивает волнующий читателей важный вопрос. Он звучит как: «Зачем мне математика?». В последующих главах он отвечает на него, показывая обширность применимости данной науки и непосредственную связь с настоящей реальностью.
В шестой главе Джордан предлагает познакомиться с притчей, благодаря которой можно представить такую ситуацию: человек получает письмо от балтиморского фондового брокера, в котором идет речь о ближайшем повышении курса определенных акций. На протяжении недели акции действительно повысились в цене. Через неделю приходит еще одно уведомление, где уже имеется информация о снижении стоимости акций, по мнению брокера. Действительно, через несколько дней акции упали. Так происходит 10 недель подряд, и каждую неделю человек получает информационное письмо от брокера с верным предсказанием.

На 11-й неделе поступает предложение от этого же брокера по инвестированию денег через него за комиссионные. Изначально не возникает сомнений, что такое вложение – неплохая сделка. Но, если подробно разобрать ситуацию, уверенность уйдет на второй план. В «Как не ошибаться. Сила математического мышления» Элленберг заставляет задуматься, и приводит доводы в пользу «за» и «против». Нельзя отрицать, что фондовый брокер из Балтимора что-то понимает в игре на бирже, ведь 10 правильных прогнозов не может сделать дилетант без знаний о рынке и акциях.
Но на самом деле каждый может рассчитать шансы на успех: если новичок дает правильный прогноз с вероятностью 50 %, тогда вероятность получения десяти правильных прогнозов подряд составит (1/2)10 = 1/1024 = 0,1 %. Если ситуацию описывать с точки зрения фондового брокера, то в первую неделю он разослал 10 240 писем: 50 % из них были с прогнозом роста акций, 50% - их падения. Половина людей, получивших письма (с неправильным предсказанием), больше не получали прогнозов, остальные же, снова получили письма по такой же схеме.
Соответственно, уже четверть от изначального количества – 2 560 человек, получили два правильных предсказания подряд. После десятой недели остается 10 человек, которые постоянно получали правильные прогнозы, именно в их глазах брокер выглядит гением. С этих десяти человек брокер планирует собрать большие комиссионные в будущем, играя на их доверии.
Нулевая гипотеза
Книга «Как не ошибаться. Сила математического мышления» разграничивает явления настоящего времени и случайные препятствия, используя общепринятые методы анализа результатов. Геометрия и арифметика, по мнению автора, соответствуют нашей интуиции. Но, вероятность – это другая сторона вопроса, как и нулевая гипотеза – мнение о том, что изучаемое влияние не имеет конечного результата.
Процедура оспаривания нулевой гипотезы основана на проведении эксперимента: выдвигается предположение, в котором нулевая гипотеза берется за истину, а вероятность обозначается символом «p». Когда значение «р» минимальное, то можно предположить, что полученные факты имеют важное значение. Если значение большое, то факт остается фактом: ошибочность нулевой гипотезы не была доказана.
Гаруспиция
В девятой главе «Как не ошибаться. Сила математического мышления» описывается история, рассказанная Шализи. Автор предлагает читателям представить себя в качестве гаруспика – предсказателя, который понимает характер грядущих происшествий по потрохам овцы, зарезанной ради науки. Все имеющиеся статистические результаты отправляются в издание о международной гаруспиции, где опубликованные данные проходят диагностику на правдивость, в соответствии со статистической значимостью.
Элленберг говорит, что не верит в псевдонауку и считает, что животные ничего не могут предсказывать, и, верные предсказания являются лишь случайным совпадением. Считая гаруспицию надувательством, Джордан уверен, что, если нулевая гипотеза всегда истина, то результаты только 1/20 экспериментов могут быть обнародованы, не смотря на это, данная статистика поддерживает веру определенного количества людей в странную науку.

Сформированное мнение о книге
Отзывы о «Как не ошибаться. Сила математического мышления» встречаются исключительно положительные. Читатели отмечают, что написать популярное издание об этой науке практически не возможно, но это сделал Элленберг. Многие открывают для себя книгу, как интересное и захватывающие пособие о математической науке. Не редко отмечают тонкое чувство юмора автора, что делает книгу еще более привлекательной.
Автор книги старался писать текст в доступной форме, чтобы у каждого читающего не возникало трудностей в понимании мысли. Элленберг демонстрирует графики, таблицы, формулы, но все в доступной, для понимания, форме.



























