Производная дроби - важная тема в математическом анализе. Она позволяет найти скорость изменения функции в данной точке. Давайте разберемся, как вычисляется производная дроби и где это применяется на практике.
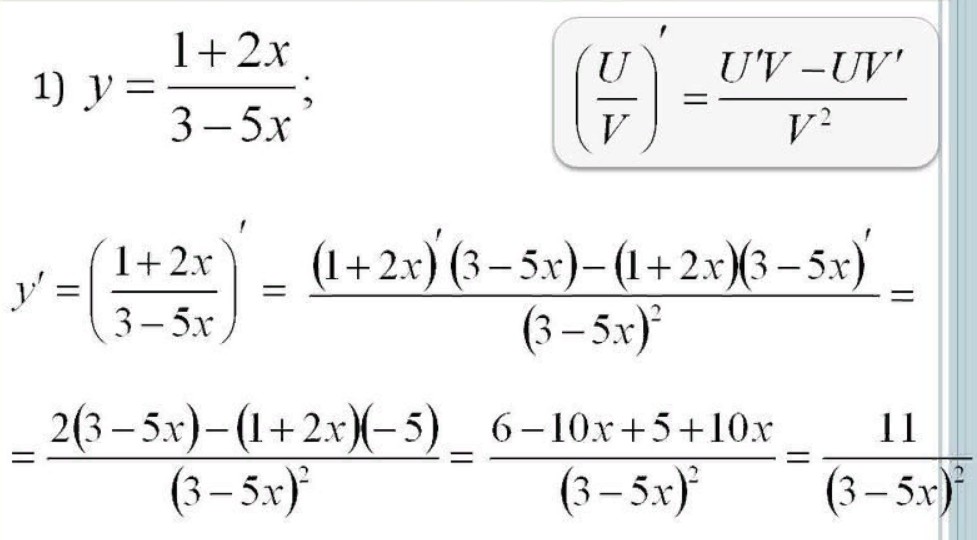
Это и есть производная нашей функции в общем виде. Как видно из формулы, производная дроби равна дроби. А числитель этой дроби находится по правилам дифференцирования суммы и произведения.
Где применяется производная дроби
Теперь давайте посмотрим, где может пригодиться умение находить производную дроби. Вот несколько примеров:
- В физике для нахождения скорости при неравномерном движении.
- В оптимизации - чтобы найти точки экстремума дробно-рациональной функции.
- В экономике при анализе предельных издержек, доходов, прибыли.
- В теории вероятностей для нахождения плотности распределения случайной величины.
Как видите, умение дифференцировать дроби пригодится в самых разных областях. Это важный математический навык.

Пошаговый алгоритм нахождения производной дроби
Чтобы без ошибок находить производную дроби, можно использовать следующий пошаговый алгоритм:
- Записать исходную функцию в виде дроби f(x) = g(x) / h(x)
- Найти производные числителя и знаменателя: (g(x))' и (h(x))'
- Подставить все в формулу: (f(x))' = (g(x))' * (h(x)) - g(x) * (h(x))'
- Упростить полученное выражение
Следуя этим простым шагам, вы точно не ошибетесь в вычислениях. Со временем этот алгоритм будет выполняться автоматически.
Полезные советы
В заключение давайте перечислим несколько полезных советов для работы с производными дробей:
- Проверяйте в конце, чтобы знаменатель дроби не обращался в ноль.
- Если есть вложенные дроби, дифференцируйте их по отдельности.
- При длинных вычислениях стоит промежуточные шаги записывать.
- График функции может подсказать, где стоит искать точки экстремума.
Используя эти советы и пошаговый алгоритм, вы без труда будете находить производные сложных дробей. Успехов в изучении этой важной темы!

Использование производной дроби для исследования функции
Одно из важных применений производной дроби - это исследование свойств функции. Чтобы найти точки экстремума, промежутки монотонности, точки перегиба, асимптоты функции, необходимо воспользоваться ее производной.
Например, для нахождения точек максимума и минимума функции нужно решить уравнение ее производной, приравняв ее к нулю. Точки, в которых производная равна нулю и меняет знак, будут точками экстремума.
Если производная функции положительна на некотором промежутке, то сама функция возрастает. А если производная отрицательна, то функция убывает. Это позволяет определить промежутки монотонности.
Применение производной дроби в оптимизационных задачах
Производная дроби часто используется при решении оптимизационных задач - когда нужно найти наибольшее или наименьшее значение некоторой функции.
Например, необходимо максимизировать прибыль, минимизировать издержки производства, оптимизировать скорость химической реакции и так далее. Для нахождения оптимального значения параметра составляется целевая функция и находятся ее стационарные точки.
Применение производной дроби в экономике
В экономических расчетах производные дроби позволяют находить предельные величины - предельную выручку, предельную стоимость, предельную полезность. Это важно для анализа микроэкономических процессов.
Например, для нахождения оптимального объема производства используют понятие предельного дохода - дохода от производства дополнительной единицы продукции. Это позволяет максимизировать прибыль.
Применение производной дроби в физике
В физических задачах производная дроби позволяет описывать скорость и ускорение при неравномерном движении. Например, если зависимость координаты от времени задана дробно-рациональной функцией.
Производная в этом случае дает скорость в данный момент времени. А производная от скорости - ускорение. Это помогает полностью описать динамику движения тела.
Применение производной дроби в теории вероятностей
Еще одна важная область применения производных дробей - это теория вероятностей и математическая статистика. Производная от функции плотности вероятности f(x) позволяет найти функцию распределения случайной величины F(x).
Это особенно удобно, когда плотность вероятности задана в виде дробно-рациональной функции. Тогда, найдя ее производную, можно получить распределение в явном виде.
Приближенные методы вычисления производной дроби
Помимо точного аналитического вычисления, для нахождения производной дроби можно использовать численные методы. Это актуально, когда дробь слишком сложная для дифференцирования.
Например, метод конечных разностей позволяет найти численное приближение производной в некоторой точке по значениям самой функции в этой и соседних точках.
Производная дроби в компьютерных вычислениях
В программировании производные дробей могут использоваться для реализации численных методов оптимизации, решения дифференциальных уравнений, статистического анализа данных.
Для этого в языках программирования реализованы специальные математические библиотеки, позволяющие эффективно вычислять производные сложных дробно-рациональных выражений.
История открытия производной
Понятие производной было введено в математический анализ постепенно. Первые идеи дифференциального исчисления появились в трудах Исаака Ньютона и Готфрида Лейбница в XVII веке.
Они рассматривали производную как скорость изменения функции и использовали ее для изучения движения небесных тел. Далее теория дифференциального исчисления была существенно развита математиками последующих поколений.

























