Подстановки Эйлера - мощный математический инструмент с удивительной историей. Хотите узнать, как с их помощью решать сложные интегралы и уравнения? Тогда эта статья для вас!
1. История создания теории подстановок Эйлера
Великий швейцарский математик Леонард Эйлер в 1748 году опубликовал работу «Введение в анализ бесконечных», где впервые описал особый метод преобразования интегралов и дифференциальных уравнений. Этот метод получил название подстановок Эйлера. До этого математики сталкивались с большими трудностями при вычислении интегралов, содержащих в подынтегральном выражении корень из многочлена.
Например, интеграл вида ∫(x+√(x2+1))-1dx казался практически невычислимым в то время. Подстановки Эйлера позволили свести такие интегралы и дифференциальные уравнения к более простым, которые уже умели решать. Это открытие сыграло огромную роль в развитии математического анализа.
2. Сущность подстановок Эйлера
Подстановки Эйлера представляют собой замену переменной интегрирования с помощью специальных формул. Рассмотрим эти формулы подробнее:
- Если a > 0, то
√(ax2+bx+c)=±√ax±t - Если c > 0, то
√(ax2+bx+c)=x±√c∓t/x - Если квадратный трехчлен имеет два действительных корня x1 и x2, то
√(ax2+bx+c)=±√(x-x1)(x-x2)±t
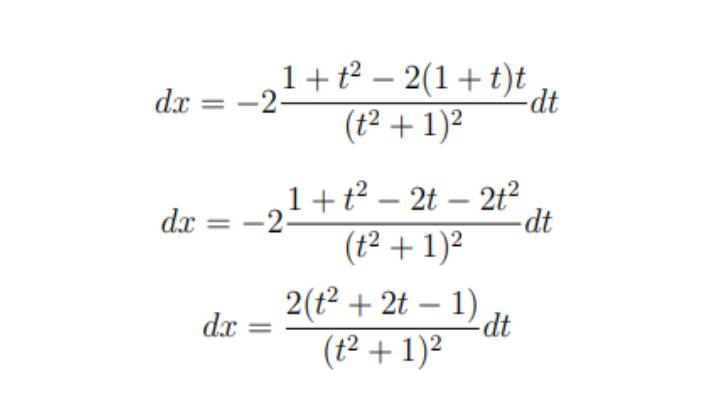
Таким образом, мы выражаем переменную x и корень из многочлена через некоторую новую переменную t. Подставляя полученные выражения в исходный интеграл или уравнение, мы преобразуем их к более простому виду.
Например, для интеграла ∫(2x+√(x2+4))-1dx воспользуемся первой подстановкой Эйлера, так как коэффициент при x2 больше нуля. Получим √(x2+4)=√2x+t. Выразим x через t, подставим в интеграл и проинтегрируем. В результате интеграл вычислен!
Подстановки Эйлера - применение
Помимо неопределенного интегрирования, подстановки Эйлера используются при решении:
- Дифференциальных уравнений
- Задач оптимизации
- Уравнений математической физики
Одна из важнейших областей применения - это интегралы, не берущиеся в элементарных функциях. Например:
∫ex√(a+bx)ndx(a, b, n - постоянные)
Такие интегралы берутся лишь при определенных значениях показателя степени n. С помощью подстановок Эйлера этот интеграл можно свести к виду ∫P(t)eQ(t)dt, где P(t) и Q(t) многочлены. Теперь интеграл берется для любых значений n, что очень удобно в приложениях.
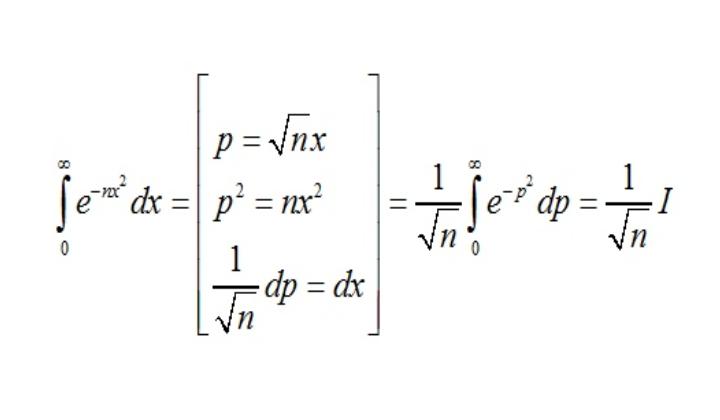
Далее рассмотрим более подробно применение подстановок Эйлера в интегрировании и решении дифференциальных уравнений.
3. Интегрирование рациональных функций
Одно из основных применений подстановок Эйлера - это интегрирование рациональных функций, содержащих корень из многочлена. Например, рассмотрим интеграл
∫(3x+√(x2+5x+6))-1dx
Здесь в подынтегральном выражении присутствует корень из квадратного трехчлена. Разложим его на множители: x2+5x+6=(x+2)(x+3). Применим подстановку Эйлера для двух действительных корней:
√(x2+5x+6)=√(x+2)(x+3)=√(x-(-2))(x-(-3))=2+t
Далее находим x=t2-5t+3 и dx=(2t-5)dt. Подставляем в исходный интеграл и получаем:
∫(2t+3(t2-5t+3)+2+t)-1(2t-5)dt
Этот интеграл вычисляется напрямую. Таким образом, подстановка Эйлера позволила свести сложный интеграл к простому виду.
4. Подстановка Эйлера - примеры для тригонометрических функций
Подстановки Эйлера успешно применяются при интегрировании тригонометрических функций. Рассмотрим классический пример:
∫tg(√(a2+x2))dx, где a - const > 0
Здесь в подынтегральном выражении under корень попадает квадратный трехчлен с положительным коэффициентом при x2. Применим первую подстановку Эйлера:
√(a2+x2)=a+t
Далее находим x=√(t2-2at) и подставляем в исходный интеграл. Получаем интеграл от рациональной функции, который берется в элементарных функциях.
Подстановки Эйлера - примеры решения дифференциальных уравнений
Еще одна важная область применения - это решение дифференциальных уравнений вида:
y ́ ́+p(x)y ́+q(x)y=0
Здесь функции p(x) и q(x) могут содержать под знаком корня многочлен. С помощью подстановок Эйлера такие уравнения иногда удается свести к уравнениям Эйлера или к уравнениям с рациональными коэффициентами.
Например, уравнение y ́ ́+(3x+√x)y ́+xy=0 после замены переменной √x=t приводится к виду y ́ ́+3ty ́+t2y=0. Это уравнение Эйлера, для которого известны методы решения. Таким образом, подстановка Эйлера позволила существенно упростить исходное дифференциальное уравнение.
5. Обобщение подстановок Эйлера на случай радикалов степени n
В ряде случаев в подынтегральных выражениях и дифференциальных уравнениях встречаются радикалы более высоких степеней. Например, корень третьей степени √[3](x3+ax+b).
Для таких случаев можно обобщить подстановки Эйлера. Делается это путем разложения радикала на множители с помощью решения соответствующего алгебраического уравнения и последующей замены одного из множителей на новую переменную.
Такой подход позволяет расширить область применения подстановок Эйлера и охватить более широкий класс интегралов и дифференциальных уравнений.

























