Медианы треугольника - важнейшие элементы, позволяющие решать множество задач. Давайте разберемся в удивительных свойствах медиан и научимся использовать их на практике.
Свойства медиан треугольника
Медианой треугольника называется отрезок, соединяющий вершину треугольника с серединой противоположной стороны. В любом треугольнике можно провести ровно три медианы:
- Медиана
AMсоединяет вершинуAс серединой стороныBC - Медиана
BNсоединяет вершинуBс серединой стороныAC - Медиана
CKсоединяет вершинуCс серединой стороныAB
Основное утверждение о медианах треугольника формулируется следующим образом:
Теорема о медианах треугольника: Все три медианы треугольника пересекаются в одной точке, которая называется центроидом. Каждая медиана делится центроидом в отношении 2:1, считая от вершины.
Доказательство этого утверждения опирается на тот факт, что если соединить точки пересечения двух медиан треугольника с серединами третьей стороны, то получится параллелограмм. А в параллелограмме диагонали всегда делятся точкой пересечения пополам.
Из теоремы о медианах вытекает несколько важных следствий:
- Медианы делят площадь треугольника пополам
- В равнобедренном треугольнике медиана, проведенная к основанию, совпадает с биссектрисой и высотой
- В равностороннем треугольнике все три медианы равны
Теорема о медианах треугольника позволяет также вывести формулу для нахождения длины медианы через стороны треугольника. В общем виде она выглядит так:
Где a, b, c - стороны треугольника, ma, mb, mc - соответствующие медианы.
Кроме формул, из теоремы о медианах следует также, что в прямоугольном треугольнике медиана, проведенная к гипотенузе, всегда равна половине гипотенузы. А если медиана равна половине какой-либо стороны треугольника, то этот треугольник обязательно прямоугольный.
Теперь, когда мы разобрались со свойствами медиан треугольника, давайте посмотрим, как их можно применять для решения задач на практике.

Применение теоремы о медианах на практике
Знание теоремы о медианах треугольника позволяет решать множество практических задач, в которых требуется найти различные элементы треугольника. Давайте рассмотрим несколько примеров.
Примеры задач на медианы треугольника
Вот типичная задача на применение теоремы о медианах:
В треугольнике ABC известно, что AC = 10 см, BC = 8 см. Найдите длину медианы AM, проведенной из вершины A.
Решение:
- Записываем формулу для вычисления медианы:
ma= √(2b2 + 2c2 - a2)/2 - Подставляем значения сторон:
ma= √(2·82 + 2·102 - 102)/2 = √(128 + 200 - 100)/2 = √228/2 = 6 см
Ответ: длина медианы AM равна 6 см.
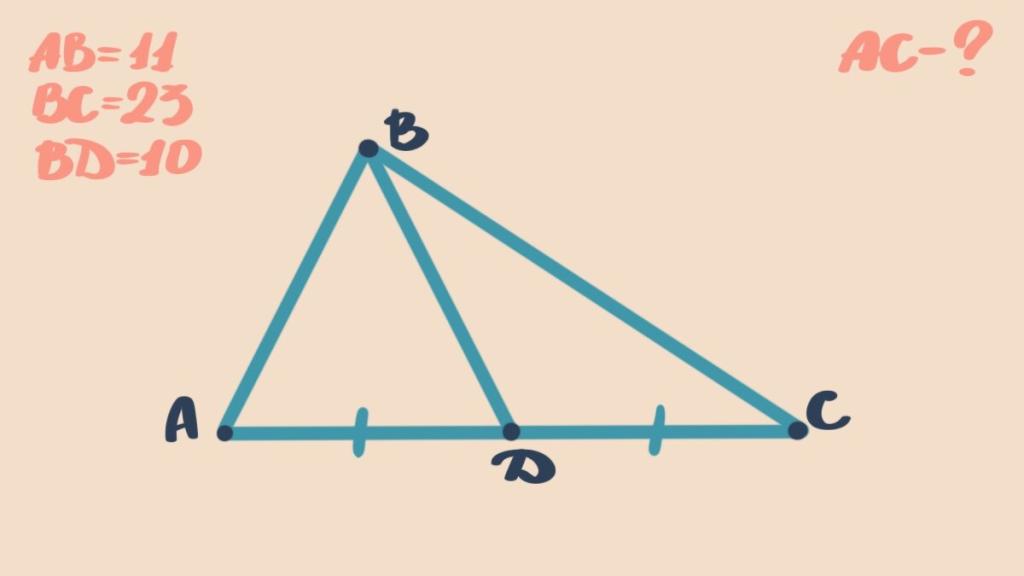
Задачи о медианах треугольника из ЕГЭ
В экзаменационных билетах ЕГЭ также встречаются задачи, связанные с медианами треугольников. Рассмотрим пример:
В треугольнике ABC известно, что BC = 4 см, AC = 6 см. Найдите площадь этого треугольника, если его медиана AM равна 3 см.
Поскольку дана медиана AM, нам известно, что треугольник ABC прямоугольный и AM является медианой, проведенной к гипотенузе AC. Тогда по теореме о медианах AM = AC/2. Отсюда находим, что AC = 2·AM = 2·3 = 6 см. Далее применяем теорему Пифагора: AB2 + BC2 = AC2. Подставляя значения, получаем: AB = √(62 - 42) = √36 - 16 = √20 = 4√5 см. Находим площадь треугольника по формуле S = (AB·BC)/2 = (4√5·4)/2 = 8 см2.
Ответ: 8 см2.
Как найти медиану реального треугольника
Теорию о медианах можно применить не только к абстрактным треугольникам в задачах. Она позволяет находить медианы вполне реальных объектов.
Например, вы хотите найти медианы треугольника, образованного тремя вершинами вашего участка. Для этого:
- Измерьте длины всех трех сторон треугольника
- Отметьте середины каждой стороны
- Соедините точки, соответствующие вершинам треугольника, с серединами противоположных сторон
Полученные отрезки и будут искомыми медианами данного треугольника!
Где в жизни пригодится знание о медианах
Кроме чисто геометрических задач, теория о медианах применима и в других областях:
- В статистике понятие медианы используется для описания распределения данных
- В экономике и финансах медиану часто применяют для анализа цен и доходов
- В социологии медианный показатель позволяет оценить типичные характеристики изучаемых групп
Таким образом, умение оперировать понятием "медиана" выходит далеко за рамки школьной программы по геометрии и может пригодиться в самых разных сферах!























