Теорема о смежных углах является одной из базовых в геометрии. Она позволяет решать множество задач, доказывать другие утверждения и теоремы. Давайте разберемся, что это за теорема и почему она так важна.
Определение смежных углов
Начнем с определения. Смежными называются два угла, у которых:
- есть одна общая сторона
- остальные две стороны являются продолжением друг друга
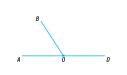
Другими словами, смежные углы лежат на одной прямой, имея общую вершину и общую сторону. Рассмотрим на чертеже:
Здесь углы АОВ и ВОС являются смежными: у них общая сторона ОВ, а стороны АО и ОС представляют собой продолжение друг друга.
Формулировка теоремы о смежных углах
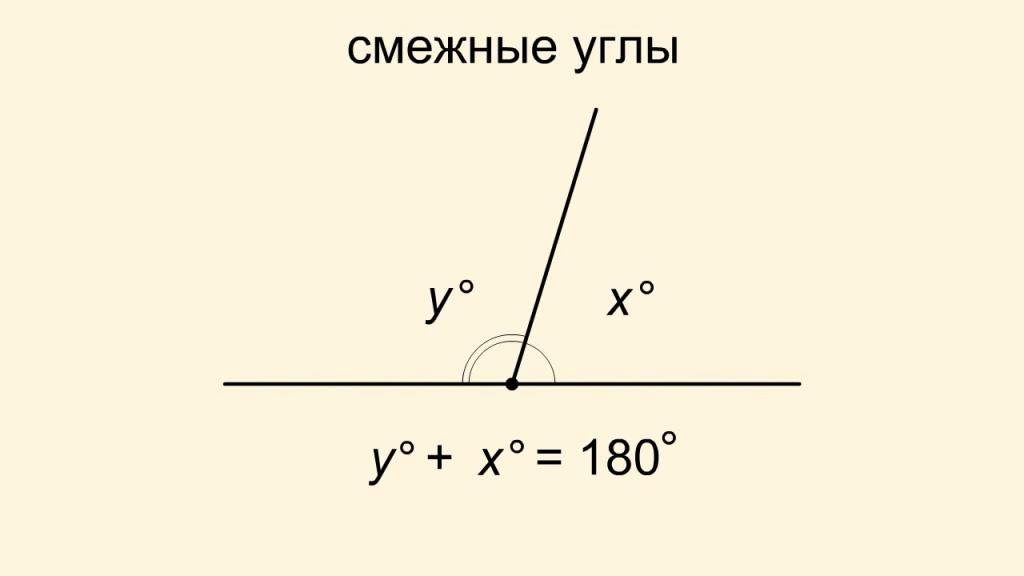
Сумма смежных углов равна 180°.
Это очень важное и фундаментальное утверждение в геометрии. Давайте докажем его.
Доказательство теоремы о смежных углах
Рассмотрим смежные углы ∠АОВ и ∠ВОС с общей стороной ОВ. Проведем через вершину О прямую, проходящую через точки А и С. Получится развернутый угол ∠АОС, равный 180° по определению развернутого угла.
Теперь заметим, что углы ∠АОВ и ∠ВОС в сумме как раз и составляют весь развернутый угол ∠АОС. Следовательно, справедливо равенство:
Теорема о смежных углах доказана.
Как видите, доказательство теоремы опирается на простейшие аксиомы и свойства углов в геометрии. Несмотря на простоту, это очень сильный инструмент для решения множества задач.
Например, если известно, что угол ∠АОВ равен 40°, то смежный с ним угол ∠ВОС легко найти как 180° - 40° = 140°. И так далее.

Применение теоремы о смежных углах
Теорема о смежных углах широко используется при решении задач и доказательстве других утверждений в геометрии. Рассмотрим несколько примеров.
Нахождение угла по смежному
Если известна величина одного смежного угла, то величину другого можно найти, используя тот факт, что их сумма равна 180°.
Например, если ∠AOB = 50°, а ∠BOC смежный с ним, то ∠BOC = 180° - 50° = 130°. И наоборот, если бы было известно, что ∠BOC = 100°, то мы нашли бы ∠AOB как 180° - 100° = 80°.
Доказательство равенства углов
С помощью теоремы о смежных углах можно доказывать равенство некоторых углов.
Например, если угол AOB смежный с углами BOC и BOD, причем ∠BOC = ∠BOD, то из теоремы о смежных углах получаем:
- ∠AOB + ∠BOC = 180°
- ∠AOB + ∠BOD = 180°
Отсюда, приравнивая правые части, получаем равенство ∠BOC = ∠BOD. Углы равны, что и требовалось доказать.
Применение при построении углов
Зная величину одного угла и используя теорему о смежных, можно строить углы заданной величины. Например, чтобы построить угол в 120°, достаточно:
- Построить произвольный угол
- Построить смежный угол к нему (они в сумме дадут 180°)
- Получившийся смежный угол и будет равен 120°
Доказательство свойств вертикальных углов
Используя теорему о смежных углах, можно строго доказать, что вертикальные углы равны. А также вывести другие их свойства.
Это лишь некоторые примеры применения теоремы о смежных углах. Она используется повсеместно в геометрии для решения самых разных задач и доказательств.
Следствия из теоремы о смежных углах
Из теоремы о смежных углах вытекает несколько важных следствий, которые также активно применяются на практике.
Если углы равны, то и смежные с ними углы равны
Это следует непосредственно из свойств смежных углов. Рассмотрим углы на чертеже:
Здесь ∠1 = ∠3, так как указано в условии. Угол ∠2 смежный с углами ∠1 и ∠3. Значит, по теореме о смежных:
- ∠1 + ∠2 = 180°
- ∠3 + ∠2 = 180°
Приравнивая правые части этих равенств, получаем, что ∠4 = ∠2. Углы равны, что и требовалось доказать.
Если угол прямой, то и смежный с ним угол прямой
Прямой угол равен 90°. По теореме о смежных два смежных угла в сумме дают 180°. Следовательно, если один из смежных углов равен 90°, то и второй должен быть равен 90°. Иначе их сумма не будет равна 180°.
Неразвернутый угол меньше 180°
Под неразвернутым понимается угол, меньший развернутого (180°). И здесь опять помогает теорема о смежных:
Пусть дан неразвернутый угол ∠AOB. Построим произвольный луч, исходящий из точки O, который образует некоторый угол ∠BOC смежный с исходным углом ∠AOB.
Тогда ∠AOB + ∠BOC = 180° по теореме о смежных углах. Но угол ∠AOB по условию меньше развернутого, значит меньше 180°. Следовательно, в равенстве ∠AOB + ∠BOC = 180° правая часть больше левой. Значит, неразвернутый угол ∠AOB действительно меньше 180°, что и требовалось доказать.