Параллелограмм - одна из самых интересных фигур в геометрии. Хотя на первый взгляд она кажется обычным четырехугольником, у параллелограмма есть много уникальных и полезных свойств.
В этой статье мы подробно разберем, что такое параллелограмм, его определение и основные признаки. Особое внимание уделим диагоналям параллелограмма и докажем, что они равны. Также узнаем, как вычислить площадь и периметр этой фигуры.
Готовы окунуться в мир удивительных свойств параллелограмма? Тогда приступим!
Что такое параллелограмм: определение
Параллелограмм - это четырехугольник, у которого противоположные стороны попарно параллельны и равны. Это одна из основных фигур в геометрии, обладающая интересными свойствами.
Параллелограмм относится к выпуклым четырехугольникам, то есть четырехугольникам, у которых все внутренние углы острые или прямые. У параллелограмма сумма всех внутренних углов равна 360°.
Параллелограмм часто встречается в архитектуре и дизайне. Например, его форма используется при проектировании зданий, элементов ландшафтного дизайна, различных конструкций.
Среди параллелограммов можно выделить несколько специальных случаев: прямоугольник, ромб и квадрат. Эти фигуры также обладают свойствами параллелограмма, но имеют и свои отличительные особенности.
В этой статье мы подробно разберем, что представляет собой параллелограмм, изучим его основные свойства и проведем интересные доказательства, связанные с диагоналями параллелограмма (диагонали параллелограмма равны).

Основные признаки параллелограмма
Параллелограмм имеет три основных признака. Если четырехугольник удовлетворяет хотя бы одному из них, то он является параллелограммом.
- Если противоположные стороны четырехугольника равны и параллельны, то это параллелограмм.
- Если противоположные стороны четырехугольника равны, то это параллелограмм.
- Если диагонали четырехугольника пересекаются в середине, то это параллелограмм.
Доказательство каждого из этих утверждений основано на построении вспомогательных элементов, таких как диагонали, и дальнейшем сравнении получившихся треугольников. Благодаря равенству треугольников по каким-либо признакам делается вывод о параллельности и равенстве противоположных сторон четырехугольника.
| Признак | Что доказывает |
| Равные и параллельные противоположные стороны | Остальные противоположные стороны тоже параллельны и равны |
| Равные противоположные стороны | Противоположные стороны параллельны |
| Диагонали, пересекающиеся в середине | Стороны параллельны и равны |
Таким образом, достаточно установить выполнение хотя бы одного из этих критериев, чтобы назвать четырехугольник параллелограммом и воспользоваться его свойствами, включая равенство диагоналей.
Диагонали параллелограмма и их свойства
Диагональ параллелограмма - это отрезок, соединяющий две противоположные вершины параллелограмма. У диагоналей параллелограмма есть несколько интересных свойств.
- Диагонали параллелограмма пересекаются в своей середине. Это значит, что точка их пересечения делит каждую диагональ на два равных отрезка. Это свойство позволяет использовать диагонали как биссектрисы углов параллелограмма.
- Диагонали параллелограмма равны. Это удивительное свойство вытекает из равенства треугольников, на которые диагонали разбивают параллелограмм.
- Каждая диагональ делит параллелограмм на два равных треугольника. Стороны этих треугольников попарно равны, а углы тоже равны соответствующим углам другого треугольника.
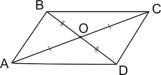
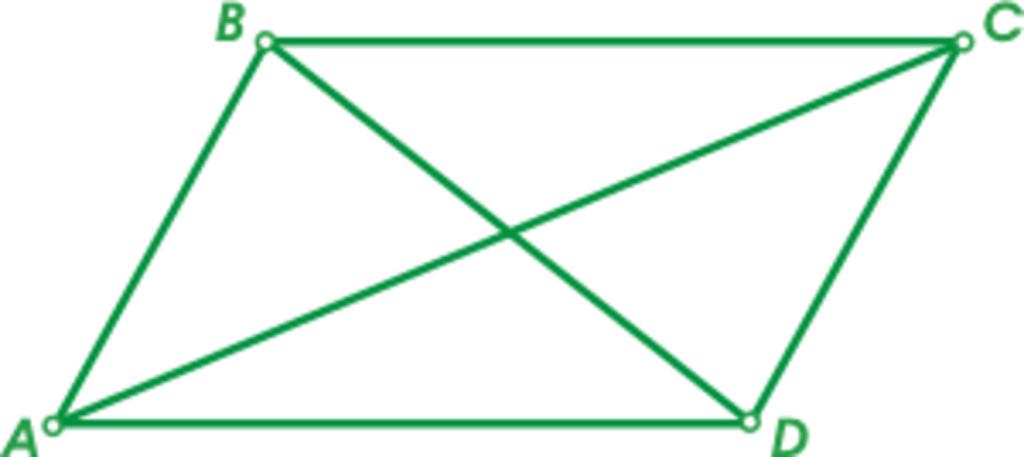
Доказать равенство диагоналей параллелограмма можно следующим образом. Рассмотрим произвольный параллелограмм ABCD. Проведем в нем обе диагонали AC и BD. Они пересекаются в некоторой точке O. Теперь сравним треугольники AOB и COD, образованные этими диагоналями с вершинами параллелограмма.
У этих треугольников:
- AB = CD как противоположные стороны параллелограмма;
- ∠AOB = ∠COD как вертикальные углы;
- AO = CO по конструкции диагоналей, пересекающихся в середине.
Значит, треугольники равны по трем элементам - трем сторонам. Согласно признаку равенства треугольников следует, что остальные элементы треугольников тоже равны, в частности, OB = OD. Но OB и OD - это части диагоналей AC и BD, причем равные части. Поэтому сами диагонали равны, AC = BD.
Таким образом, диагонали параллелограмма равны. Это универсальное свойство выполняется для любого параллелограмма и является еще одним его важным признаком, помимо равенства и параллельности противоположных сторон.
Из равенства диагоналей следует интересный геометрический факт: если в произвольном выпуклом четырехугольнике провести диагонали так, что они разделятся пополам, то такой четырехугольник обязательно будет параллелограммом. Это можно использовать как определение параллелограмма или как его признак - третий из основных.
Еще одно следствие свойств диагоналей - деление параллелограмма на равновеликие треугольники. Как мы выяснили, треугольники AOB и COD, образованные диагоналями, равны. Но их площади в сумме дают площадь самого параллелограмма:
S△AOB + S△COD = SABCD
Поэтому площадь параллелограмма равна удвоенной площади каждого такого треугольника. А это значит, что каждая диагональ делит параллелограмм на два равновеликих треугольника. И это тоже важное свойство параллелограмма.
Таким образом, неслучайно диагонали называют важнейшими линиями параллелограмма. Они задают его форму, делят на равные части, позволяют вычислять площадь. И конечно же, сами диагонали параллелограмма равны. Это свойство фигуры часто помогает в решении задач.
Как найти площадь и периметр параллелограмма
Параллелограмм - это четырехугольник, у которого противоположные стороны попарно параллельны. Чтобы найти площадь параллелограмма, нужно знать длины двух смежных сторон и высоту, проведенную к одной из этих сторон. Площадь параллелограмма равна произведению длины стороны на соответствующую ей высоту.
Формула для нахождения площади параллелограмма:
S = a * h
где a - длина стороны, h - высота к этой стороне.
Периметр параллелограмма равен сумме длин всех его сторон. Так как у параллелограмма противоположные стороны равны, то периметр равен:
P = 2 * (a + b)
где a и b - длины двух смежных сторон.
Таким образом, зная длины сторон параллелограмма и соответствующую высоту, можно найти его площадь и периметр.