Ряд Маклорена и разложение некоторых функций

Изучающим высшую математику должно быть известно, что суммой некоего степенного ряда, принадлежащего интервалу сходимости данного нам ряда, оказывается непрерывное и безграничное число раз дифференцированная функция. Возникает вопрос: можно ли утверждать, что заданная произвольная функция f(х) - это сумма некоего степенного ряда? То есть при каких условиях ф-ия f(х) может быть изображена степенным рядом? Важность такого вопроса состоит в том, что существует возможность приближенно заменить ф-ию f(х) суммой нескольких первых членов степенного ряда, то есть многочленом. Такая замена функции довольно простым выражением - многочленом - является удобной и при решении некоторых задач математического анализа, а именно: при решении интегралов, при вычислении дифференциальных уравнений и т. д.

Доказано, что для некой ф-ии f(х), в которой можно вычислить производные до (n+1)-го порядка, включая последний, в окрестности (α - R; x₀ + R) некоторой точки х = α справедливой является формула:

Данная формула носит имя известного ученого Брука Тейлора. Ряд, который получают из предыдущего, называется ряд Маклорена:

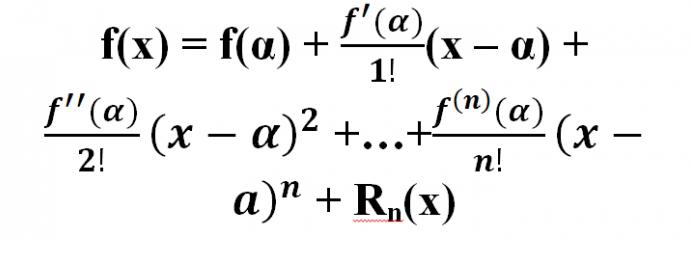
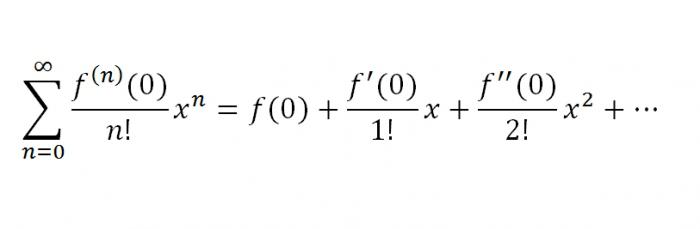
Правило, которое дает возможность произвести разложение в ряд Маклорена:

1. Определить производные первого, второго, третьего... порядков.
2. Высчитать, чему равны производные в х=0.
3. Записать ряд Маклорена для данной функции, после чего определить интервал его сходимости.
4. Определить интервал (-R;R), где остаточная часть формулы Маклорена

R_n(х) -> 0 при n -> бесконечности. В случае если таковой существует, в нем функция f(х) должна совпадать с суммой ряда Маклорена.

Рассмотрим теперь ряды Маклорена для отдельных функций.

1. Итак, первой будет f(x) = е^х. Разумеется, что по своим особенностям такая ф-ия имеет производные самых разных порядков, причем f^(k)(х) = e^x, где k равняется всем натуральным числам. Подставим х=0. Получим f^(k)(0) = e⁰=1, k=1,2... Исходя из вышесказанного, ряд е^х будет выглядеть следующим образом:

2. Ряд Маклорена для функции f(х) = sin х. Сразу же уточним, что ф-ия для всех неизвестных будет иметь производные, к тому же f^'(х) = cos х = sin(х+п/2), f^''(х) = -sin х = sin(х+2*п/2)..., f^(k)(х) = sin(х+k*п/2), где k равняется любому натуральному числу. То есть, произведя несложные расчеты, можем прийти к выводу, что ряд для f(х) = sin х будет такого вида:

3. Теперь попробуем рассмотреть ф-ию f(х) = cos х. Она для всех неизвестных имеет производные произвольного порядка, причем |f^(k)(x)| = |cos(х+k*п/2)|<=1, k=1,2... Снова-таки, произведя определенные расчеты, получим, что ряд для f(х) = cos х будет выглядеть так:

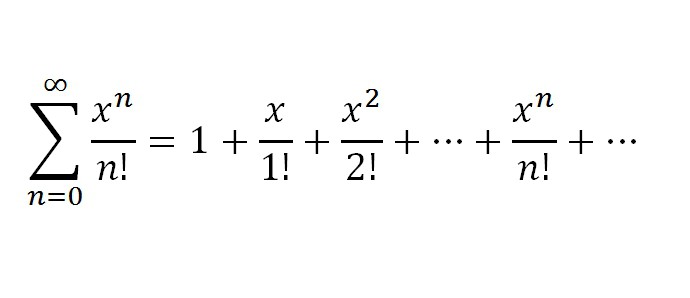
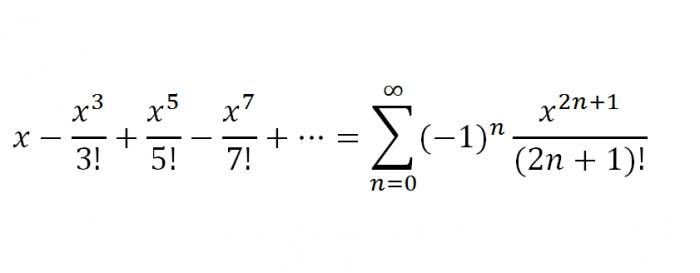
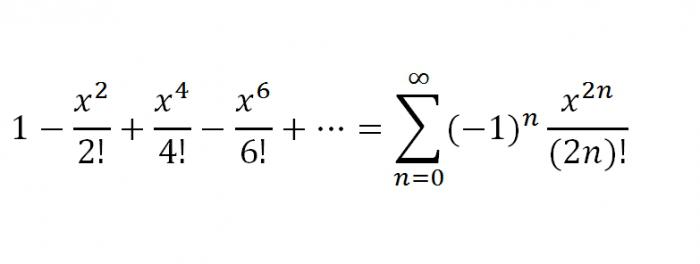
Итак, мы перечислили важнейшие функции, которые могут быть разложены в ряд Маклорена, однако их дополняют ряды Тейлора для некоторых функций. Сейчас мы перечислим и их. Стоит также отметить, что ряды Тейлора и Маклорена являются важной частью практикума решения рядов в высшей математике. Итак, ряды Тейлора.

1. Первым будет ряд для ф-ии f(х) = ln(1+x). Как и в предыдущих примерах, для данной нам f(х) = ln(1+х) можно сложить ряд, используя общий вид ряда Маклорена. однако для этой функции ряд Маклорена можно получить значительно проще. Проинтегрировав некий геометрический ряд, мы получим ряд для f(х) = ln(1+х) такого образца:

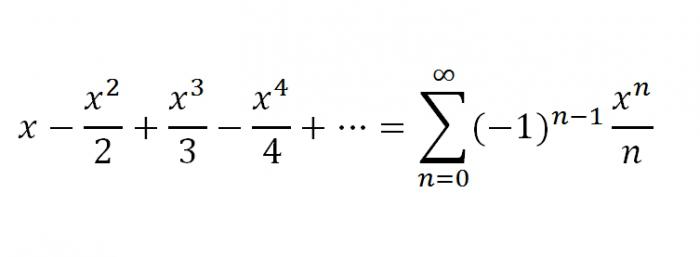
2. И вторым, который будет заключительным в нашей статье, будет ряд для f(х) = arctg х. Для х, принадлежащего промежутку [-1;1] справедливым является разложение:

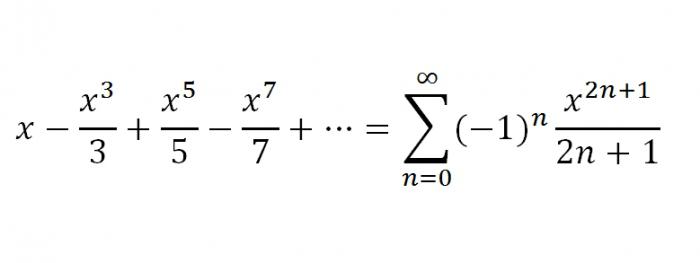
На этом все. В данной статье были рассмотрены наиболее употребляемые ряды Тейлора и Маклорена в высшей математике, в частности, в экономических и технических вузах.