Как посчитать площадь прямоугольника: практические советы

Одна из первых формул, которая изучается в математике, связана с тем, как посчитать площадь прямоугольника. Она же является и самой часто используемой. Прямоугольные поверхности окружают нас повсюду, поэтому часто требуется знать их площади. Хотя бы для того, чтобы узнать, хватит ли имеющейся в наличии краски для покраски полов.

Какие единицы измерения площади существуют?

Если говорить о той, которая принята за международную, то это будет квадратный метр. Его удобно использовать при расчете площадей стен, потолка или пола. В них указывается площадь жилья.

Когда речь идет о меньших предметах, то вводят квадратные дециметры, сантиметры или миллиметры. Последние нужны, если фигура не больше ногтя.

При измерении площади города или страны самыми подходящими оказываются квадратные километры. Но есть еще и единицы, которые используют для того, чтобы указать размер площади: ар и гектар. Первая из них еще называется соткой.

Как быть, если заданы стороны прямоугольника?

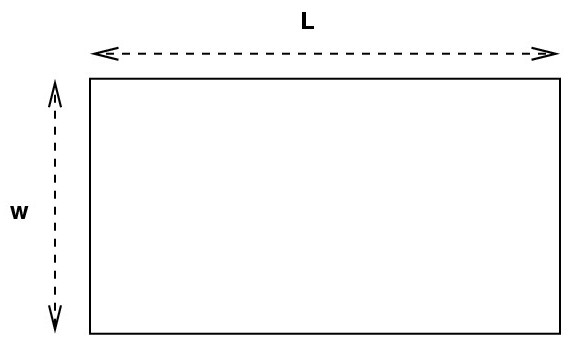
Это самый простой способ того, как посчитать площадь прямоугольника. Достаточно просто перемножить обе известные величины: длину и ширину. Формула выглядит так: S = а * в. Здесь буквами а и в обозначены длина и ширина.

Подобным образом рассчитывается площадь квадрата, который является частным случаем прямоугольника. Так как у него все стороны равны, то произведение становится квадратом буквы а.

Как быть, если фигура изображена на клетчатой бумаге?

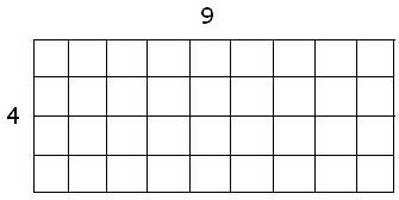
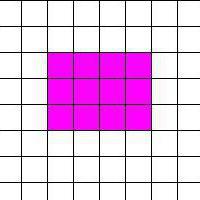
В этой ситуации нужно полагаться на количество клеточек внутри фигуры. По их числу бывает просто посчитать площадь прямоугольника. Но это можно сделать тогда, когда стороны прямоугольника совпадают с линиями клеток.

Часто имеет место такое положение прямоугольника, при котором его стороны наклонены по отношению к разлиновке бумаги. Тогда количество клеток определить сложно, поэтому расчет площади прямоугольника усложняется.

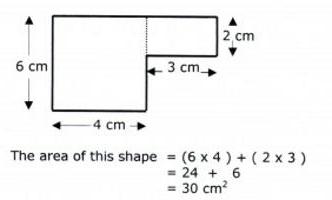
Потребуется сначала узнать площадь прямоугольника, который можно прочертить по клеточкам точно вокруг данного. Это просто: перемножить высоту и ширину. Потом вычесть из получившегося значения площади всех прямоугольных треугольников. А их четыре. К слову, их рассчитывают как половину произведения катетов.

Итоговый результат даст значение площади данного прямоугольника.

Как поступить, если стороны неизвестны, зато даны его диагональ и угол между диагоналями?

До того как находить площадь прямоугольника, в этой ситуации нужно вычислить его стороны, чтобы воспользоваться уже знакомой формулой. Поначалу потребуется вспомнить свойство его диагоналей. Они равны и делятся точкой пересечения пополам. Можно увидеть на чертеже, что диагонали делят прямоугольник на четыре равнобедренных треугольника, которые попарно равны друг другу.

Равные стороны этих треугольников определяются как половины диагонали, которая известна. То есть в каждом треугольнике есть две стороны и угол между ними, которые даны в задаче. Можно воспользоваться теоремой косинусов.

Одна сторона прямоугольника будет вычислена по формуле, в которой фигурируют равные стороны треугольника и косинус заданного угла. Для вычисления второй значение косинуса придется брать от угла, равного разности 180 и известного угла.

Теперь задача о том, как посчитать площадь прямоугольника, сводится к простому перемножению двух полученных сторон.

Что делать, если в задаче дан периметр?

Обычно в условии указывается еще и соотношение длины и ширины. Вопрос о том, как посчитать площадь прямоугольника, в этом случае проще на конкретном примере.

Допустим, что в задаче периметр некоторого прямоугольника равен 40 см. Известно также, что его длина в полтора раза больше ширины. Необходимо узнать его площадь.

Решение задачи начинается с записи формулы периметра. Его удобнее расписать как сумму длины и ширины, каждую из которых умножить на два по отдельности. Это будет первым уравнением в системе, которую потребуется решить.

Второе связано с известным по условию соотношением сторон. Первая сторона, то есть длина, равна произведению второй (ширины) и числа 1,5. Это равенство нужно подставить в формулу для периметра.

Получится, что он равен сумме двух одночленов. Первый — произведение 2 и неизвестной ширины, второй — произведение чисел 2 и 1,5 и той же ширины. В этом уравнении всего одна неизвестная — это ширина. Нужно ее сосчитать, а потом воспользоваться вторым равенством, чтобы сосчитать длину. Останется только перемножить эти два числа, чтобы узнать площадь прямоугольника.

Расчеты дают такие величины: ширина — 8 см, длина — 12 см, а площадь — 96 см². Последнее число — ответ рассмотренной задачи.