Индекс - это относительная величина, показывающая динамику исследуемого процесса (явления) как во времени, так и в пространстве, либо отражающая уровень выполнения плана. В агрегатных индексах в структурных частях формулы могут применяться арифметические операции сложения, произведения либо суммы произведений показателей исследуемых явлений или процессов.
Понятие об индивидуальных рассматриваемых объектах
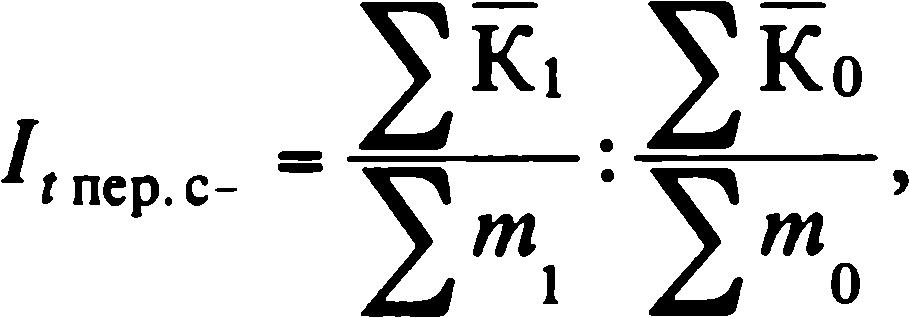
Для того чтобы прийти к понятию агрегатного индекса, нужно рассмотреть сначала, что такое индивидуальный.
Последние показывают отношение некоторых элементов какой-либо совокупности, например динамику выпуска конкретной продукции. При этом происходит сравнение величин за два периода: базисный и отчетный. Первым из них является тот, с которым производится сравнение. Отчетным называется текущий период. Они обозначаются подстрочными знаками. Базовый — 0, отчетный — 1 (если несколько отчетных периодов, то используются и последующие натуральные числа).
Количество принято обозначать q, затраты времени на изготовление единицы продукции – t, себестоимость — z, цену — р.
Исходя из этого, не агрегатный индекс объема, а индивидуальный, выражают формулой: i0 = q1/q0. Аналогичным образом, с подстановкой соответствующих значений рассчитываются индивидуальные индексы цен, себестоимость и затрат времени на изготовление единицы продукции.
Индекс товарооборота отражает динамику объема данного показателя в стоимостном выражении: ipq = p1q1/p0q0. Следовательно, динамика товарооборота происходит при изменении как объема, так и цены реализуемой продукции. В основном индексы выражают в единицах. При умножении на 100 возможен перевод в проценты.
Базисные и цепные индексы
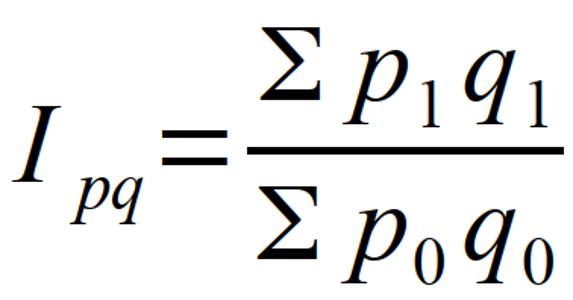
Как уже отмечалось, для определения рассматриваемых объектов должны присутствовать данные как минимум за два периода.
При существовании некоторого объема данных за определенный ряд уровней или периодов в качестве базы принимают либо начальный уровень, либо таковой по отношению к предыдущему периоду. Для первого случая получают индексы с константной базой, называемые базисными, для второго она постоянно изменяется, их называют цепными.
Первые используют для характеристики динамики некоторых процессов, происходящих в течение длительного временного периода по отношению к некоторой точке. В случае необходимости в отслеживании текущих изменений процесса используют цепные индексы.
Определение первых через вторые и наоборот осуществляется в том случае, если на их основе происходит исследование одного и того же периода.
Общие индексы
Они показывают отношение такой совокупности явлений или процессов, состоящих из элементов, которые напрямую являются несоизмеримыми. Данные индексы называют агрегатными общими индексами. Они получили наибольшее распространение в экономике.
Так, например, агрегатный индекс товарооборота приведен на рисунке 2.
Для построения любого из рассматриваемых индексов необходимо решить три вопроса:
- определиться с индексируемой величиной;
- с элементами, которые входят в состав процесса или явления, подвергающегося индексированию;
- выбрать веса.
Наиболее типичными представителями данных индексов являются агрегатный индекс физического объема, цен, стоимости.
Понятие весов
Последние представляют собой величину, которая является соизмерителем для индексируемых процессов или явлений. При расчете индекса динамика идет в отношении одноименной величины от отчетного периода к базисному, кроме индекса производительности труда по трудоемкости.
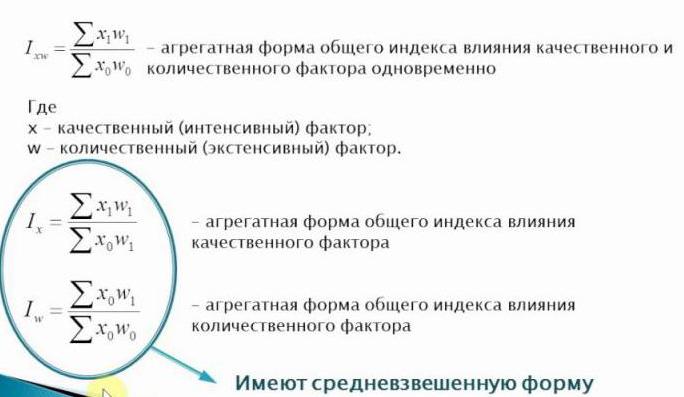
За исключением случаев, при которых величиной, подвергаемой индексированию, является все произведение, веса остаются неизменными. Первая является качественным показателем, а вторые — количественным в индексах качественных показателей, и наоборот, в таковых количественных показателей. Сводные индексы записываются таким образом, чтобы на первом месте стояла индексируемая величина, а на последнем — вес.
Выбираем постоянную величину — пример с индексом цен

Динамику цен определяют при принятии в качестве рассматриваемого количества проданных товаров за какой-то один из исследуемых временных периодов. Независимо от того, какой взят период, формулы агрегатных индексов будут выглядеть одинаково (приведены на рисунке 6). Однако считать их идентичными нельзя. Это связано с тем, что в качестве весов могут браться данные либо отчетного, либо базисного периода, что даст при расчете разные величины агрегатной формы индексов.
В случае если в их качестве принималось число реализованных товаров за отчетный период, то индекс отражает динамику цен отчетного периода в сравнении с базисным по тем товарам, реализация по которым присутствовала в отчетном периоде и демонстрирует экономию, которая могла бы иметь место, если бы цены на продукцию снизились.
В ином случае (вес — число реализованных товаров в базисном периоде) индекс отражает ту же динамику, но только в отношении той продукции, которая продавалась в базисном периоде, а также ту же самую экономию. Последняя рассчитывается как разница числителя и знаменателя агрегатного индекса. Таким образом, в данном случае переменной величиной, подвергаемой индексированию, является цена, а вес количества реализованной в отчетном периоде продукции принимается как постоянная величина.
Выбираем постоянную величину — пример с индексом объема
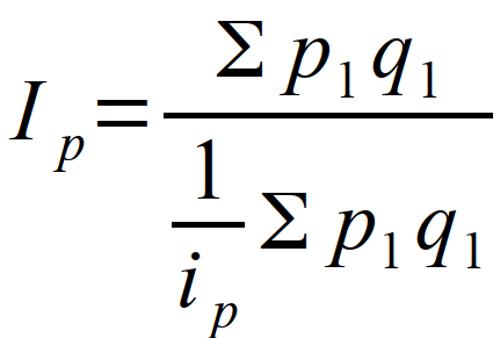
Агрегатный индекс объема товарооборота отражает динамику заложенного в названии показателя при сравнении отчетного периода с базисным. Для этого в качестве весов используются цены базисного периода. С помощью данного приема получают верное представление об изменении объема товарооборота.
Расчет данного индекса осуществляют по формуле, приведенной на рисунке 2.
Абсолютную динамику определяют по разнице числителя и знаменателя из дроби расчета. Таким образом, веса за базисный период берутся при построении количественных индексов (численности, физического объема), а за отчетный период — при построении качественных индексов (себестоимости, цены, производительности труда…).
Переменные и постоянные веса для индексов, рассчитываемых за ряд периодов
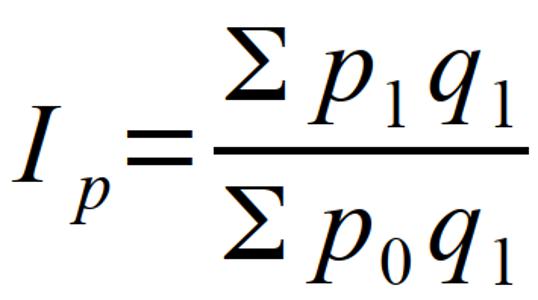
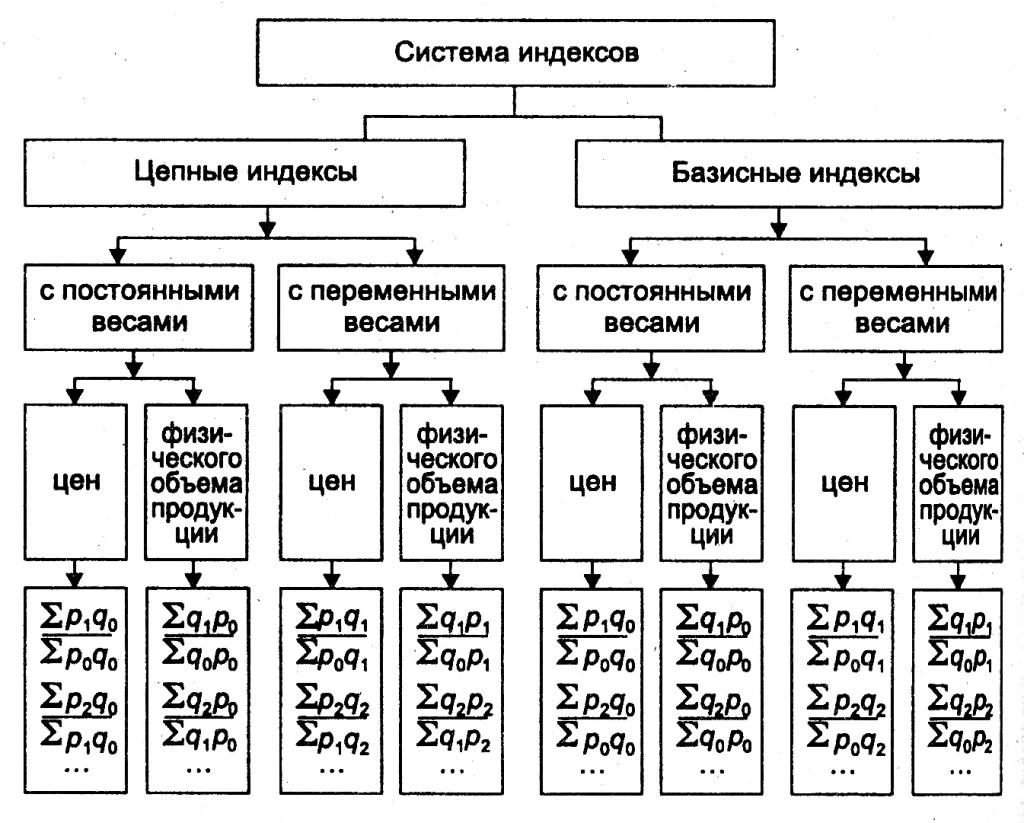
При расчете данных величин не за один, а за несколько периодов веса могут быть одинаковыми для всех (в этом случае говорят об индексах с постоянными весами), либо для каждого из них могут быть взяты свои веса (с переменными весами).
В этом случае классификацию типов индексов проводят следующим образом:
- общие базисные индексы цен с постоянными весами;
- они же с переменными весами;
- две таких же разновидности для цепных индексов.
Их получают при сопоставлении цен последующих периодов с предшествующим каждому из них, взвешенных на количество продукции, имеющей место в отчетном периоде.
Базисные индексы с постоянными весами применяются в случае необходимости анализа динамики цен, не учитывая ее в структуре изготовленных товаров. Если же учет осуществляется, то рассчитывают подобные индексы с переменными весами.
Если изучают динамику каждого периода в сравнении с предыдущим, то применяют соответствующие цепные индексы.
Понятие о среднем индексе
Не всегда информация, имеющаяся в наличии, позволяет определить агрегатные индексы. Средние в этом случае рассчитывают как среднеарифметические или среднегармонические величины. Математически они равны агрегатным и совпадают с ними по смыслу.
Величина среднеарифметического индекса будет равна агрегатному в том случае, если в качестве весов будут использоваться слагаемые знаменателя последнего. Данный индекс по отношению к физическому объему продукции определяют по формуле: Ip = (Σ lp x p0q0)/( Σ p0q0).
Среднегармонический индекс будет тождественным агрегатному в том случае, если в качестве весов будут использоваться слагаемые числителя последнего. Расчет среднегармонического индекса на примере себестоимости показан на рисунке 4.
Он рассчитывается в том случае, если в отчетном периоде не известны отдельные величины цен и количества реализуемых товаров, но известен товарооборот за данный период, а также индивидуальные индексы цен, а для расчета сводного индекса используются отчетные веса.
На величину индекса средних величин влияет динамика себестоимости продукции в каждом рассматриваемом предприятии и изменения вклада последних в общий объем производимой продукции. Если средние величины в индексах претерпевают динамику вследствие влияния индексируемых величин, а веса остаются постоянными, то данные индексы носят название постоянного состава. Изменение средних показателей с применением индексов производят после осуществления разбивки всей совокупности на траты по тем признакам, которые характеризуют структурные сдвиги. При этом вычисления выполняют для групповых средних.
Территориальные рассматриваемые показатели
Их применяют для сравнения показателей в пространстве. Если они являются двухсторонними, то любая территория может выступать в качестве сравниваемой и базисной.
Веса также могут использоваться для любого пространства. Чтобы избежать противоречивых результатов, прибегают к использованию двух способов. Первый из них предусматривает, что применяется суммарный вес реализованных товаров по двум регионам, который и будет использоваться в формуле территориального индекса цен. Другой способ предполагает учет соотношения весов в каждом из сравниваемых пространств. Вначале рассчитывают среднюю цену товаров по двум территориям, после чего эти данные подставляют в формулу и рассчитывают территориальный индекс.
Иные индексы
- Агрегатный индекс себестоимости. С его помощью демонстрируется отличие затрат на единицу продукции в сравниваемых периодах или плановым показателем. Относится к качественным индексам, поэтому веса используются отчетного периода.
- Индекс производительности труда. Представляет собой отношение затрат времени работы, необходимого для производства единицы продукции двух рассматриваемых периодов.
- Индекс трудоемкости. Он показывает динамику данного показателя в два рассматриваемых периода. Также относится к качественным показателям. Для расчета применяются отчетные веса.
В заключение
Таким образом, при расчете агрегатных индексов в числителях и знаменателях расчетных формул могут использоваться произведения, суммы или суммы произведений некоторых показателей изучаемых процессов или явлений. При расчете данных коэффициентов необходимо правильно выбрать, что будет выступать в качестве весов, для чего необходимо определить: к качественным или количественным относится рассчитываемый индекс. Существует множество подобных коэффициентов, позволяющих сопоставлять анализируемые показатели в сравниваемые периоды.



























