Планиметрия - это просто. Понятия и формулы

Ознакомившись с материалом, читатель поймет, что планиметрия - это вовсе не сложно. В статье приведена самая важная теоретическая информация и необходимые для решения конкретных задач формулы. По полочкам разложены важные утверждения и свойства фигур.

Определение и важные факты

Планиметрия - это раздел геометрии, рассматривающий объекты на плоской двумерной поверхности. Можно выделить некоторые подходящие примеры: квадрат, круг, ромб.

Среди всего прочего стоит выделить точку и прямую. Они являются двумя основными понятиями планиметрии.

Уже на них строятся все остальное, например:

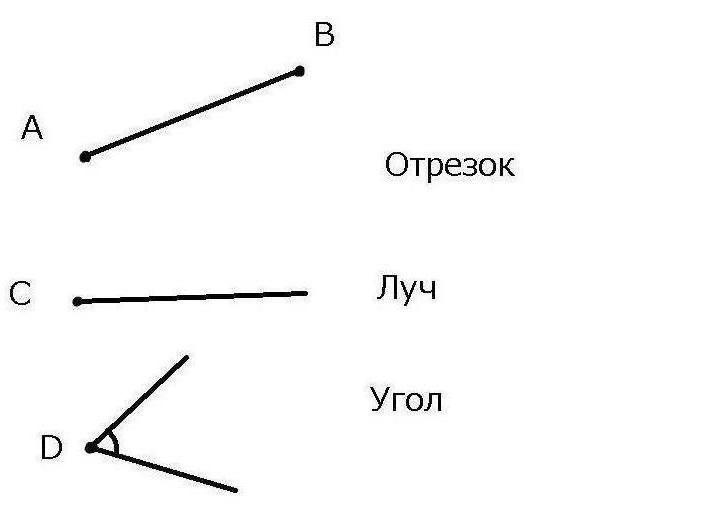
• Отрезок - часть прямой линии, ограниченная двумя точками.
• Луч - объект, аналогичный отрезку, однако, имеющий границу лишь с одной стороны.
• Угол, который состоит из двух лучей, выходящих из одной точки.
  

Аксиомы и теоремы

Подробнее разберемся с аксиомами. В планиметрии это наиважнейшие правила, по которым работает вся наука. Да и не только в ней. По определению, речь идет об утверждениях, не требующих доказательств.

Аксиомы, которые буду рассмотрены ниже, входят в так называемую Евклидовую геометрию.

• Есть две точки. Через них всегда можно провести единственную прямую.
• Если существует прямая, то есть точки, которые на ней лежат, и точки, не лежащие на ней.

Это 2 утверждения принято называть аксиомами принадлежности, а следующие – порядка:

• Если на прямой расположены три точки, то одна из них обязательно находится между двумя другими.
• Плоскость делится любой прямой на две части. Когда концы отрезка лежат на одной половине, то значит и весь объект принадлежит ей. В ином случае исходная прямая и отрезок имеют точку пересечения.

Аксиомы мер:

• Каждый отрезок имеет длину, отличную от нуля. Если точка разбивает его на несколько частей, то их сумма будет равна полной длине объекта.
• У каждого угла есть определенная градусная мера, которая не равна нулю. Если разбить его лучом, то исходный угол будет равен сумме образованных.

Параллельность:

• На плоскости расположена прямая. Через любую точку, не принадлежащую ей, можно провести лишь одну прямую, параллельную данной.

Теоремы в планиметрии - это уже не совсем фундаментальные утверждения. Обычно их принимают как факт, но каждая из них имеет доказательство, построенное на основных понятиях, упомянутых выше. Кроме того, их очень много. Разобрать все будет довольно трудно, но в представленном материале будут присутствовать некоторые из них.

Со следующими двумя стоит ознакомиться пораньше:

• Сумма смежных углов равна 180 градусам.
• Вертикальные углы имеют одинаковую величину.

Эти две теоремы могут пригодиться в решении геометрических задач, связанных с n-угольниками. Они довольно просты и интуитивно понятны. Стоит их запомнить.

Треугольники

Треугольник - это геометрическая фигура, состоящая из трех последовательно соединенных отрезков. Классифицируют их по нескольким признакам.

По сторонам (соотношения выплывают из названий):

• Равносторонний.
• Равнобедренный - две стороны и противоположные им углы соответственно равны.
• Разносторонний.
  

По углам:

• остроугольный;
• прямоугольный;
• тупоугольный.

Два угла независимо от ситуации всегда будут острыми, а третий определяется первой частью слова. То есть у прямоугольного треугольника один из углов равен 90 градусам.

Свойства:

• Чем больше угол, тем больше противоположная ему сторона.
• Сумма всех углов - 180 градусов.
• Площадь можно вычислить по формуле: S = ½ ⋅ h ⋅ a, где a - сторона, h - проведенная к ней высота.
• Всегда можно вписать окружность в треугольник или же описать ее вокруг него.

Об одной из основных формул планиметрии говорит теорема Пифагора. Работает она исключительно для прямоугольного треугольника и звучит так: квадрат гипотенузы равен сумме квадратов катетов: AB² = AC² + BC².

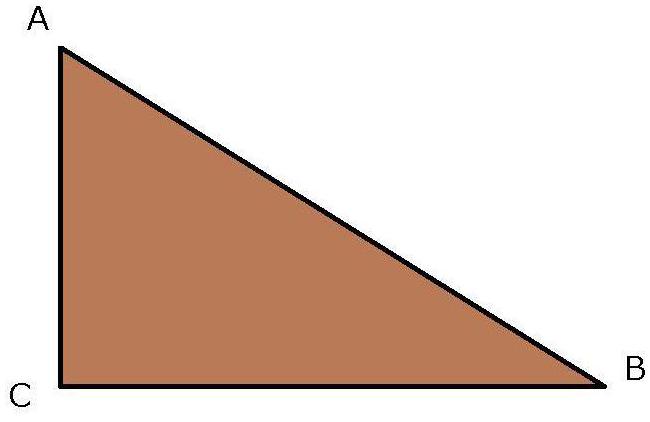
Под гипотенузой подразумевают сторону, противоположную углу 90°, а под катетами - прилежащие.

Четырехугольники

Информации на эту тему чрезвычайно много. Ниже приведена лишь самая важная.

Некоторые разновидности:

1. Параллелограмм - противоположные стороны равны и попарно параллельны.
2. Ромб - параллелограмм, чьи стороны имеют одинаковую длину.
3. Прямоугольник - параллелограмм с четырьмя прямыми углами
4. Квадрат - одновременно ромб и прямоугольник.
5. Трапеция - лишь две противоположные стороны параллельны.

Свойства:

• Сума внутренних углов равна 360 градусам.
• Площадь всегда можно вычислить по формуле: S=√(p-a)(p-b)(p-c)(p-d), где p - половина периметра, a, b, c, d - стороны фигуры.
• Если вокруг четырехугольник можно описать окружность, тогда его называю выпуклым, если нет - невыпуклым.