Экспоненциальная зависимость представляет собой математическую функцию, которая является полезной для описания процесса, где быстро увеличивается или быстро уменьшается количество каких-либо элементов. Существует множество примеров использования этой зависимости в биологии, физике, экономике, медицине и других сферах человеческой деятельности.
Определение экспоненциальной зависимости
Для того чтобы понимать, что означают слова "это количество растет экспоненциально" или "этот процесс характеризуется экспоненциальным спадом", необходимо рассмотреть понятие самой экспоненциальной функции. Для этого возьмем некоторое положительное число "a", которое не равно 1, и возведем его в степень "x", при этом переменная x может иметь как положительные, так и отрицательные значения, но не должна равняться нулю. Также возьмем некоторое постоянное число k (константа), которое не равно нулю. Теперь введем математическую функцию f(x) = k*ax. Возведение в степень "x" положительного числа "a" - это экспоненциальная зависимость, а сама функция f(x) называется показательной. В функции f(x) число "a" называется основанием, а "x" - это независимая переменная.
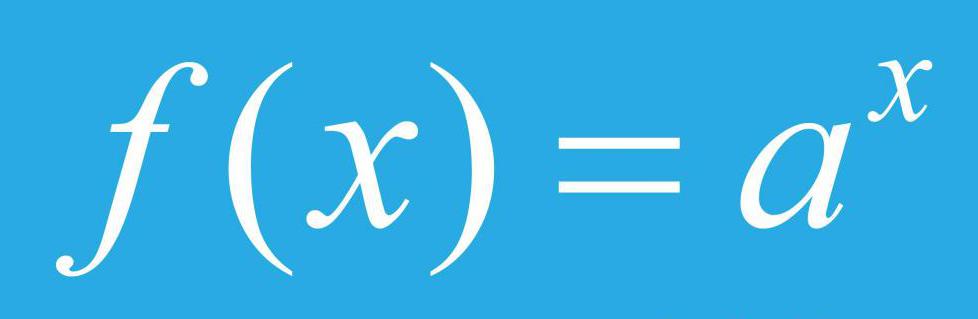
Отметим, что в математике часто фигурирует основание экспоненциальной функции "a", которое приблизительно равно 2,718. Это число обозначается латинской буквой "e" и называется числом Эйлера. Отмеченное число играет важную роль в математической теории пределов, а также во многих физических процессах в природе, например, давление воздуха с высотой на нашей планете уменьшается по экспоненциальному закону, в функциональной зависимости которого основанием выступает число Эйлера.
График экспоненциальной зависимости
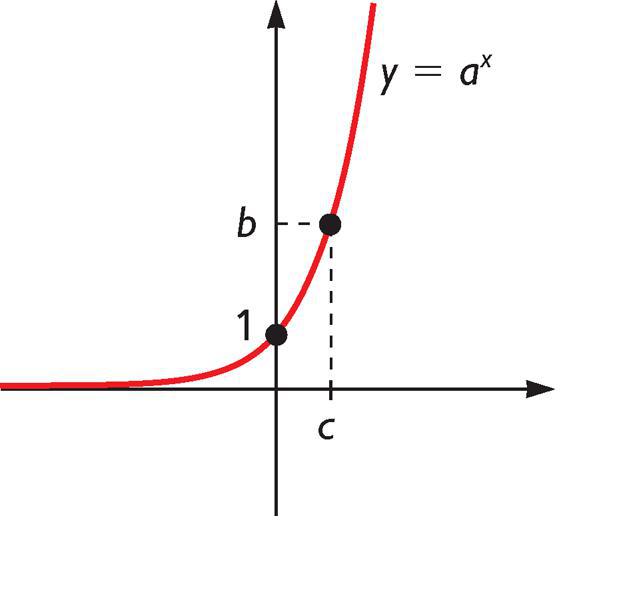
Рассмотрим свойства экспоненциальной функции y = ax, для этого обратимся к графику, представленному выше. Первым важным свойством является то, что каким бы основанием "a" ни была представлена функция, она всегда будет проходить через точку с координатами (0,1), поскольку a0 = 1.
Из графика экспоненциальной зависимости также видно, что функция ax для любых значений переменной "x" принимает только положительные значения. При больших отрицательных значениях "x" функция быстро приближается к оси абсцисс, то есть стремится к нулю. В свою очередь, уже при небольших положительных значениях "x" функция резко возрастает, при этом скорость ее увеличения постоянно увеличивается также по экспоненциальному закону, что можно показать, если взять производную от рассматриваемой функции ((ax)' = ln(a)*ax, где ln(a) - натуральный логарифм).
Таким образом, экспоненциальная зависимость - это резкое изменение некоторой величины как в сторону ее увеличения, так и в сторону уменьшения.
Пример из шахматной истории

Хорошей демонстрацией значимости экспоненциального увеличения объектов является древняя легенда, связанная с изобретением шахмат. Согласно этой легенде, для развлечения одного индусского короля, которого звали Белкиб, его близкий друг Брахман Сисса за 3000 лет до нашей эры придумал настольную игру шахматы.
Король так рад был новой игре, что пообещал дать Сиссе все, что тот пожелает. Тогда Брахман Сисса предложил ему дать столько зерна, сколько поместится на 64 шахматных клетках, при этом на 1-ю клетку он положил 1 зерно, на 2-ю - 2 зерна, на 3-ю - 4 зерна и так далее, удваивая каждый раз число. Белкиб сразу не понял, насколько много ему потребуется отдать зерна, поэтому принял без размышлений предложение своего друга.
Количество зерен, которое помещается на шахматной доске согласно описанному принципу, составит 264 = 18 446 744 073 709 551 616 - гигантское число!
Рост населения планеты
Еще одним ярким примером процессов, которые описываются согласно экспоненциальной зависимости, является рост населения планеты. Так, в 1500 году население планеты составляло около 500 млн., в 1800 году, то есть через 300 лет, оно удвоилось и стало равно 1 млрд., прошло менее 50 лет, и население планеты перешагнуло отметку 2 млрд, в настоящее время количество жителей на планете Земля составляет 7,5 млрд. человек.
Описанный на примере человечества рост популяции характерен для любого биологического вида, будь то млекопитающее или одноклеточная бактерия. Математически этот рост описывается следующей формулой: Nt = N0*ek*t, где Nt и N0 - численность популяции в моменты времени t и нулевой, соответственно, k - некоторый положительный коэффициент. Данная математическая модель роста популяций получила название экспоненциальной зависимости в экологии.
Экспоненциальный рост населения планеты заставил задуматься еще в начале XIX века известного английского экономиста и демографа Томаса Роберта Мальтуса. Ученый в свое время предсказывал, что в середине XIX века на Земле должен будет наступить голод, поскольку производство продуктов питания увеличивается линейно, в то время как численность людей на планете увеличивается экспоненциально. Мальтус полагал, что единственным способом достигнуть равновесия в рассматриваемой системе, является массовая смертность, вызванная войнами, эпидемиями и другими катаклизмами.
Как известно, ученый ошибся в своих мрачных предсказаниях, по крайней мере он ошибся с указанной датой.
Возраст археологических останков

Еще одним ярким примером природных процессов, которые происходят согласно экспоненциальному закону, является распад радиоактивных элементов. Это физическое явление, которое заключается в превращении ядер тяжелых элементов в ядра более легких, описывается следующей математической формулой: Nt = N0*e-k*t, где Nt и N0 - количество ядер более тяжелого элемента в момент времени t и в начальный момент соответственно. Из этой формулы видно, что она практически аналогична таковой для роста биологической популяции, единственное отличие заключается в знаке "минус" в показателе экспоненты, который говорит об убыли тяжелых ядер.
Отмеченную формулу используют для определения возраста горных пород и окаменелых организмов. В последнем случае работают с изотопом углерода 14C, поскольку его период полураспада (время, за которое начальное число тяжелых ядер уменьшится вдвое) является относительно небольшим (5700 лет).
Другие процессы, подчиняющиеся экспоненциальному закону
Экспоненциальная зависимость описывает многие процессы в экономике, химии и медицине. Например, дозы медикаментов, попавших в организм человека, уменьшаются во времени по экспоненциальному закону. В экономике инвестиционная прибыль, исходя из определенного начального капитала, рассчитывается также по экспоненциальному закону.



























