Графики в "Маткаде" - построение и исследование

Программа MathCAD обеспечивает стабильное поддержание своих функций уже долгие годы. В этой вычислительной среде работают экономисты, ученые, студенты и другие специалисты, владеющие прикладной и аналитической математикой. Так как математический язык понятен не всем, и не каждый способен за быстрое время его изучить, программа становится сложной для восприятия начинающих пользователей. Нагруженный интерфейс и большое количество нюансов отталкивают людей от использования этого продукта, но на самом деле разобраться в любой рабочей среде возможно - достаточно иметь желание. В этой статье разберем такую важную тему, как построение графиков функций в "Маткаде". Это несложная процедура, которая очень часто помогает при расчетах.

Типы графиков

Помимо того что в MathCAD определены быстрые графики, которые вызываются с помощью горячих клавиш, существуют и другие графические приложения. Например, пользователь может в шапке программы найти раздел "Вставка", а в ней - подраздел "График", в котором можно просмотреть все доступные графики в "Маткаде":

• График X-Y - показывает зависимость одной величины от другой. Самый распространенный тип, который позволяет быстро оценить и исследовать зависимости.
• Полярный график - использует полярные координаты. Суть графика - показать зависимость одной переменной от другой только в полярной координатной плоскости.
• График поверхности - создает поверхность в пространстве.
• Векторное поле, 3-D график разброса, столбчатая 3-D диаграмма используются для других специальных целей.

Построение графика функции

Невозможно научиться работать с вычислительной средой без примеров, поэтому будем разбираться в MatchCAD на шаблоне.

Допустим, задана функция f(x) = (e^x/(2x-1)^2)-10 в интервале [-10;10], которую необходимо построить и провести исследование. Прежде чем приступить к построению графика функции, необходимо данную функцию перевести в математический вид в самой программе.

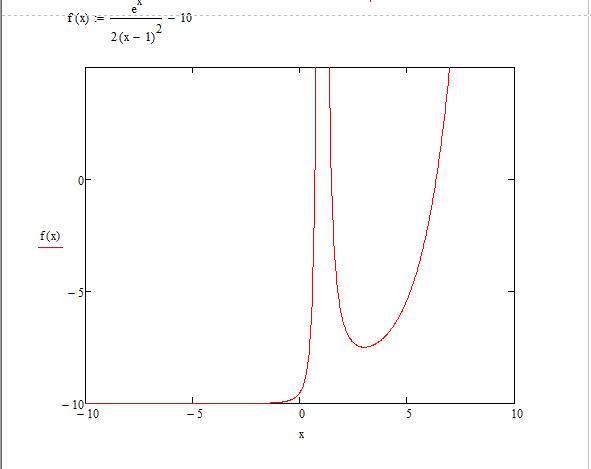
1. После того как функция была задана, следует вызвать окно быстрого графика клавишей Shift + 2. Появляется окошечко, в котором расположены 3 черных квадратика по вертикали и горизонтали.
2. По вертикали: самый верхний и нижний отвечают за интервалы значений, которые можно регулировать, средний задает функцию, по которой пользователь может построить график в "Маткаде". Крайние черные квадратики оставляем без изменения (значения автоматически присвоятся после построения), а в средний пишем нашу функцию.
3. По горизонтали: крайние отвечают за интервалы аргумента, а в средний нужно вписать "х".
4. После проделанных шагов нарисуется график функции.

Построение графика по точкам в "Маткаде"

Иногда тяжело задать функцию или посчитать ее значение, поэтому для ее построения используют метод диапазонов. В техническом задании может быть дан только диапазон значений, по которому необходимо воспроизвести изображение.

1. Зададим диапазон значений для аргумента, в рассматриваемом случае x:=-10,-8.5.. 10 (символ ".." ставится при нажатии на клавишу ";").
2. Для удобства можем отобразить получившиеся значения "х" и "у". Для первого случая используем математическую формулировку "х=", а для второго - "f(x)". Наблюдаем два столбика с соответствующими значениями.
3. Построим график, используя сочетание клавиш Shift + 2.

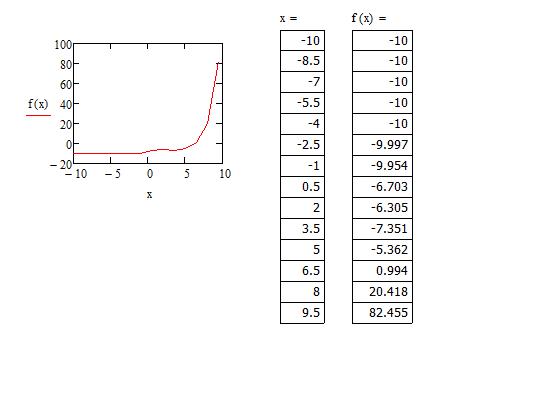
Заметим, что та часть графика, которая устремлялась вверх, исчезла, а на месте нее образовалась непрерывная функция. Все дело в том, что в первом построении функция претерпевала разрыв в некой точке. Второй график был построен по точкам, но, очевидно, что точка, которая не принадлежала графику, не отображена здесь - это одно из особенностей построения графиков по принципу точек.

Табуляция графика

Чтобы избавится от ситуации, где функция претерпевает разрыв, необходимо протабулировать график в "Маткаде" и его значения.

1. Возьмем известный нам интервал от -10 до 10.
2. Теперь запишем команду для переменного диапазона - x:=a,a + 1 .. b (не стоит забывать, что двоеточие - результат нажатия клавиши ";").
3. Смотря на заданную функцию, можно сделать вывод о том, что при значении "х=1" будет происходить деление на ноль. Чтобы без проблем протабулировать функцию, стоит исключить эту операцию так, как показано на картинке.
4. Теперь можно наглядно отобразить значения в столбиках, как мы это делали с построением по точкам. Табуляция выполнена, теперь все значения с шагом в одну единицу соответствуют своим аргументам. Обратите внимание, что на "х=1" значение аргумента не определенно.

Минимум и максимум функции

Чтобы найти минимум и максимум функции на выбранном участке графика в "Маткаде", следует использовать вспомогательный блок Given. Применяя этот блок, необходимо задать интервал поиска и начальные значения.

1. В рассматриваемом случае начальное значение x:=9.
2. Запишем рабочую команду для поиска максимального значения - X_max=Maximize(f,x) и вычисляем значение через знак равенства.
3. Через блок Given запишем условие для x.
4. Задаем минимум функции по аналогии с максимумом.
5. Результаты получились следующими: значение минимума на графике с указанным интервалом f(x) = 2,448*10¹⁹⁸, а значение минимума f(x) = -10.