Математическая программа MathCAD применяется при сложных алгебраических расчетах в то время, когда они затруднены или невозможны вручную. Данный ресурс значительно облегчает жизнь многим техническим, экономическим специальностям и студентам. Очень просто смоделировать какую-то задачу в математическом виде и получить желаемый ответ. Однако интерфейс может быть непонятен для новичков, и им тяжело адекватно воспринимать эту вычислительную среду. Одним из камней преткновения становится то, как решать систему уравнений в "Маткаде". Это очень важная функция, которую нужно изучить всем, кто желает продолжать работать в этой программе.
Как в "Маткаде" решить систему уравнений
На самом деле это не является простейшей задачей, но на рассмотренных примерах можно научиться их решать. Очень часто пользователи сталкиваются с системами уравнений и понятием "параметр". В математической рабочей среде параметр и то, как решать систему уравнений в "Маткаде", находится с помощью вспомогательной функции root. Помимо того, что нам придется привлекать эту функцию в решение, нам также понадобится значение начального приближения. Вообще, видов систем уравнений несколько, поэтому рассматривать будем конкретно на разных типах. Обсудим, с какими проблемами может столкнутся пользователь при применении функции root.
- Уравнение в изначальном виде не имеет корней.
- Корни уравнения находятся на достаточно далеком расстоянии от начального приближения.
- Уравнение претерпевает разрыв между начальным приближением и корнями.
- Уравнение имеет максимум и минимум между начальным приближением и корнями.
- Уравнение имеет комплексный корень при условии, что начальное приближение было вещественным.
Сложная функция и ее график
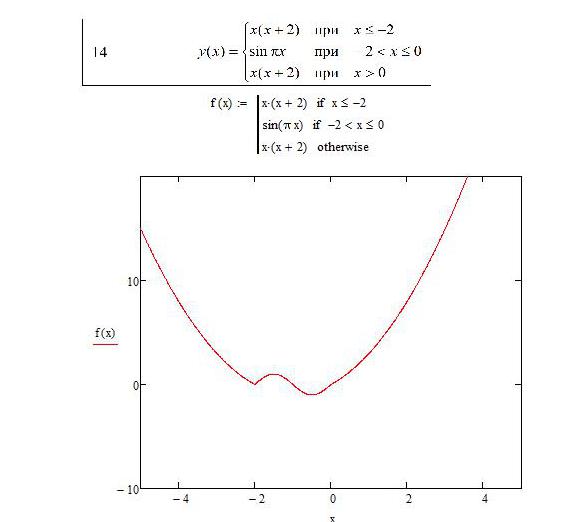
Начнем с самого простой и слегка отдаленной темы, чтобы постепенно ввести в курс дела начинающих пользователей. Это необходимо для того, чтобы символьно решить системы уравнений "Маткад", но сначала попробуем построить график для сложной функции. Пользователю нужно привести формулировку в математический вид, чтобы график функции построился корректно - так как мы имеем три участка, есть смысл воспользоваться программной конструкцией. Чтобы осуществить правильную запись уравнения, воспользуемся блоком if-otherwise.
Чтобы решить систему линейных уравнений в "Маткаде", можно использовать некоторые другие варианты. Первый способ заключается в том, что мы пишем нашу систему уравнений через оператор if. Во втором методе необходимо прибегнуть к методу логических множителей.

Строим быстрый график, нажав на сочетание клавиш Shift + 2. В появившемся окне графика вписываем функцию в средний вертикальный блок и в нижний вертикальный блок - аргумент "х".
Система нелинейных уравнений
Для нелинейных уравнение порядок нахождения корней мало чем отличается от другого типа. Допустим, имеем функцию f(x) = (e^x/(2(x-1)^2)-10 в интервале от -10 до 10 включительно. Перед тем, как решить систему нелинейных уравнений в "Маткаде", нужно построить график, чтобы оценить нули и воспользоваться табуляцией.
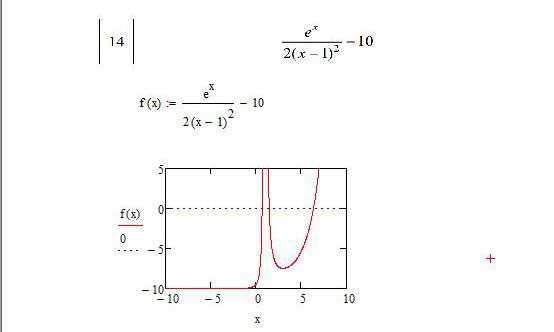
- Задаем данную функцию в математическом виде, который сможет обработать вычислительная среда.
- Строим график функции клавишами Shift + 2, обозначив функцию в вертикальном среднем окошке. В горизонтальном устанавливаем границы, как и на интервале: от -10 до 10, - и вписываем аргумент "х" в среднюю ячейку.
- Теперь нам необходимо визуально обозначить нули на графике. Сделать это можно, добавив функцию 0 (вводится в среднюю вертикальную ячейку с помощью символа ","). Стало визуально понятнее, где находятся нули функции.
- Время провести табуляцию на график, но при этом нужно задать диапазон значений. В рассматриваемом случае будем иметь x:=-1, 0.5 .. 7 (знак двоеточия ставится при помощи клавиши ";". Теперь отследим смену знака, оценив значения f(x).
Поиск корней при помощи функции root
Перед тем, как решать систему уравнений в "Маткаде", необходимо провести операцию root. Предварительно необходимо было построить функцию и протабулировать ее. После всех операций можно приступать к поиску корней с заданным интервалом. Итак, будем на примере нелинейного уравнения отвечать на вопрос, как в "Маткаде" решать систему уравнений:
- Необходимо отыскать первый корень функции "root". Присваиваем "х" следующую команду: x1:=root(f(x),x,-10,10). Затем выводим значение аргумента "х" и функции f(x1).
- Отыскиваем второй корень с помощью той же функции. Единственным отличием станет то, что поиск корня будет проходить через задание начального приближения. Возьмем начальное приближение "х:=0", чтобы применить root без интервала. Задаем функцию: x2=root(f(x),x), а следом отыскиваем значение аргумента и ее функции так же, как и в предыдущем примере.
Поиск корней функцией find
В отличие от предыдущей функции, здесь не используется задание интервала или начального приближения. Данная команда работает от того, что присваивается начальное условие - около корня. Разберем работу этой функции на том же примере:
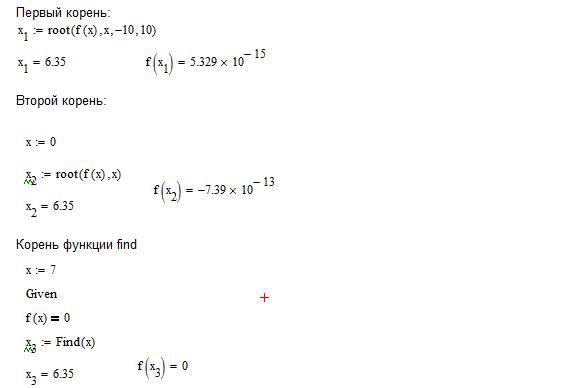
- Необходимо обозначить начальное условие: x:=7.
- Применяем кейс Given для нашей функции и присваиваем "толстое равно" на f(x)=0.
- Теперь используем саму функцию: x3 :=find(x).
- Производим поиск значения аргумента и его функции.


























