Прямая является основным геометрическим объектом на плоскости и в трехмерном пространстве. Именно из прямых строятся многие фигуры, например: параллелограмм, треугольник, призма, пирамида и так далее. Рассмотрим в статье различные способы задавания уравнений прямых.
Определение прямой и виды уравнений для ее описания
Каждый школьник хорошо себе представляет, о каком геометрическом объекте идет речь. Прямую можно представить как совокупность точек, причем если соединить каждую из них по очереди со всеми остальными, то мы получим набор параллельных векторов. Иными словами, попасть в каждую точку прямой можно из одной фиксированной ее точки, перенося ее на некоторый единичный вектор, умноженный на действительное число. Это определение прямой используется для задавания векторного равенства для ее математического описания как на плоскости, так и в трехмерном пространстве.
Прямая может быть математически представлена следующими видами уравнений:
- общее;
- векторное;
- параметрическое;
- в отрезках;
- симметричное (каноническое).
Далее рассмотрим все названные виды и покажем на примерах решения задач, как с ними работать.
Векторное и параметрическое описание прямой
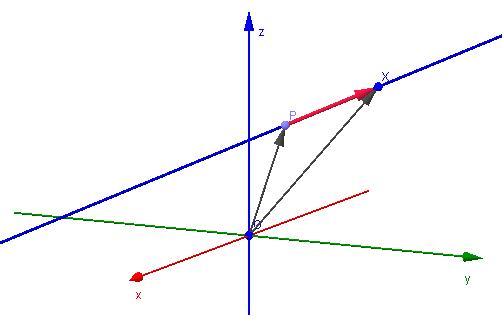
Начнем с задавания прямой через известный вектор. Предположим, что в пространстве имеется фиксированная точка M(x0; y0; z0). Известно, что прямая проходит через нее и направлена вдоль векторного отрезка v¯(a; b; c). Как по этим данным найти произвольную точку прямой? Ответ на этот вопрос даст следующее равенство:
(x; y; z) = (x0; y0; z0) + λ * (a; b; c)
Где λ - произвольное число.
Аналогичное выражение можно записать для двумерного случая, где координаты векторов и точек представлены набором из двух чисел:
(x; y) = (x0; y0) + λ * (a; b)
Записанные уравнения называются векторными, а сам направленный отрезок v¯ - это направляющий вектор для прямой.
Из записанных выражений соответствующие параметрические уравнения получаются просто, достаточно лишь переписать их в явном виде. Например, для случая в пространстве получаем следующее уравнение:
x = x0 + λ * a;
y = y0 + λ * b;
z = z0 + λ * c
С параметрическими уравнениями удобно работать, если необходимо проанализировать поведение каждой координаты. Заметим, что хотя параметр λ может принимать произвольные значения, но во всех трех равенствах он должен быть одинаковым.
Общее уравнение
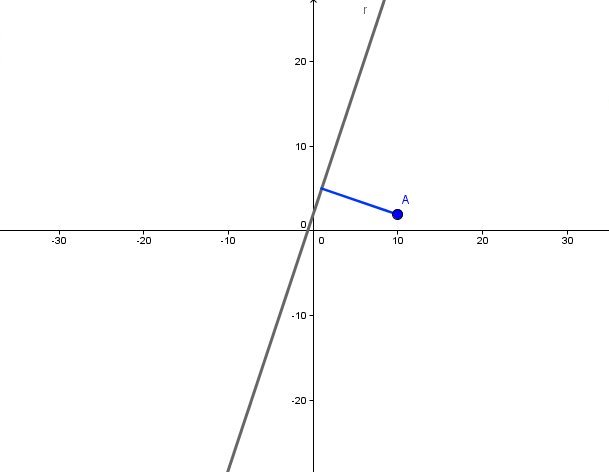
Другим способом задавания прямой, который часто используют для работы с рассматриваемым геометрическим объектом, является применение уравнения общего вида. Для двумерного случая оно имеет вид:
A * x + B * y + C = 0
Здесь большие латинские буквы представляют конкретные числовые значения. Удобство данного равенства при решении задач заключается в том, что оно в явном виде содержит вектор, который перпендикулярен прямой. Если обозначить его n¯, тогда можно записать:
n¯ = [A; B]
Кроме того, выражение удобно применять для определения расстояния от прямой до некоторой точки P(x1; y1). Формула для расстояния d имеет вид:
d = |A * x1 + B * y1 + C| / √(A2 + B2)
Несложно показать, что если из общего уравнения выразить явно переменную y, то получится следующая известная форма записи прямой:
y = k * x + b
Где k и b однозначно определяются числами A, B, C.
Уравнение в отрезках и каноническое
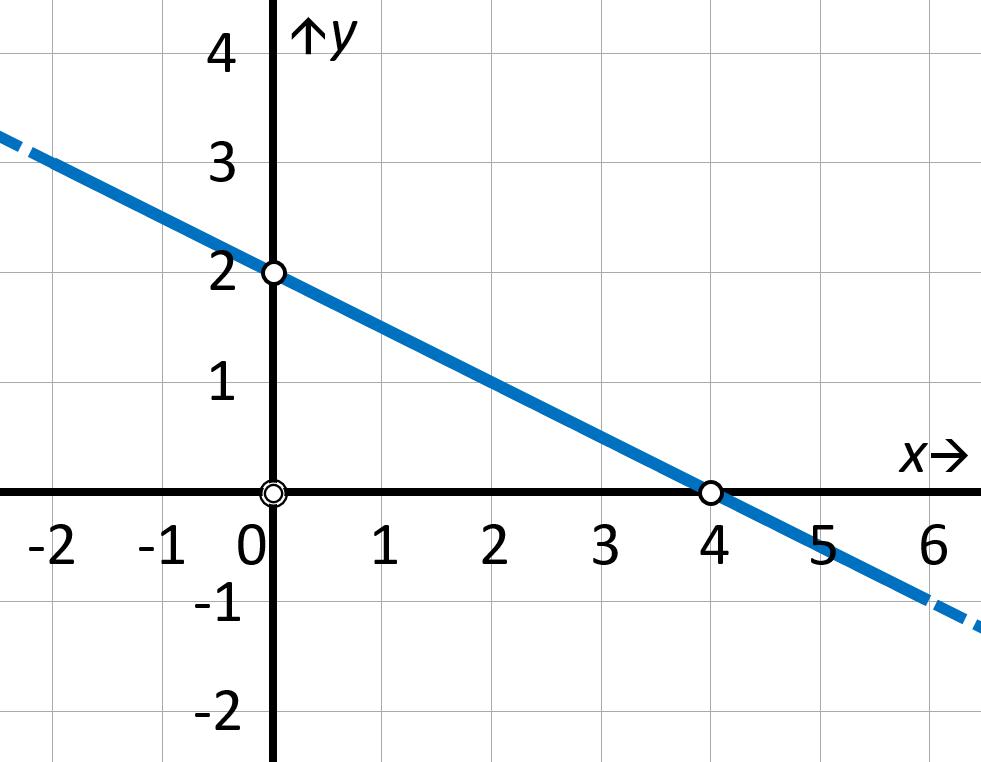
Уравнение в отрезках проще всего получить из общего вида. Покажем, как это можно сделать.
Предположим, что имеется следующая прямая:
A * x + B * y + C = 0
Перенесем свободный член в правую часть равенства, затем поделим на него все уравнение, получаем:
A * x + B * y = -C;
x / (-C / A) + y / (-C / B) = 1;
x / q + y / p = 1, где q = -C / A, p = -C / B
Мы получили так называемое уравнение в отрезках. Свое название оно получило по причине того, что знаменатель, на который делится каждая переменная, показывает значение координаты пересечения прямой с соответствующей осью. Этот факт удобно использовать для изображения прямой в координатной системе, а также для анализа ее взаимного расположения по отношению к другим геометрическим объектам (прямым, точкам).
Теперь перейдем к получению канонического уравнения. Это проще сделать, если рассмотреть параметрический вариант. Для случая на плоскости имеем:
x = x0 + λ * a;
y = y0 + λ * b
Выразим параметр λ в каждом равенстве, затем приравняем их, получаем:
λ = (x - x0) / a;
λ = (y - y0) / b;
(x - x0) / a = (y - y0) / b
Это и есть искомое уравнение, записанное в симметричной форме. Так же, как и векторное выражение, оно в явной форме содержит координаты направляющего вектора и координаты одной из точек, которая принадлежит прямой.
Можно заметить, что в данном пункте мы привели уравнения для двумерного случая. Аналогичным образом можно составить уравнение прямой в пространстве. Здесь нужно заметить, что если каноническая форма записи и выражение в отрезках будут иметь такой же вид, то общее уравнение в пространстве для прямой представляется системой из двух уравнений для пересекающихся плоскостей.
Задача на построение уравнения прямой
Из геометрии каждый школьник знает, что через две точки можно начертить единственную линию. Предположим, что в координатной плоскости заданы следующие точки:
M1(1; 2);
M2(-1; 3)
Следует найти уравнение прямой, которой принадлежат обе точки, в отрезках, в векторном, каноническом и в общем виде.
Получим сначала векторное уравнение. Для этого следует определить для прямой направляющий вектор M1M2¯:
M1M2¯ = (-1; 3) - (1; 2) = (-2; 1)
Теперь можно составить векторное уравнение, взяв одну из двух заданных в условии задачи точек, например, M2:
(x; y) = (-1; 3) + λ * (-2; 1)
Чтобы получить каноническое уравнение, достаточно преобразовать найденное равенство в параметрический вид и исключить параметр λ. Имеем:
x = -1 - 2 * λ, следовательно, λ = x + 1 / (-2);
y = 3 + λ, далее получаем λ = y - 3;
x + 1 / (-2) = (y - 3) / 1
Оставшиеся два уравнения (общее и в отрезках) можно найти из канонического, преобразуя его следующим образом:
x + 1 = -2 * y + 6;
общее уравнение: x + 2 * y - 5 = 0;
в отрезках уравнение: x / 5 + y / 2,5 = 1
Полученные уравнения показывают, что вектор (1; 2) должен быть перпендикулярен прямой. Действительно, если найти его скалярное произведение с направляющим вектором, то оно будет равно нулю. Уравнение в отрезках говорит, что прямая пересекает ось x в точке (5; 0), а ось y - в точке (2,5; 0).
Задача на определение точки пересечения прямых
На плоскости заданы две прямые следующими уравнениями:
2 * x + y -1 = 0;
(x; y) = (0; -1) + λ * (-1; 3)
Необходимо определить координаты точки, в которой эти прямые пересекаются.
Решить задачу можно двумя способами:
- Преобразовать векторное уравнение в общий вид, затем решить систему из двух линейных уравнений.
- Не выполнять никаких преобразований, а просто подставить координату точки пересечения, выраженную через параметр λ, в первое уравнение. Затем найти значение параметра.
Поступим вторым способом. Имеем:
x = -λ;
y = -1 + 3 * λ;
2 * (-λ) + (-1) + 3 * λ - 1 = 0;
λ = 2
Подставляем полученное число в векторное уравнение:
(x; y) = (0; -1) + 2 * (-1; 3) = (-2; 5)
Таким образом, единственной точкой, которая принадлежит обеим прямым, является точка с координатами (-2; 5). В ней прямые пересекаются.


























