Точки приложения сил трения покоя, скольжения и качения. Пример задачи

Каждому школьнику известно, что при наличии контакта между двумя твердыми поверхностями возникает так называемая сила трения. Рассмотрим в данной статье, что она собой представляет, концентрируя свое внимание на точке приложения силы трения.

Каких видов бывает сила трения?

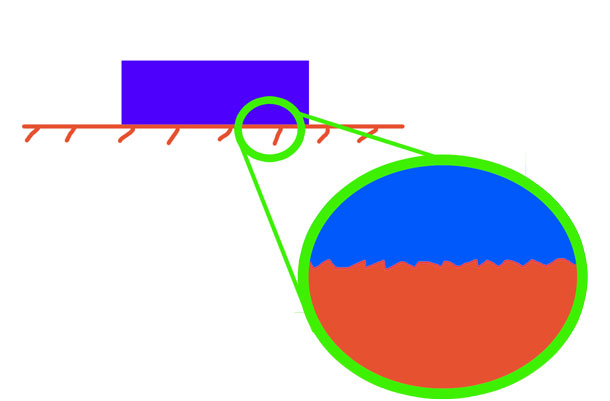
Прежде чем рассматривать точку приложения силы трения, необходимо кратко вспомнить, какие виды трения существуют в природе и технике.

Начнем рассматривать трение покоя. Этот вид характеризует состояние покоящегося твердого тела на какой-нибудь поверхности. Трение покоя препятствует любому смещению тела из его состояния покоя. Например, по причине действия этой самой силы нам трудно сдвинуть шкаф, стоящий на полу.

Трение скольжения — это еще один вид трения. Проявляет он себя в случае контакта между двумя скользящими друг по другу поверхностями. Трение скольжения препятствует движению (направление трения силы противоположно скорости тела). Ярким примером его действия является скольжение по снегу лыжника или конькобежца по льду.

Наконец, третий вид трения — это качение. Он существует всегда, когда одно тело катится по поверхности другого. Например, качение колеса или подшипников — это яркие примеры, когда важно учитывать силу трения качения.

Первые два из описанных видов возникают из-за шероховатостей на трущихся поверхностях. Третий же вид возникает по причине деформационного гистерезиса катящегося тела.

Точки приложения сил трения скольжения и покоя

Выше было сказано, что трение покоя препятствует внешней действующей силе, которая стремится сдвинуть с места объект вдоль поверхности контакта. Это означает, что направление силы трения противоположно направлению параллельной к поверхности внешней силы. Точка приложения рассматриваемой силы трения находится в области контакта двух поверхностей.

Важно понимать, что сила трения покоя не является величиной постоянной. Она имеет максимальное значение, которое рассчитывается по следующей формуле:

F_t = µ_t*N.

Однако это максимальное значение появляется только тогда, когда тело начинает свое движение. В любом другом случае сила трения покоя по модулю точно равна параллельной поверхности внешней силы.

Что касается точки приложения силы трения скольжения, то она не отличается от таковой для трения покоя. Говоря о разнице между трением покоя и скольжения, следует отметить абсолютное значение этих сил. Так, сила трения скольжения для данной пары материалов является постоянной величиной. Кроме того, она всегда меньше максимальной силы трения покоя.

Как можно заметить, точка приложения сил трения не совпадает с центром тяжести тела. Это означает, что рассматриваемые силы создают момент, стремящийся опрокинуть скользящее тело вперед. Последнее можно наблюдать, когда велосипедист резко тормозит передним колесом.

Трение качения и ее точка приложения

Поскольку физическая причина появления трения качения отличается от таковой для рассмотренных выше видов трения, то точка приложения силы трения качения имеет несколько иной характер.

Предположим, что колесо автомобиля стоит на асфальте. Очевидно, что это колесо деформируется. Площадь соприкосновения его с асфальтом равна 2*d*l, где l - ширина колеса, 2*d - длина бокового контакта колеса и асфальта. Сила трения качения по своей физической сути проявляется в виде момента реакции опоры, направленного против вращения колеса. Этот момент рассчитывается так:

M = N*d

Если его разделить и умножить на радиус колеса R, тогда получим:

M = N*d/R*R = F_t*R, где F_t = N*d/R

Таким образом, сила трения качения F_t в действительности является реакцией опоры, создающей момент силы, который стремится замедлить вращение колеса.

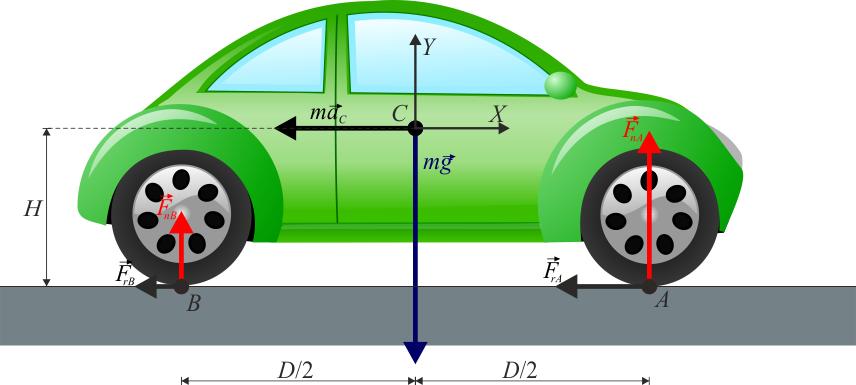
Точка приложения этой силы направлена вертикально вверх относительно поверхности плоскости и смещена вправо от центра масс на величину d (при условии, что колесо движется слева направо).

Пример решения задачи

Действие трения силы любого вида стремится замедлить механическое движение тел, переводя при этом их кинетическую энергию в тепловую. Решим следующую задачу:

• брусок скользит по наклонной поверхности. Необходимо рассчитать ускорение его движения, если известно, что коэффициент для скольжения равен 0,35, а угол наклона поверхности равен 35^o.

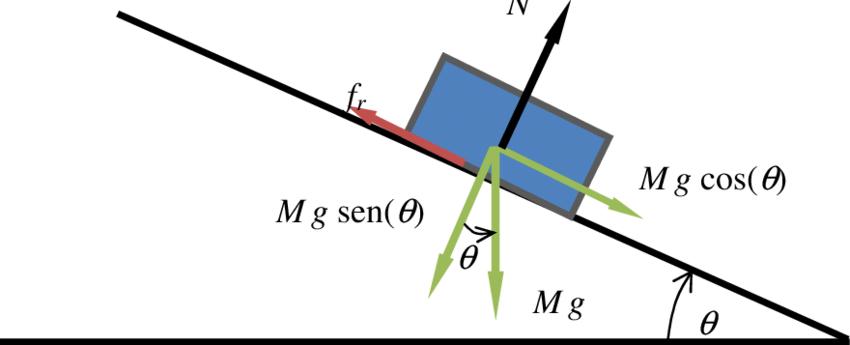
Рассмотрим, какие силы на брусок действуют. Во-первых, вниз вдоль поверхности скольжения направлена силы тяжести составляющая. Она равна:

F = m*g*sin(α)

Во-вторых, вверх вдоль по плоскости действует постоянная сила трения, которая направлена против вектора ускорения тела. Ее можно определить по формуле:

F_t = µ_t*N = µ_t*m*g*cos(α)

Тогда закон Ньютона для движущегося с ускорением a бруска примет вид:

m*a = m*g*sin(α) - µ_t*m*g*cos(α) =>

a = g*sin(α) - µ_t*g*cos(α)

Подставляя в равенство данные, получаем, что a = 2,81 м/с². Заметим, что найденное ускорение не зависит от массы бруска.