Одним из характерных свойств любой волны является ее способность дифрагировать на препятствиях, размер которых сравним с длиной этой волны. Отмеченное свойство используют в так называемых дифракционных решетках. Что это такое, и как их можно применять для анализа спектров излучения и поглощения разных материалов, рассматривается в статье.
Явление дифракции
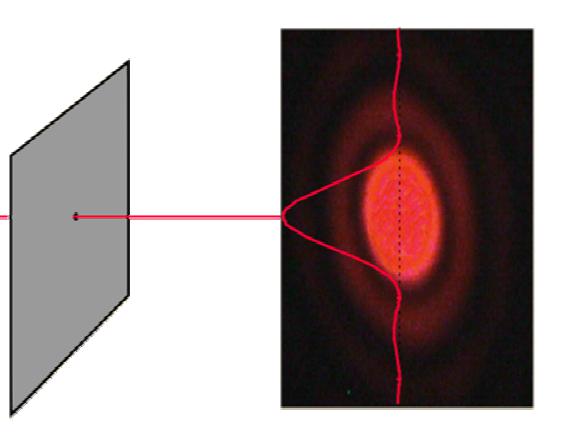
Это явление заключается в изменении траектории прямолинейного распространения волны, когда на ее пути появляется препятствие. В отличие от преломления и отражения, дифракция заметна только на очень маленьких препятствиях, геометрические размеры которых – порядка длины волны. Выделяют дифракцию двух видов:
- огибание волной объекта, когда длина волны намного больше размеров этого объекта;
- рассеяние волны при прохождении через отверстия разной геометрической формы, когда размеры отверстий оказываются меньше, чем длина волны.
Явление дифракции характерно для звуковых, морских и электромагнитных волн. Далее в статье будем рассматривать дифракционную решетку только для света.
Явление интерференции
Дифракционные картины, возникающие на разных препятствиях (круглых отверстиях, щелях и решетках), являются результатом не только дифракции, но и интерференции. Суть последней заключается в наложении волн друг на друга, которые испускаются разными источниками. Если эти источники излучают волны, сохраняя между ними разность фаз (свойство когерентности), тогда можно наблюдать во времени устойчивую интерференционную картину.
Положение максимумов (яркие области) и минимумов (темные зоны) объясняется следующим образом: если две волны приходят в данную точку в противофазе (одна с максимальной, а другая с минимальной абсолютной амплитудой), то они "уничтожают" друг друга, и в точке наблюдается минимум. Наоборот, если две волны приходят в одинаковой фазе в точку, то они будут усиливать друг друга (максимум).
Оба явление впервые описал англичанин Томас Юнг в 1801 году, когда исследовал дифракцию на двух щелях. Однако, наблюдал впервые это явление итальянец Гримальди в 1648 году, когда исследовал дифракционную картину, даваемую солнечным светом, проходящим через маленькое отверстие. Гримальди не смог объяснить результаты своих экспериментов.
Математический метод, используемый для изучения дифракции

Этот метод называется принципом Гюйгенса-Френеля. Заключается он в утверждении, что в процессе распространения волнового фронта каждая его точка является источником вторичных волн, интерференция которых определяет результирующее колебание в произвольной рассматриваемой точке.
Описанный принцип был развит Огюстеном Френелем в первой половине XIX века. При этом Френель исходил из идей волновой теории Христиана Гюйгенса.
Хотя принцип Гюйгенса-Френеля не является теоретически строгим, он с успехом используется для математического описания экспериментов с дифракцией и интерференцией.
Дифракция в ближнем и дальнем полях
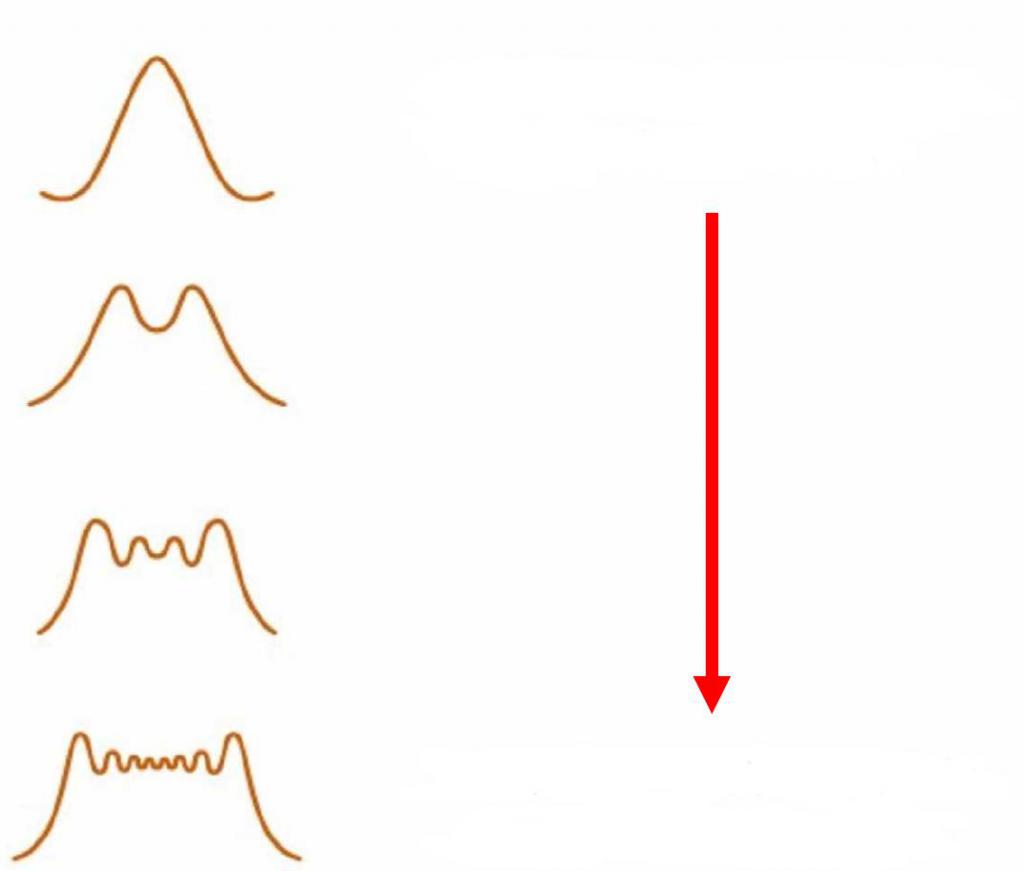
Дифракция - это достаточно сложное явление, точное математическое решение для которого требует рассмотрения теории электромагнетизма Максвелла. Поэтому на практике рассматривают лишь частные случаи этого явления, используя различные приближения. Если волновой фронт, падающий на препятствие, является плоским, тогда различают два вида дифракции:
- в ближнем поле, или дифракция Френеля;
- в дальнем поле, или дифракция Фраунгофера.
Под словами "дальнее и ближнее поле" имеется в виду расстояние до экрана, на котором наблюдают дифракционную картину.
Переход между дифракциями Фраунгофера и Френеля можно оценить, если вычислить число Френеля для конкретного случая. Это число определяется так:
F = a2/(D*λ).
Здесь λ - длина волны света, D - дистанция до экрана, a - размер объекта, на котором происходит дифракция.
Если F<<1 (например, 0,001), тогда речь идет о дифракции Фраунгофера, если F>1, тогда следует рассматривать уже приближения ближнего поля.
Многие практические случаи, в том числе и использование дифракционной решетки, рассматриваются в приближении дальнего поля.
Понятие о решетке, на которой дифрагируют волны
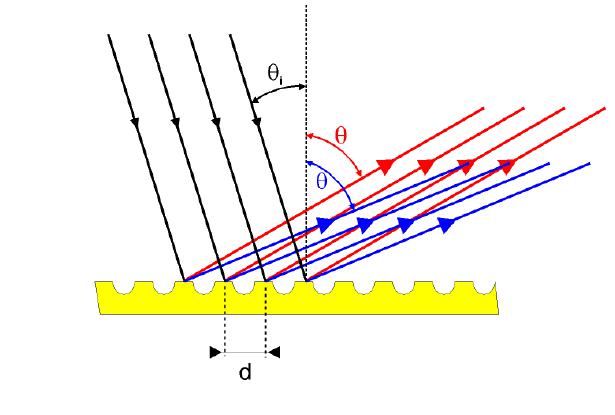
Эта решетка представляет собой небольшой плоский объект, на который каким-либо способом нанесена периодическая структура, например, полосы или бороздки. Важным параметром такой решетки является количество полос на единицу длины (обычно на 1 мм). Этот параметр называется постоянной решетки. Далее будем его обозначать символом N. Величина, обратная N, определяет расстояние между соседними полосами. Обозначим его буквой d, тогда:
d = 1/N.
Когда плоская волна падает на такую решетку, то она испытывает периодические возмущения. Последние на экране отображаются в виде некоторой картины, являющейся результатом интерференции волн.
Виды решеток
Существует два вида дифракционных решеток:
- проходящие, или прозрачные;
- отражающие.
Первые изготавливаются путем нанесения непрозрачных штрихов на стекло. Именно с такими пластинками осуществляют работу в лабораториях, они используются в спектроскопах.
Второй вид, то есть отражающие решетки, изготавливаются с помощью нанесение периодических бороздок на отполированный материал. Ярким бытовым примером такой решетки является пластиковый диск CD или DVD.

Уравнение решетки
Рассматривая дифракцию Фраунгофера на решетке, для интенсивности света на дифракционной картине можно записать следующее выражение:
I(θ) = I0*(sin(β)/β)2*[sin(N*α)/sin(α)]2, где
α = pi*d/λ*(sin(θ)-sin(θ0));
β = pi*a/λ*(sin(θ)-sin(θ0)).
Параметр a - это ширина одной щели, а параметр d - это расстояние между ними. Важной характеристикой в выражении для I(θ) является угол θ. Это угол между центральным перпендикуляром к плоскости решетки и конкретной точкой на дифракционной картине. В экспериментах его измеряют с помощью гониометра.
В представленной формуле выражение в круглых скобках определяет дифракцию от одной щели, а выражение в квадратных скобках - это результат интерференции волн. Анализируя его на условие интерференционных максимумов, можно прийти к следующей формуле:
sin(θm)-sin(θ0) = m*λ/d.
Угол θ0 характеризует падающую волну на решетку. Если фронт волны будет параллелен ей, тогда θ0 = 0, и последнее выражение приобретает форму:
sin(θm) = m*λ/d.
Эта формула называется уравнением дифракционной решетки. Величина m приобретает любые целые числа, включая отрицательные и ноль, она называется порядком дифракции.
Анализ уравнения решетки

В предыдущем пункте мы выяснили, что положение главных максимумов описывается уравнением:
sin(θm) = m*λ/d.
Как можно его применять на практике? Главным образом его используют, когда разлагают на отдельные цвета падающий на дифракционную решетку с периодом d свет. Чем больше длина волны λ, тем будет больше угловое расстояние до максимума, который ей соответствует. Измерение соответствующих θm для каждой волны позволяет рассчитать ее длину, а значит, определить весь спектр излучающего объекта. Сравнивая этот спектр с данными из известной базы, можно сказать, излучением каких химических элементов он испущен.
Описанный выше процесс применяется в спектрометрах.
Разрешающая способность решетки
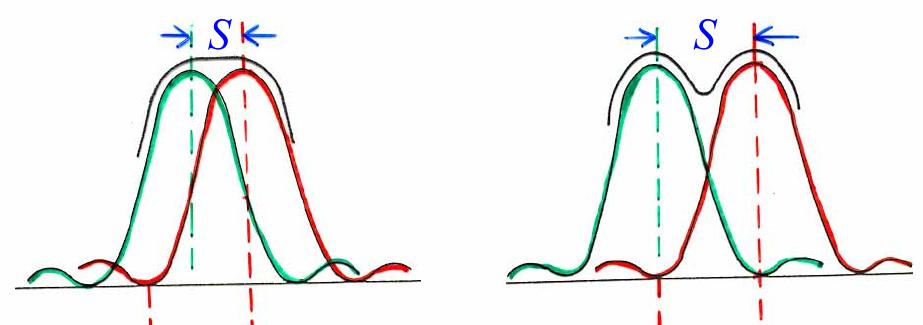
Под ней понимают такую разницу между двумя длинами волн, которые на дифракционной картине появляются в виде отдельных линий. Дело в том, что каждая линия имеет определенную толщину, когда две волны с близкими значениями λ и λ+Δλ дифрагируют, то соответствующие им линии на картине могут слиться в одну. В последнем случае говорят, что разрешающая способность решетки меньше, чем Δλ.
Опуская рассуждения касательно вывода формулы для разрешающей способности решетки, приведем ее конечный вид:
Δλ>λ/(m*N).
Это небольшая формула позволяет сделать вывод: с помощью решетки можно разделить тем более близкие длины волн (Δλ), чем больше длина волны света λ, чем больше число штрихов на единице длины (постоянная решетки N), и чем выше порядок дифракции. На последнем остановимся подробнее.
Если взглянуть на дифракционную картину, то с увеличением m действительно происходит увеличение расстояния между соседними длинами волн. Однако для использования высоких порядков дифракции необходимо, чтобы интенсивность света на них была достаточной, для проведения измерений. На обычной дифракционной решетке она быстро падает с увеличением m. Поэтому для этих целей используют специальные решетки, которые изготавливают таким образом, чтобы перераспределить интенсивность света в пользу больших m. Как правило, это отражающие решетки, дифракционная картина на которых получается для больших θ0.
Далее рассмотрим использование уравнения решетки для решения нескольких задач.
Задачи, на определение углов дифракции, порядка дифракции и постоянной решетки
Приведем примеры решения нескольких задач:
- Для определения периода дифракционной решетки проводят следующий эксперимент: берут монохроматический источник света, длина волны которого является известной величиной. С помощью линз формируют параллельный фронт волны, то есть создают условия для дифракции Фраунгофера. Затем этот фронт направляют на дифракционную решетку, период которой неизвестен. На получившейся картине измеряют с помощью гониометра углы для разных порядков. Потом по формуле вычисляют значение неизвестного периода. Проведем этот расчет на конкретном примере.
Пусть длина волны света равна 500 нм, а угол для первого порядка дифракции составляет 21o. По этим данным необходимо определить период дифракционной решетки d.
Используя уравнение решетки, выражаем d и подставляем данные:
d = m*λ/sin(θm) = 1*500*10-9/sin(21o) ≈ 1,4 мкм.
Тогда постоянная решетки N равна:
N = 1/d ≈ 714 штрихов на 1 мм.
- Свет нормально падает на дифракционную решетку, имеющую период 5 мкм. Зная, что длина волны λ = 600 нм, необходимо найти углы, под которыми появятся максимумы первого и второго порядков.
Для первого максимума получаем:
sin(θ1) = λ/d => θ1 = arcsin(λ/d) ≈ 6,9o.
Второй максимум появится для угла θ2:
θ2 = arcsin(2*λ/d) ≈ 13,9o.
- На дифракционную решетку с периодом 2 мкм падает монохроматический свет. Длина его волны равна 550 нм. Необходимо найти, сколько дифракционных порядков появится на полученной картине на экране.
Такой тип задач решается так: сначала следует определить зависимость угла θm от порядка дифракции для условий задачи. После этого необходимо будет учесть, что функция синус не может принимать значения больше, чем единица. Последний факт позволит получить ответ на эту задачу. Проделаем описанные действия:
sin(θm) = m*λ/d = 0,275*m.
Это равенство показывает, что при величине m = 4 выражение в правой части станет равным 1,1, а при m = 3 будет равно 0,825. Это означает, что при помощи дифракционной решетки с периодом 2 мкм на длине волны 550 нм можно получить максимально 3-й порядок дифракции.
Задача на вычисление разрешающей способности решетки
Предположим, что для опыта собираются использовать дифракционную решетку с периодом 10 мкм. Необходимо рассчитать, на какую минимальную длину могут отличаться волны вблизи λ = 580 нм, чтобы они появлялись в виде отдельных максимумов на экране.
Ответ на эту задачу связан с определением разрешающей способности рассматриваемой решетки для заданной длины волны. Итак, две волны могут отличаться на Δλ>λ/(m*N). Поскольку постоянная решетки обратно пропорциональна периоду d, то это выражение можно записать так:
Δλ>λ*d/m.
Теперь для длины волны λ = 580 нм запишем уравнение решетки:
sin(θm) = m*λ/d = 0,058*m.
Откуда получаем, что максимальный порядок m будет равен 17. Подставляя это число в формулу для Δλ, имеем:
Δλ>580*10-9*10*10-6/17 = 3,4*10-13 или 0,00034 нм.
Мы получили очень большую разрешающую способность, когда период дифракционной решетки равен 10 мкм. На практике, как правило, она не достигается ввиду низких интенсивностей максимумов высоких порядков дифракции.



























