Вращение вокруг оси или точки различных объектов является одним из важных видов движения в технике и в природе, который изучают в курсе физики. Динамика вращения, в отличие от динамики линейного движения, оперирует понятием момента той или иной физической величины. Данная статья посвящена вопросу, что такое момент сил.
Понятие о моменте силы
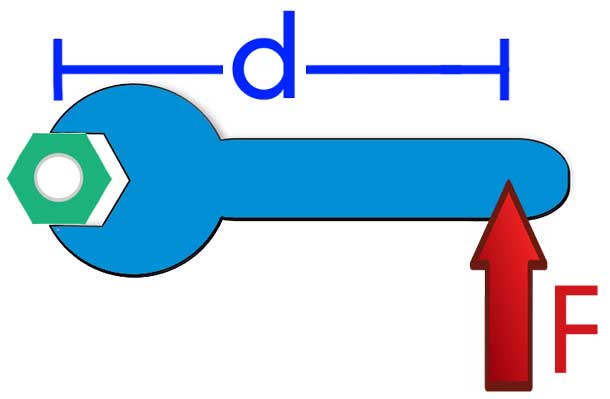
Каждый любитель велосипеда хотя бы один раз в своей жизни раскручивал рукой колесо своего "железного коня". Если описанное действие выполнять, взявшись рукой за покрышку, то раскрутить колесо гораздо легче, чем взявшись за спицы ближе к оси вращения. Это простое действие описывается в физике с помощью момента силы или вращающего момента.
Что такое момент силы? Ответить на этот вопрос можно, если представить себе систему, которая может вращаться вокруг оси O. Если в некоторой точке P к системе приложить вектор силы F¯, тогда момент действующей силы F¯ будет равен:
M¯ = [OP¯*F¯].
То есть момент M¯ представляет собой векторную величину, равную произведению векторной силы F¯ на радиус-вектор OP¯.
Записанная формула позволяет отметить важный факт: если внешняя сила F¯ приложена под любым углом к любой точке оси вращения, то момента она не создает.
Абсолютная величина момента силы
В предыдущем пункте мы рассмотрели определение, что такое момент силы относительно оси. Теперь обратимся к рисунку ниже.
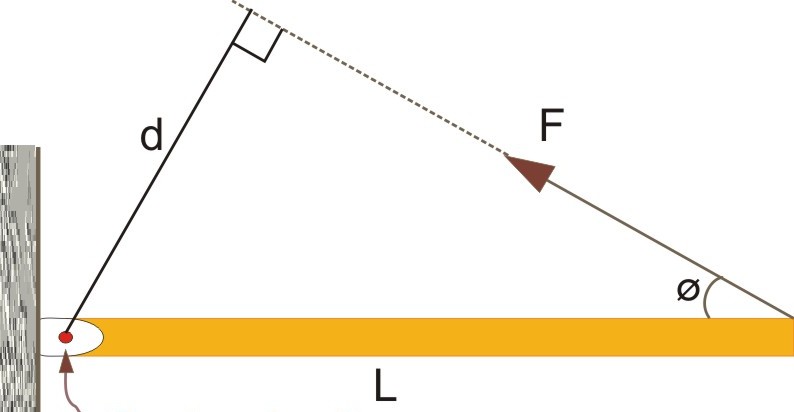
Здесь изображен некоторый стержень, имеющий длину L. С одной стороны он закреплен через шарнирное соединение на вертикальной стене. Другой конец стержня является свободным. На этот конец оказывает действие сила F¯. Также известен угол между стержнем и вектором силы. Он равен φ.
Вращающий момент определяется через векторное произведение. Модуль такого произведения равен произведению абсолютных значений векторов на синус угла между ними. Применяя тригонометрические формулы, приходим к следующему равенству:
M = L*F*sin(φ).
Обращаясь снова к рисунку выше, можно это равенство переписать в следующей форме:
M = d*F, где d = L*sin(φ).
Величина d, которая равна расстоянию от вектора силы до оси вращения, получила название рычага силы. Чем больше значение d, тем больший момент создаст сила F.
Направление момента силы и его знак
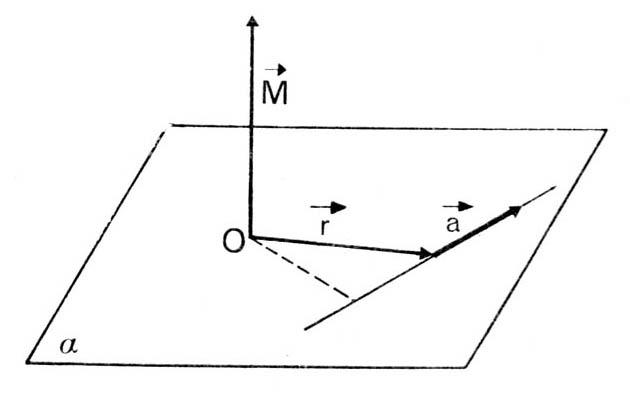
Изучение вопроса, что такое момент силы, не может быть полным, если не рассмотреть его векторную природу. Вспоминая свойства векторного произведения, можно с уверенностью сказать, что момент силы будет перпендикулярен плоскости, построенной на векторах-множителях.
Конкретное направление M¯ определяется однозначно, если применить так называемое правило буравчика. Звучит оно просто: вращая буравчик по направлению кругового движения системы, поступательным движением буравчика определяется направление момента силы.
Если смотреть на вращающуюся систему вдоль ее оси, то вектор момента силы, приложенный к точке, может быть направлен как на читателя, так и от него. В связи с этим при количественных расчетах используют понятие о положительном или об отрицательном моменте. В физике принято положительным считать тот момент силы, который приводит к вращению системы против хода часовой стрелки.
В чем смысл величины M¯?
Имеется в виду физический смысл. Действительно, в механике линейного движения известно, что сила - это мера возможности придать линейное ускорение телу. По аналогии, момент силы точки - это мера возможности сообщения углового ускорения системы. Момент силы является причиной появления углового ускорения и ему прямо пропорционален.
Разную возможность совершения вращения или поворота легко понять, если вспомнить, что дверь открывается легче, если ее толкнуть подальше от дверных петель, то есть в области ручки. Еще один пример: любой более-менее тяжелый предмет легче удержать, если прижать руку к телу, чем держать его на вытянутой руке. Наконец, открутить гайку проще, если воспользоваться длинным ключом. В названных примерах момент силы изменяется за счет уменьшения или увеличения рычага силы.

Здесь уместно привести аналогию философского характера, взяв за пример книгу Экхарта Толле "Сила момента Сейчас". Книга относится к психологическому жанру и учит жить без стресса в данный момент своей жизни. Только текущее мгновение имеет смысл, только во время него совершаются все действия. Учитывая названную идею книги "Сила момента Сейчас" можно сказать, что вращающий момент в физике осуществляет ускорение или замедление вращения в текущий момент времени. Поэтому главное уравнение моментов имеет следующий вид:
dL = M*dt.
Где dL - изменение момента импульса за бесконечно малый промежуток времени dt.
Важность понятия о моменте силы для статики

Многие знакомы с задачами на рычаги разного рода. Практически во всех этих задачах статики требуется найти условия равновесия системы. Для нахождения этих условий проще всего воспользоваться концепцией момента силы.
Если система не движется и находится в состоянии равновесия, то сумма всех моментов сил относительно оси, точки или выбранной опоры должна быть равна нулю, то есть:
∑i=1nMi¯ = 0.
Где n - число действующих сил.
Напомним, что абсолютные значения моментов Mi в равенство выше нужно подставлять с учетом их знака. Сила реакции опоры, которая рассматривается в качестве оси вращения, вращающего момента не создает. Ниже приводится видео, которое поясняет тему этого пункта статьи.

Момент силы и его работа
Многие читатели обратили внимание, что момент силы рассчитывается в ньютонах на метр. Это означает, что он имеет такую же размерность, что работа или энергия в физике. Тем не менее концепция момента силы - это величина векторная, а не скалярная, поэтому работой момент M¯ считать нельзя. Однако работу он может выполнять, что рассчитывается по такой формуле:
A = M*θ.
Где θ - центральный угол в радианах, на который система повернулась за известное время t.