Вращение является типичным видом механического движения, которое часто встречается в природе и технике. Любое вращение возникает в результате воздействия некоторой внешней силы на рассматриваемую систему. Эта сила создает так называемый вращающий момент. Что он собой представляет, от чего зависит, рассматривается в статье.
Процесс вращения
Прежде чем рассматривать концепцию вращающего момента, дадим характеристику систем, к которым может быть применена эта концепция. Система вращения предполагает наличие в ней оси, вокруг которой осуществляется круговое движение или поворот. Расстояние от этой оси до материальных точек системы называется радиусом вращения.
С точки зрения кинематики, процесс характеризуется тремя угловыми величинами:
- углом поворота θ (измеряется в радианах);
- угловой скоростью ω (измеряется в радианах в секунду);
- ускорением угловым α (измеряется в радианах в секунду квадратную).
Эти величины связаны друг с другом следующими равенствами:
ω = dθ/dt;
α = dω/dt.
Примерами вращения в природе являются движения планет по своим орбитам и вокруг своих осей, движения смерчей. В быту и технике рассматриваемое движение характерно для моторов двигателей, гаечных ключей, строительных кранов, открывания дверей и так далее.
Определение момента силы
Теперь перейдем к непосредственной теме статьи. Согласно физическому определению, момент силы представляет собой векторное произведение вектора приложения силы относительно оси вращения на вектор самой силы. Соответствующее математическое выражение можно записать так:
M¯ = [r¯*F¯].
Здесь вектор r¯ направлен от оси вращения к точке приложения силы F¯.
В этой формуле вращающего момента M¯ сила F¯ может быть направлена как угодно относительно направления оси. Тем не менее параллельная оси компонента силы не будет создавать вращения, если ось жестко закреплена. В большинстве задач по физике приходится рассматривать силы F¯, которые лежат в плоскостях перпендикулярных оси вращения. В этих случаях абсолютное значение вращающего момента можно определить по следующей формуле:
|M¯| = |r¯|*|F¯|*sin(β).
Где β является углом между векторами r¯ и F¯.
Что такое рычаг силы?
Рычаг силы играет важную роль при определении величины момента силы. Чтобы понять, о чем идет речь, рассмотрим следующий рисунок.
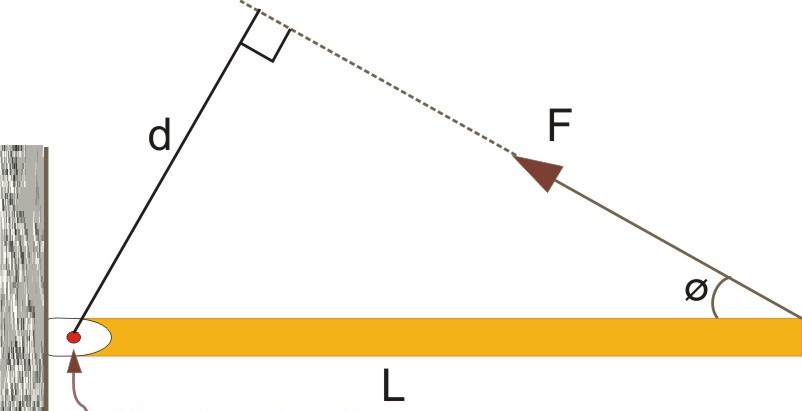
Здесь показан некоторый стержень длиною L, который закреплен в точке вращения одним из своих концов. На другой конец действует сила F, направленная под острым углом φ. Согласно определению момента силы, можно записать:
M = F*L*sin(180o-φ).
Угол (180o-φ) появился потому, что вектор L¯ направлен от закрепленного конца к свободному. Учитывая периодичность тригонометрической функции синуса, можно переписать это равенство в таком виде:
M = F*L*sin(φ).
Теперь обратим внимание на прямоугольный треугольник, построенный на сторонах L, d и F. По определению функции синуса, произведение гипотенузы L на синус угла φ дает значение катета d. Тогда приходим к равенству:
M = F*d.
Линейная величина d называется рычагом силы. Он равен расстоянию от вектора силы F¯ до оси вращения. Как видно из формулы, понятием рычага силы удобно пользоваться при вычислении момента M. Полученная формула говорит о том, что вращающий момент максимальный для некоторой силы F будет возникать только тогда, когда длина радиус-вектора r¯ (L¯ на рисунке выше) будет равна рычагу силы, то есть r¯ и F¯ будут взаимно перпендикулярны.
Направление действия величины M¯
Выше было показано, что вращающий момент - это векторная характеристика для данной системы. Куда направлен этот вектор? Ответить на этот вопрос не представляет особого труда, если вспомнить, что результатом произведения двух векторов является третий вектор, который лежит на оси, перпендикулярной плоскости расположения исходных векторов.
Остается решить, будет ли направлен момент силы вверх или вниз (на читателя или от него) относительно упомянутой плоскости. Определить это можно или по правилу буравчика, или с помощью правила правой руки. Приведем оба правила:
- Правило правой руки. Если расположить правую кисть таким образом, чтобы четыре ее пальца двигались от начала вектора r¯ к его концу, а затем от начала вектора F¯ к его концу, то большой палец, оттопыренный, укажет на направление момента M¯.
- Правило буравчика. Если направление вращения воображаемого буравчика совпадает с направлением вращательного движения системы, то поступательное движение буравчика укажет на направление вектора M¯. Напомним, что он вращается только по часовой стрелке.
Оба правила являются равноправными, поэтому каждый может использовать то, которое является для него более удобным.
При решении практических задач разное направление вращающего момента (вверх - вниз, влево - вправо) учитывается с помощью знаков "+" или "-". Следует запомнить, что за положительное направление момента M¯ принято считать такое, которое приводит к вращению системы против часовой стрелки. Соответственно, если некоторая сила приводит к вращению системы по ходу стрелки часов, то создаваемый ее момент будет иметь отрицательную величину.
Физический смысл величины M¯
В физике и механике вращения величина M¯ определяет способность силы или суммы сил совершать вращение. Поскольку в математическом определении величины M¯ стоит не только сила, но и радиус-вектор ее приложения, то именно последний во многом определяет отмеченную вращательную способность. Чтобы понятнее было, о какой способности идет речь, приведем несколько примеров:
- Каждый человек, хотя бы один раз в жизни пытался открыть дверь, взявшись не за ручку, а толкнув ее недалеко от петель. В последнем случае приходится прилагать значительное усилие, чтобы добиться желаемого результата.
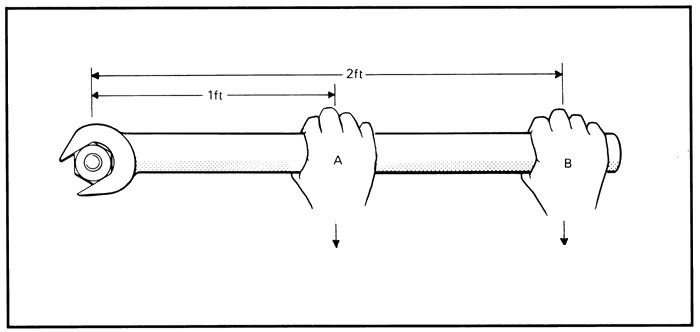
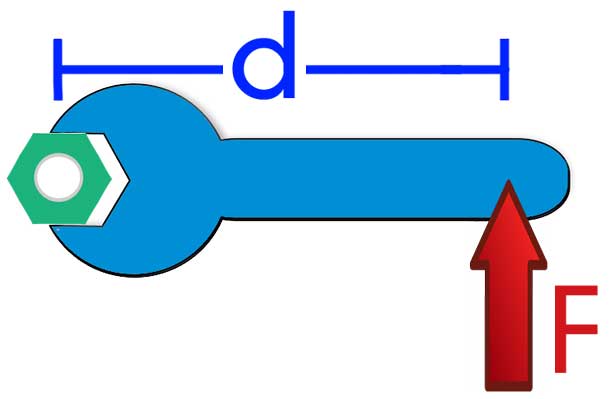
- Чтобы открутить гайку с болта, используют специальные гаечные ключи. Чем длиннее ключ, тем легче открутить гайку.
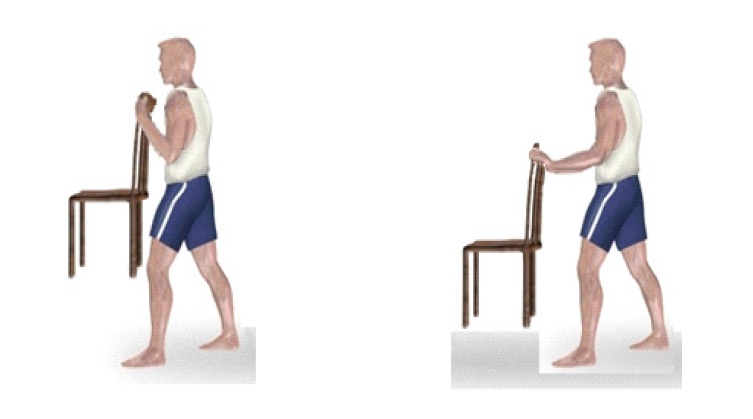
- Чтобы ощутить важность рычага силы, предлагаем читателям проделать следующий эксперимент: взять стул и попытаться удержать его одной рукой на весу, в одном случае руку прислонить к телу, в другом - выполнить задачу на прямой руке. Последнее для многих окажется непосильной задачей, хотя вес стула остался тем же самым.
Единицы измерения момента силы
Несколько слов также следует сказать о том, в каких единицах в СИ измеряется вращающий момент. Согласно записанной для него формуле, он измеряется в ньютонах на метр (Н*м). Однако в этих единицах также измеряется работа и энергия в физике (1 Н*м = 1 джоуль). Джоуль для момента M¯ не применяется, поскольку работа является скалярной величиной, M¯ же - это вектор.
Тем не менее совпадение единиц момента силы с единицами энергии не является случайным. Работа по вращению системы, совершенная моментом M, рассчитывается по формуле:
A = M*θ.
Откуда получаем, что M также может быть выражен в джоулях на радиан (Дж/рад).
Динамика вращения
В начале статьи мы записали кинематические характеристики, которые используются для описания движения вращения. В динамике вращения главным уравнением, которое использует эти характеристики, является следующее:
M = I*α.
Действие момента M на систему, имеющую момент инерции I, приводит к появлению углового ускорения α.

Данную формулу применяют, для определения угловых частот вращения в технике. Например, зная вращающий момент асинхронного двигателя, который зависит от частоты тока в катушке статора и от величины изменяющегося магнитного поля, а также зная инерционные свойства вращающегося ротора, можно определить, до какой скорости вращения ω раскручивается ротор двигателя за известное время t.
Пример решения задачи
Невесомый рычаг, длина которого составляет 2 метра, посередине имеет опору. Какой вес следует положить на один конец рычага, чтобы он находился в состоянии равновесия, если с другой стороны опоры на расстоянии 0,5 метра от нее лежит груз массой 10 кг?

Очевидно, что равновесие рычага наступит, если моменты сил, создаваемые грузами, будут равны по модулю. Сила, создающая момент в данной задаче, представляет собой вес тела. Рычаги силы равны расстояниям от грузов до опоры. Запишем соответствующее равенство:
M1 = M2 =>
m1*g*d1 = m2*g*d2 =>
P2 = m2*g = m1*g*d1/d2.
Вес P2 получим, если подставим из условия задачи значения m1 = 10 кг, d1 = 0,5 м, d2 = 1 м. Записанное равенство дает ответ: P2 = 49,05 ньютона.


























