В геометрии после точки прямая линия, пожалуй, является самым простым элементом. Его используют при построении любых сложных фигур на плоскости и в трехмерном пространстве. В данной статье рассмотрим общее уравнение прямой и решим пару задач с его использованием. Приступим!
Прямая линия в геометрии
Каждый знает, что такие фигуры, как прямоугольник, треугольник, призма, куб и так далее образованы пересекающимися прямыми линиями. Под прямой в геометрии считается одномерный объект, который может быть получен путем переноса определенной точки на имеющий одно и то же или противоположное направление вектор. Чтобы лучше понять это определение, представим, что имеется некоторая точка P в пространстве. Возьмем произвольный вектор u¯ в этом пространстве. Тогда любая точка Q прямой может быть получена в результате следующих математических операций:
Q = P + λ*u¯.
Здесь λ - это произвольное число, которое может быть положительным и отрицательным. Если равенство выше записать через координаты, то мы получим следующее уравнение прямой:
(x, y, z) = (x0, y0, z0) + λ*(a, b, c).
Это равенство называется уравнением прямой в векторной форме. А вектор u¯ называется направляющим.
Общее уравнение прямой на плоскости
Каждый школьник без каких-либо трудностей сможет записать его. Но чаще всего уравнение записывается так:
y = k*x + b.
Где k и b - произвольные числа. Число b называют свободным членом. Параметр k равен тангенсу угла, образованного пересечением прямой с осью абсцисс.
Приведенное уравнение выражено относительно переменной y. Если же его представить в более общем виде, тогда получим следующую форму записи:
A*x + B*y + C = 0.
Нетрудно показать, что эта форма записи общего уравнения прямой на плоскости легко преобразуется в предыдущий вид. Для этого левую и правую части следует разделить на коэффициент B и выразить y.
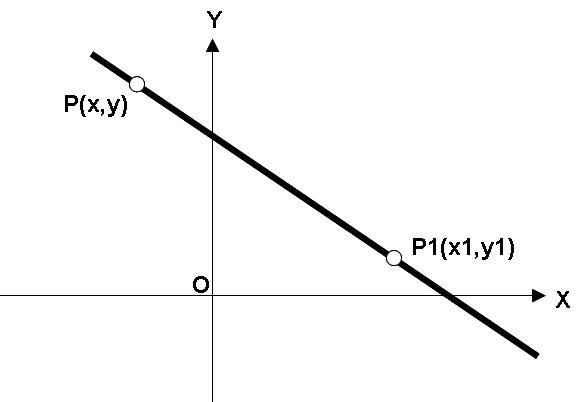
Выше на рисунке показана прямая, проходящая через две точки.
Прямая в трехмерном пространстве
Продолжим наше изучение. Мы рассмотрели вопрос, как задается на плоскости уравнение прямой в общей форме. Если мы приведенную в предыдущем пункте статьи форму записи применим для пространственного случая, что у нас получится? Все просто - уже не прямая, а плоскость. Действительно, следующее выражение описывает плоскость, которая параллельна оси z:
A*x + B*y + C = 0.
Если C=0, то такая плоскость проходит через ось z. Это важная особенность.
Как же быть тогда с общим уравнением прямой в пространстве? Чтобы понять, как его задать, нужно кое-что вспомнить. Две плоскости пересекаются по определенной прямой линии. Что это означает? Лишь то, что общим уравнением является результат решения системы из двух уравнений для плоскостей. Запишем эту систему:
- A1*x + B1*y + C1*z + D1 = 0;
- A2*x + B2*y + C2*z + D2 = 0.
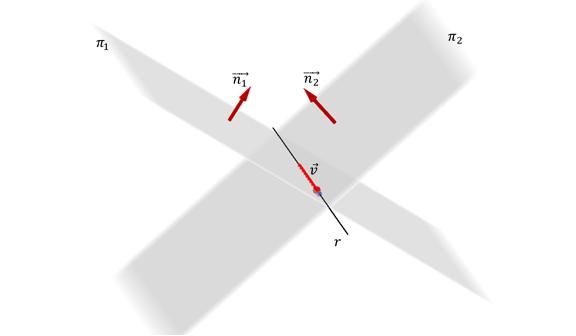
Эта система является общим уравнением прямой в пространстве. Заметим, что плоскости не должны быть параллельны друг другу, то есть их нормальные векторы должны быть наклонены под некоторым углом относительно друг друга. В противном случае система не будет иметь решений.
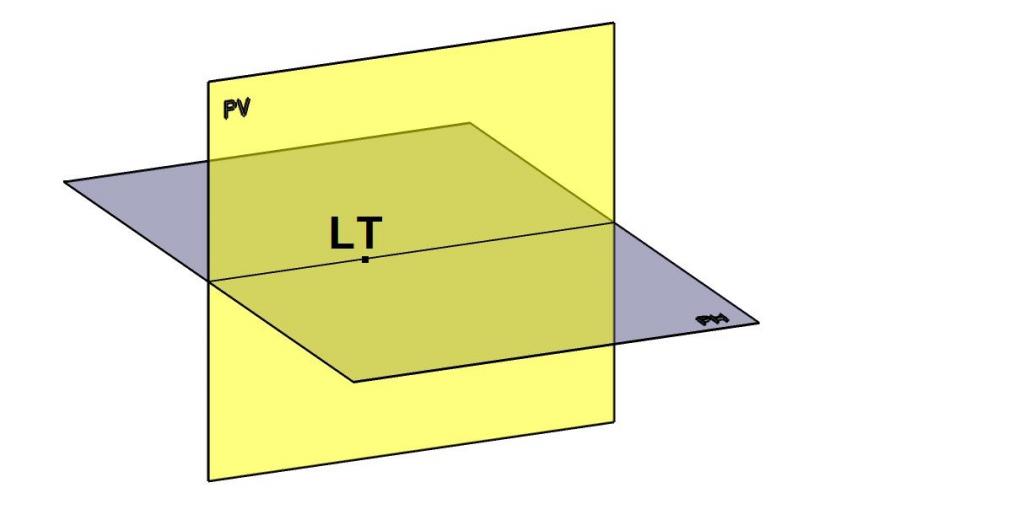
Выше мы приводили векторную форму записи уравнения для прямой линии. Ее удобно использовать при решении данной системы. Для этого сначала следует найти векторное произведение нормалей данных плоскостей. Результатом этой операции будет направляющий вектор прямой. Затем, следует вычислить любую точку, принадлежащую прямой. Для этого нужно положить любую из переменных равной определенному значению, две оставшиеся переменные найдутся путем решения приведенной системы.
Как перевести векторное уравнение в общее? Нюансы
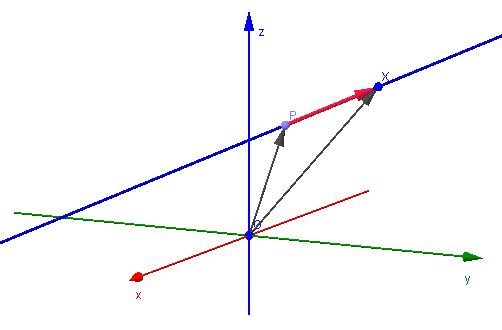
Это актуальная задача, которая может возникнуть, если следует написать общее уравнение прямой по известным координатам двух точек. Покажем, как решается эта задача на примере. Пусть известны координаты двух точек:
- P = (x1, y1);
- Q = (x2, y2 ).
Уравнение в векторной форме составить достаточно просто. Координаты направляющего вектора равны:
PQ = (x2-x1, y2-y1).
Заметим, что нет никакой разницы, если из координат точки P вычитать координаты Q, вектор лишь изменит свое направление на противоположное. Теперь следует взять любую точку и записать векторное уравнение:
(x, y ) = (x1, y1) + λ*(x2-x1, y2-y1).
Чтобы написать общее уравнение прямой, следует выразить в обоих случаях параметр λ. А затем приравнять полученные результаты. Имеем:
x = x1 + λ*(x2-x1) => λ = (x-x1)/(x2-x1);
y = y1 + λ*(y2-y1) => λ = (y-y1)/(y2-y1) =>
(x-x1)/(x2-x1) = (y-y1)/(y2-y1).
Остается только раскрыть скобки и перебросить все слагаемые уравнения в одну сторону равенства, чтобы получить общее выражение для прямой, проходящей через две известные точки.
В случае трехмерной задачи алгоритм решения сохраняется, только его результатом будет система из двух уравнений для плоскостей.
Задача
Необходимо составить общее уравнение прямой, которая пересекает ось x в точке (-3, 0), и которая параллельна оси y.
Начнем решение задачи с написания уравнения в векторной форме. Поскольку прямая параллельна оси ординат, то направляющим для нее вектором будет следующий:
u¯ = (0, 1).
Тогда искомая прямая запишется таким уравнением:
(x, y) = (-3, 0) + λ*(0, 1).
Теперь переведем это выражение в общую форму, для этого выразим параметр λ:
- x = -3;
- y = λ.
Таким образом, любое значение переменной y принадлежит прямой, однако, только единственное значение переменной x ей соответствует. Поэтому общее уравнение примет форму:
x + 3 = 0.
Задача с прямой в пространстве
Известно, что две пересекающиеся плоскости заданы следующими уравнениями:
- 2*x + y - z = 0;
- x - 2*y + 3 = 0.
Необходимо найти векторное уравнение прямой, по которой эти плоскости пересекаются. Приступим.
Как было сказано, общее уравнение прямой в трехмерном пространстве у нас уже задано в виде системы из двух с тремя неизвестными. В первую очередь определим направляющий вектор, по которой плоскости пересекаются. Умножая векторно координаты нормалей к плоскостям, получаем:
u¯ = [(2, 1, -1)*(1, -2, 0)] = (-2, -1, -5).
Поскольку умножение вектора на отрицательное число изменяет его направление на противоположное, то можно записать:
u¯ = -1*(-2, -1, -5) = (2, 1, 5).
Чтобы найти векторное выражение для прямой, помимо направляющего вектора, следует знать какую-нибудь точку этой прямой. Найти поскольку ее координаты должны удовлетворять системе уравнений в условии задачи, то найдем их. Положим для примера x = 0, тогда получим:
y = z;
y = 3/2 = 1,5.
Таким образом, принадлежащая искомой прямой точка имеет координаты:
P = (0, 1,5, 1,5).
Тогда получаем ответ на данную задачу, векторное уравнение искомой прямой будет иметь вид:
(x, y, z) = (0, 1,5, 1,5) + λ*(2, 1, 5).
Правильность решения можно легко проверить. Для этого необходимо выбрать произвольное значение параметра λ и подставить полученные координаты точки прямой в оба уравнения для плоскостей, получится тождество в обоих случаях.


























