Дифференцирование формул является важным математическим инструментом, позволяющим находить производные функций. Это открывает новые возможности для анализа и расчета различных процессов и зависимостей. Рассмотрим основные преимущества и способы применения дифференцирования формул.
Во-первых, дифференцирование позволяет найти скорость изменения функции в заданной точке. Это важно для понимания динамики процессов в физике, химии, экономике и других областях. Зная производную, можно определить в каких точках функция возрастает или убывает, где ее экстремумы.

Использование производных для оптимизации и моделирования
Производные широко используются при решении оптимизационных задач - поиске экстремумов функций при наличии ограничений. Это позволяет находить оптимальные решения в экономике, логистике, инженерии. Например, минимизировать затраты или максимизировать прибыль. Также производные незаменимы при математическом моделировании - описании реальных процессов уравнениями для прогнозирования и управления.
Вычисление пределов с помощью дифференцирования
Еще одно важное применение - вычисление пределов функций, в том числе для непрерывных процессов. Например, предельный объем газа при стремлении давления к нулю. Здесь также используют производные, применяя правила Лопиталя. Это позволяет находить пределы для сложных функций, которые нельзя вычислить другими способами.
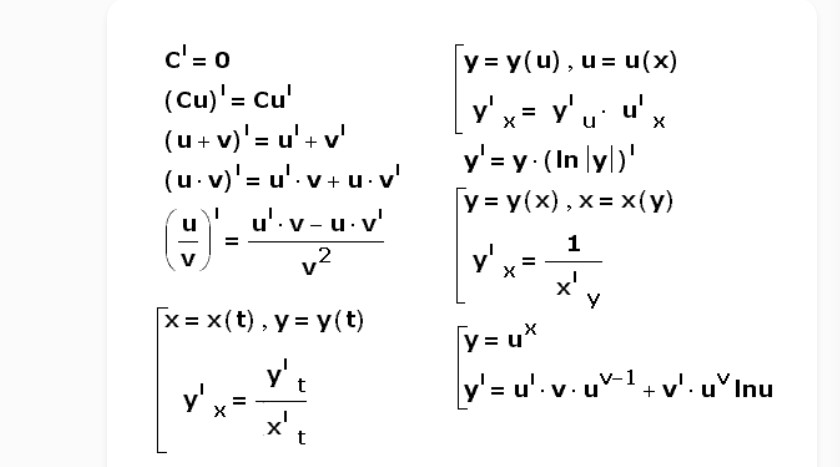
Дифференцирование в машинном обучении и искусственном интеллекте
Производные формул широко используются в современных алгоритмах машинного обучения и нейросетей. Они позволяют эффективно находить оптимальные веса нейронных сетей в процессе обучения. Благодаря дифференцированию создаются все более точные модели для прогнозирования, распознавания образов и обработки естественного языка.

Численные методы дифференцирования
Помимо аналитического дифференцирования существуют численные методы. Они позволяют находить производные функций, заданных таблично или графически. К численным методам относятся: метод конечных разностей, комплексные переменные, автоматическое дифференцирование. Эти методы актуальны при работе с экспериментальными данными или сложными моделями.
Инструменты для дифференцирования
Существует множество программных инструментов, упрощающих работу с дифференцированием формул. Это математические пакеты (Mathematica, Maple, Matlab), библиотеки для языков программирования (NumPy, SymPy, PyTorch). Они позволяют как символьно дифференцировать функции, так и численно находить производные. Использование таких инструментов значительно ускоряет вычисления.
Таким образом, дифференцирование формул открывает широкие возможности анализа и оптимизации в различных областях. Современные численные методы и программные инструменты делают эти возможности доступными для решения прикладных задач.
Применение дифференцирования в физике
Одной из важнейших областей применения дифференцирования является физика. С помощью производных можно описать скорость и ускорение движения тел. Производные используются в уравнениях механики, электродинамики, термодинамики. Например, второй закон Ньютона связывает ускорение тела с действующей на него силой через производную от скорости по времени.
Дифференциальные уравнения, содержащие производные, позволяют описать колебания струны, распространение волн, движение жидкостей и газов. Решение таких уравнений дает возможность моделировать и прогнозировать различные физические процессы. Дифференцирование необходимо при выводе большинства законов физики, начиная с законов Ньютона и заканчивая уравнениями квантовой механики.
Применение дифференцирования в химии и биологии
Дифференцирование также применяется в химии и биологии при моделировании сложных систем. С его помощью описывают кинетику химических реакций, процессы диффузии, теплопередачи. Производные используются для нахождения скорости химических превращений в зависимости от температуры, давления, концентрации.
В биологии дифференциальные уравнения помогают моделировать динамику популяций, клеточных процессов, распространения вирусов. Производные по времени описывают скорость роста популяций, скорость протекания биохимических реакций. Дифференцирование необходимо для понимания механизмов регуляции в живых организмах.
Таким образом, дифференцирование формул необходимо для построения математических моделей процессов во многих естественных науках - от физики до биологии. Это позволяет глубже изучать закономерности окружающего мира.
Применение дифференцирования в экономике
Дифференцирование широко используется в экономических исследованиях и моделировании. Экономисты применяют производные для анализа предельных издержек, предельной выручки, предельной полезности. Это помогает принимать оптимальные решения о объемах производства и ценообразовании.
С помощью дифференциальных уравнений описывают динамику спроса и предложения, колебания экономических показателей. Производные используются для анализа эластичности спроса по цене, доходу, перекрестной эластичности. Это важно для прогнозирования отклика рынка на ценовые изменения.
Дифференцирование в финансовом моделировании
В финансовой математике дифференцирование применяется при моделировании стоимости ценных бумаг, курсов валют, процентных ставок. Производные используются для оценки волатильности и рисков финансовых инструментов. Это позволяет строить оптимальные инвестиционные портфели и хеджировать риски.
Дифференциальные уравнения с производными по времени описывают динамику стоимости активов в моделях типа Блэка-Шоулза. Такие модели широко используются для оценки опционов, фьючерсов и других производных финансовых инструментов.
Дифференцирование при решении оптимизационных задач
Важнейшее применение дифференцирования - использование производных для решения различных оптимизационных задач в математике, экономике, инженерии. Производная позволяет найти точки минимума или максимума функции, что критически важно для поиска оптимального решения.
Методы оптимизации с использованием дифференцирования включают градиентный спуск, метод Ньютона, метод сопряженных градиентов. Они позволяют находить глобальный экстремум в условиях сложных ограничений. Эти методы лежат в основе современных алгоритмов машинного обучения.
Программная реализация дифференцирования
Современные языки программирования и математические пакеты имеют встроенные средства для вычисления производных и решения дифференциальных уравнений. Это значительно упрощает использование дифференцирования при решении прикладных задач.
Для аналитического дифференцирования используются символьные вычисления, реализованные в таких пакетах как Mathematica, Maple, Matlab. Численное дифференцирование реализуется средствами NumPy, TensorFlow, PyTorch и других библиотек.
Таким образом, благодаря программным средствам мощный аппарат дифференциального исчисления становится доступен инженерам, экономистам, ученым для решения прикладных задач в различных областях.


























