Как найти площадь треугольника на клетчатой бумаге с размером клетки 1х1

Знаете ли вы, как найти площадь треугольника, изображенного на клетчатой бумаге 1×1? Эта, казалось бы, простая задача может вызвать затруднения даже у опытных пользователей. В нашей новой статье мы подробно разберем методы вычисления площади треугольника на клетчатой бумаге 1х1 и дадим пошаговые инструкции для решения подобных задач. Читайте и узнавайте полезную информацию!

Основные способы нахождения площади треугольника

Существует несколько основных способов для нахождения площади треугольника на клетчатой бумаге:

• Использование стандартной формулы для площади треугольника через основание и высоту
• Применение формулы для прямоугольного треугольника через два катета
• Метод вычитания площадей более простых фигур из площади описанной фигуры
• Использование формулы Пика для приближенного подсчета количества клеток, покрывающих площадь фигуры

Рассмотрим подробнее каждый из этих способов.

Стандартная формула площади треугольника

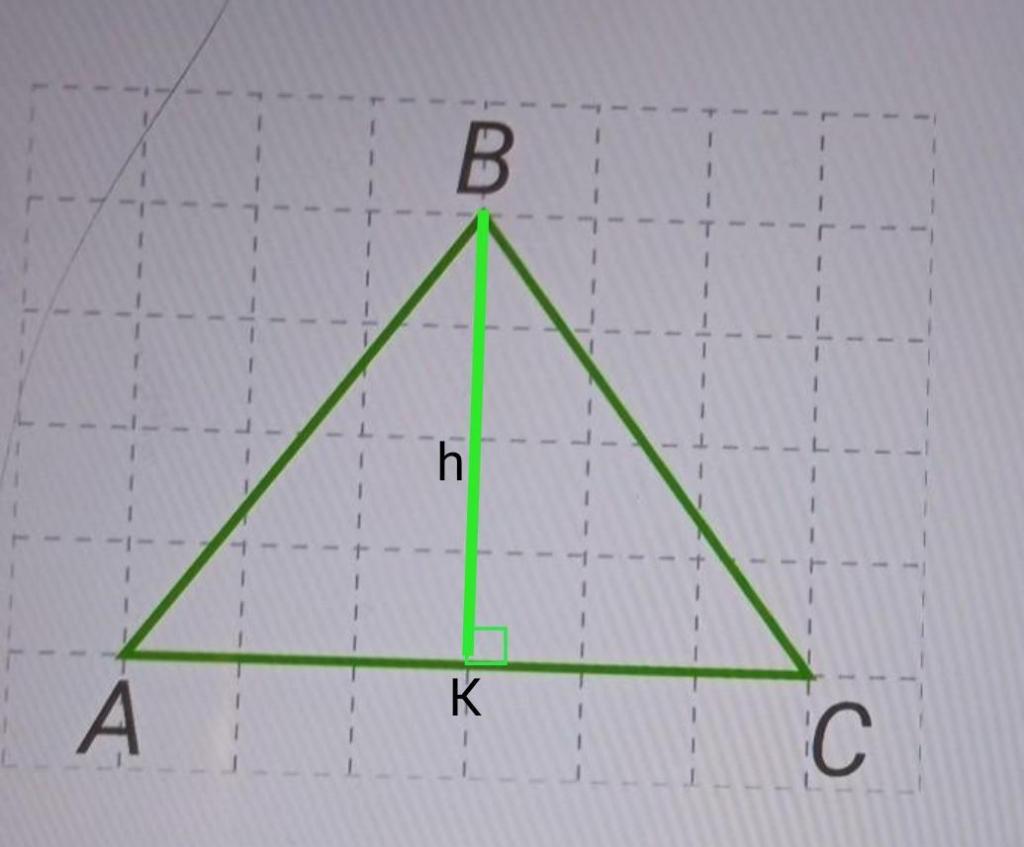
Основная формула для нахождения площади любого треугольника через основание и высоту к нему имеет следующий вид:

S = (a × h) / 2

где S - площадь треугольника, a - длина основания, h - соответствующая высота.

Чтобы воспользоваться этой формулой на клетчатой бумаге, нужно определить основание треугольника и высоту к нему в клетках, а затем подставить значения в формулу. Например, если основание равно 5 клеткам, а высота 3 клеткам, то:

S = (5 × 3) / 2 = 7,5 клеток

Но стоит помнить, что в стандартных тетрадях размер клетки составляет 0,5 см. Значит:

7,5 × 0,5 = 3,75 см

Формула для прямоугольного треугольника

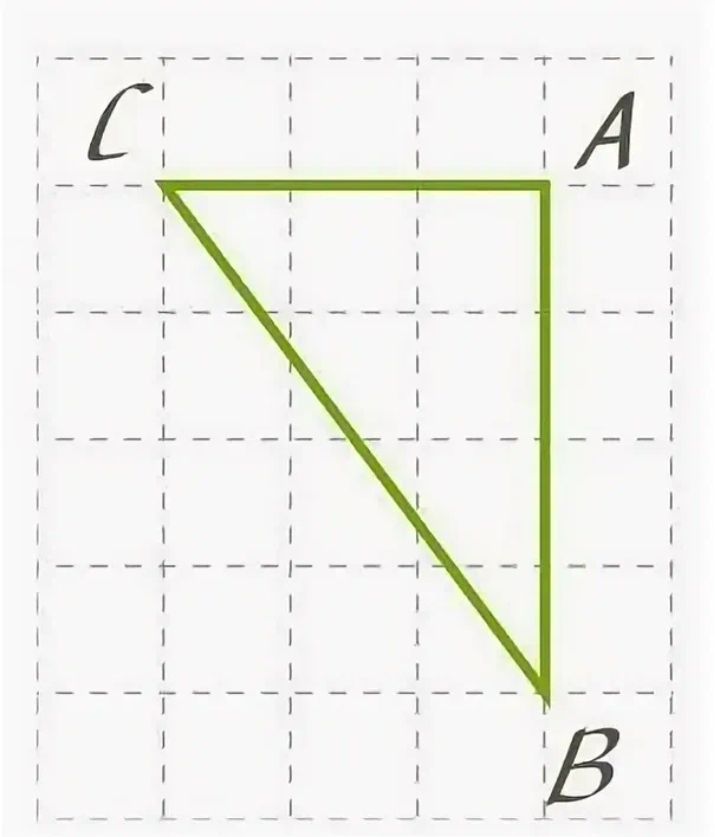
Как найти площадь прямоугольного треугольника на клетчатой бумаге 1х1? Если на клетчатой бумаге изображен прямоугольный треугольник, то для нахождения его площади используется формула:

S = (a × b) / 2

где a и b - длины катетов.

Например, если один катет равен 3 клеткам, а другой 5 клеткам, площадь прямоугольного треугольника будет равна:

S = (3 × 5) / 2 = 7,5 клеток (или 3,75 см)

Метод вычитания площадей

Иногда удобно использовать метод вычитания, когда площадь нужного нам треугольника находится как разность площадей более простых фигур.

Например, если треугольник вписан в прямоугольник, то можно вычесть из площади прямоугольника площади трех дополнительных прямоугольных треугольников:

Здесь площадь искомого треугольника ABC будет равна:

S_APK = S_ABCD - S_KCP - S_ABK - S_APD

Аналогично можно использовать вычитание и для других случаев.