Геометрия - на первый взгляд скучная наука со множеством формул и теорем. Но если разобраться, она позволяет решать массу практических задач из реальной жизни. Например, при строительстве, дизайне интерьера или даже при упаковке товаров часто нужно вычислять объемы разных фигур. Давайте разберемся, как с легкостью находить объем любого многогранника всего за пару минут!
Что такое многогранник и какие бывают типы
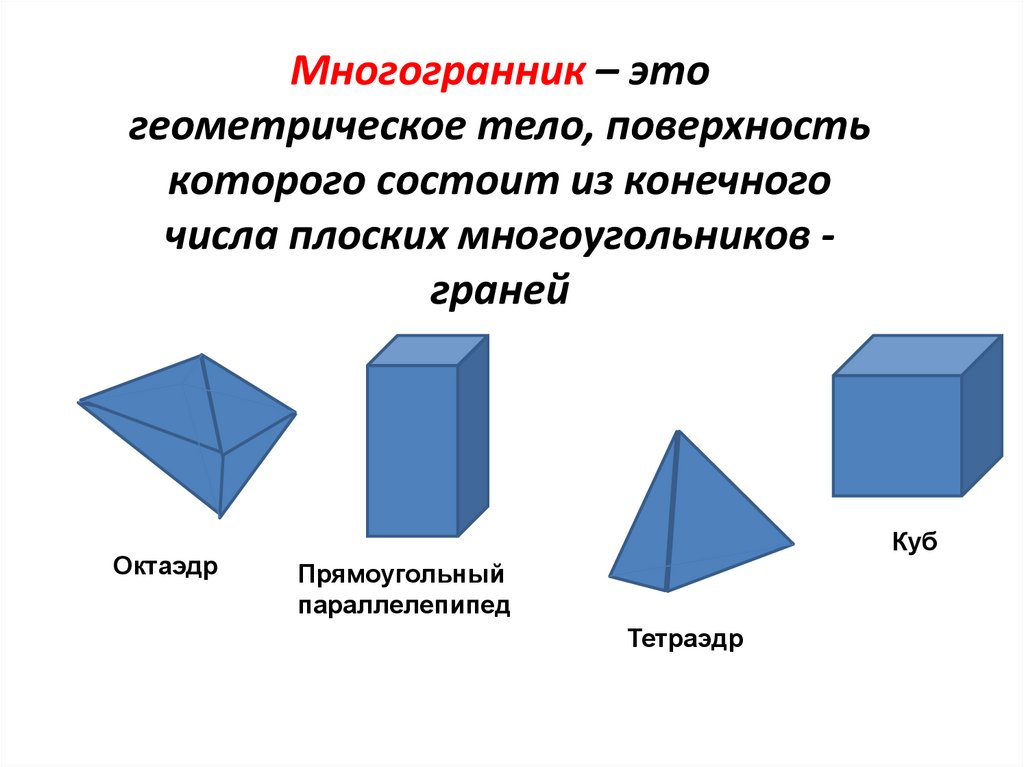
Многогранник - это геометрическое тело, ограниченное плоскими многоугольниками. Самые распространенные виды многогранников:
- Пирамида - многогранник, основанием которого служит многоугольник, а боковые грани сходятся в одной вершине
- Призма - многогранник, у которого две грани представляют собой параллельные равные многоугольники, а боковые грани - параллелограммы
- Параллелепипед - прямой призматический многогранник, у которого все грани являются параллелограммами
Как найти объем пирамиды
Объем любой пирамиды вычисляется по формуле:
V = (S осн * H) / 3
где Сосн - площадь основания пирамиды, H - высота пирамиды.
Как вычислить объем призмы
Формула объема призмы выглядит так:
V = S осн * H
Здесь S осн - площадь основания, Н - высота призмы. Для нахождения площади основания нужно сложить площади составляющих его фигур (чаще всего прямоугольников или треугольников).
Вычисление объема параллелепипеда
Параллелепипед - частный вид призмы. Для него формула объема такая же:
V = S осн * H
Но площадь основания параллелепипеда вычисляется проще, так как оно всегда представляет собой прямоугольник. Достаточно перемножить длины его сторон.
Пошаговый алгоритм вычисления объема многогранника

Итак, мы разобрали основные типы многогранников и формулы для нахождения их объемов. Чтобы быстро справиться с любой задачей на вычисление объема, достаточно придерживаться простого алгоритма:
- Определите тип многогранника (пирамида, призма, параллелепипед).
- По формуле найдите площадь его основания.
- Вычислите высоту многогранника.
- Подставьте значения площади основания и высоты в соответствующую формулу объема.
Следуя этим четырем шагам, можно с легкостью справиться с любой задачей всего за пару минут! Теперь вы знаете, как быстро и верно найти объем многогранника нужной формы. Успехов в решении геометрических задач!
Пример вычисления объема треугольной пирамиды
Давайте рассмотрим конкретный пример вычисления объема треугольного многогранника - треугольной пирамиды. Пусть длина ребер основания равны 6 и 4 см, а высота пирамиды - 8 см.
- Находим площадь основания по формуле площади правильного треугольника: S осн = (ab) / 2, где a и b- стороны треугольника. S осн = (6 × 4) / 2 = 12 см2
- Подставляем значения в формулу объема пирамиды: V = (Сосн * H) / 3 = (12 см2 * 8 см) / 3 = 32 см^3
Получаем, что объем данной пирамиды равен 32 см3.
Как найти объем многогранника: обобщение методики
Как видно из примера выше и предыдущего материала, общая методика вычисления объема любого многогранника такова:
- Определяем тип многогранника.
- Находим площадь его основания (если многогранник - пирамида или призма).
- Вычисляем высоту многогранника.
- Подставляем найденные значения в соответствующую формулу для данного типа многогранника.
Где применяются навыки вычисления объемов
Умение быстро и точно находить объем многогранника понадобится:
- Архитекторам и строителям
- Инженерам и конструкторам
- Дизайнерам интерьера и ландшафта
- Людям, планирующим ремонт или отделку помещения
- Тем, кто занимается расчетами для 3D-печати или прототипирования
Разбор типовой задачи на нахождение объема
Для закрепления материала рассмотрим следующую типовую задачу:
Дан параллелепипед со сторонами 4 см, 6 см и 8 см. Найдите объем многогранника.
Решение:
- Определяем, что многогранник - параллелепипед.
- Находим площадь основания: S осн = a * b = 4 * 6 = 24 см2.
- Задана высота параллелепипеда: H = 8 см.
- Подставляем значения Сосн и H в формулу объема параллелепипеда: V = S осн * H = 24 см2 * 8 см = 192 см3
- Ответ: 192 см3.
Как видно, алгоритм решения простой и универсален для любых задач такого типа. Главное - правильно определить вид многогранника и знать соответствующую формулу.






















