Знали ли вы, что от длины одной единственной линии в пространстве может зависеть решение множества задач? Этой волшебной линией является диагональ правильной четырехугольной призмы. В нашей новой статье вы узнаете, что такое диагональ, как ее найти для любой заданной призмы и как использовать полученное знание с максимальной пользой на практике. Приглашаем вас в увлекательное путешествие в мир геометрии!
Основные понятия
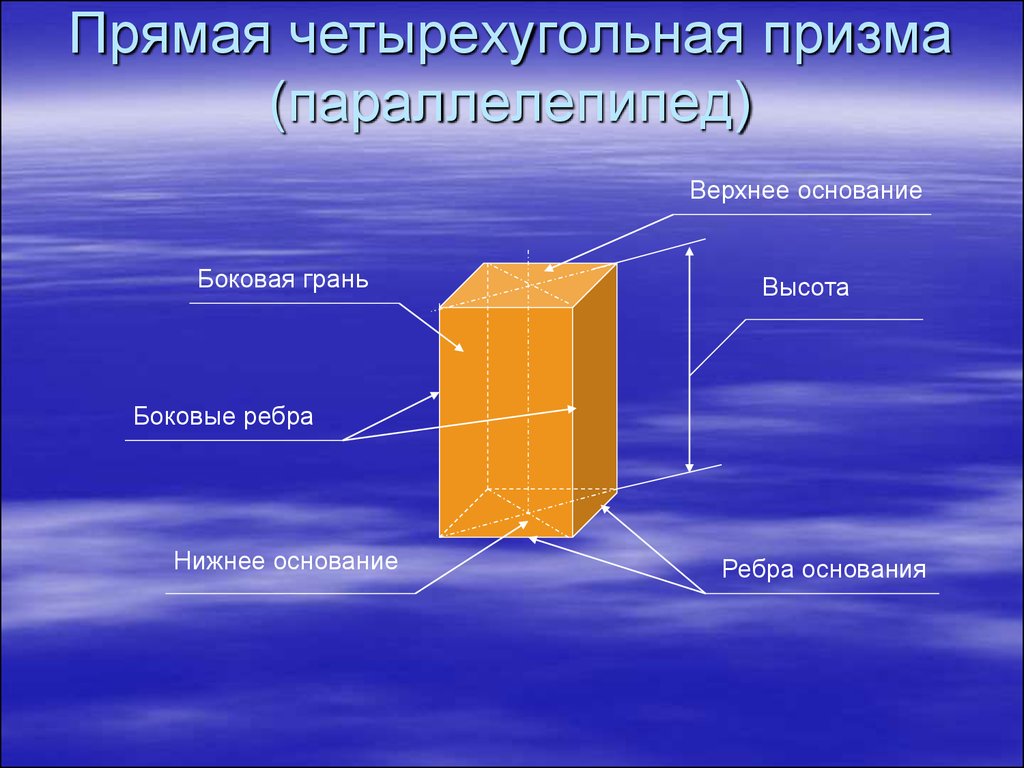
Давайте разберемся, что представляет собой правильная четырехугольная призма. Это геометрическое тело имеет следующие характеристики:
- Два одинаковых четырехугольника-основания, лежащих в параллельных плоскостях
- Четыре прямоугольные грани-боковины, соединяющие вершины оснований
- Четыре вершины, в которых сходятся ребра боковин и оснований
- Ребра и грани перпендикулярны основаниям
Конкретным примером такой призмы может служить коробка с квадратным дном или крышкой. Теперь давайте определим, что такое диагональ. Это отрезок, соединяющий две вершины геометрической фигуры. В случае с призмой диагональ проходит из одной вершины основания в противолежащую вершину другого основания:
A_____________________B
↓ ↓ ↓
│ ↓ │
│ ↓ Диагональ│
│ ↓ │
↓ ↓ ↓
D____________________C
Формула для нахождения диагонали
Итак, как найти диагональ правильной четырехугольной призмы? Для этого используется формула, выводимая из теоремы Пифагора:
Диагональ = √(Сторона2 + Высота2)
Где Сторона - длина стороны основания (квадрата), а Высота - расстояние между основаниями. Давайте разберем подробный пример вычисления диагонали для призмы со стороной основания 6 см и высотой 8 см:
- Подставляем значения в формулу:
Диагональ = √(62 + 82) = √(36 + 64) - Складываем квадраты сторон:
√(36 + 64) = √100 - Извлекаем корень:
√100 = 10 (см)
Получаем, что диагональ равна 10 см. Аналогично можно вычислить диагональ для любой заданной правильной четырехугольной призмы, зная сторону основания и высоту.
Теперь вы знаете, что такое диагональ призмы, как ее найти и для чего она нужна. Далее мы разберем, как диагонали правильной четырехугольной призмы применяются на геометрических задач.
Диагональ правильной четырехугольной призмы является одним из ключевых элементов при решении множества задач на вычисление различных характеристик этого геометрического тела.
В частности, по длине диагонали можно найти:
- Объем призмы по формуле:
V = d2 * h / 2, где d - диагональ, h - высота - Площадь полной поверхности:
S = 2 * (a2 + ab), где a - сторона основания, b - диагональ - Площадь боковой поверхности:
S = 2ab + 2ah, где h - высота
Рассмотрим задачу на применение диагонали для нахождения объема призмы:
Дана правильная четырехугольная призма со стороной основания 5 см и высотой 12 см. Найдите ее объем, если известно, что длина диагонали равна 13 см.
Решение:
- По теореме Пифагора находим высоту призмы:
h = √(132 - 52) = √(169 - 25) = √144 = 12 (см) - Подставляем значения d и h в формулу объема:
V = 132 * 12 / 2 = 338 (куб.см)
Применение диагонали для нахождения площадей
Помимо объема, знание длины диагонали правильной четырехугольной призмы позволяет также находить ее площади — полной поверхности и боковой поверхности. Рассмотрим примеры.
Задача 1
Дана призма со стороной основания 3 см. Диагональ равна 5 см. Найдите площадь полной поверхности призмы.
Решение. Подставляем значения в формулу площади полной поверхности:
S = 2 * (32 + 3*5) = 2 * (9 + 15) = 48 (кв. см)
Задача 2
У призмы высота 10 см, сторона основания 4 см. Диагональ равна 12 см. Найдите площадь боковой поверхности.
Решение. Подставляем в формулу площади боковой поверхности:
S = 2*4*12 + 2*4*10 = 96 + 80 = 176 (кв. см)
Применение для нахождения углов
Используя теорему Пифагора и зная длину диагонали правильной четырехугольной призмы, можно также находить величины некоторых углов в этой призме.
Задача 3
Дана призма с диагональю 13 см. Найдите угол между диагональю и плоскостью боковой грани.
Решение. По теореме Пифагора:
132 = x2 + x2
Отсюда x = 13 / √2. Значит, искомый угол равен arccos(x / 13) = arccos(1 / √2) = 45°.























