В статье подробно описывается, как найти точки максимума и минимума функции. Рассматриваются основные теоретические сведения, этапы алгоритма нахождения экстремумов, приводятся разобранные примеры для разных типов функций. Освещаются особые случаи, когда функция задана неявно или графически. Даются практические советы, рекомендуются полезные ресурсы для самостоятельного изучения темы поиска точек экстремума. В интерактивном тренажере можно потренировать навыки решения подобных задач.
Основные понятия
Точка максимума функции - это точка, в которой функция принимает наибольшее значение. В этой точке график функции имеет "вершину". Точка минимума функции - наоборот, точка, где функция принимает наименьшее значение и график имеет "впадину".
Согласно основной теореме математического анализа, если функция имеет экстремум (максимум или минимум) в некоторой точке, то в этой точке ее производная равна нулю или не существует.
Алгоритм нахождения точек экстремума
- Найти производную функции
- Приравнять производную к нулю и решить это уравнение
- Найти точки, в которых производная не существует (если есть)
- Исследовать знаки производной на интервалах между найденными точками
- Определить точки максимума и минимума по теореме
Примеры решения задач:

Линейная функция
Найдите точки максимума функции на графике y = 2x + 5.
Решение. Производная функции y' = 2 - константа. Она никогда не равна нулю. Значит, данная линейная функция не имеет ни точек максимума, ни точек минимума. Она возрастает на всей числовой прямой.
Квадратичная функция
Найдите точку максимума функции y = x2 - 4x - 5.
Решение. Находим производную: y' = 2x - 4. Приравниваем ее к нулю: 2x - 4 = 0, x = 2. Это точка максимума, так как при переходе через нее производная меняет знак с "+" на "-".

Тригонометрическая функция
Найдите точки максимума функции y = 3cos(x).
Решение. Производная: y' = -3sin(x). Она обращается в ноль при x = 0 и x = π. В точке x = π/2 производная меняет знак с "-" на "+", значит это точка минимума функции. А в точке 0 наоборот - с "+" на "-", то есть эта точка является точкой максимума.
Особые случаи: Функция задана неявно
Рассмотрим случай, когда функция задана неявно, например уравнением: x3 + y3 = 25
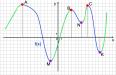
Найдите точки максимума функции на графике.По графику видно, что имеются две точки максимума: x ≈ -2 и x ≈ 3. А точки минимума - при x ≈ -4 и x ≈ 1.
Типичные ошибки
Ошибки при нахождении точек экстремума чаще всего бывают связаны с неправильным решением уравнения производной. Рассмотрим несколько примеров.
Неверное решение уравнения производной
Например, при решении уравнения, нельзя просто взять и вычеркнуть одинаковые множители 3x. Необходимо предварительно разложить левую часть на множители.
Промежутки монотонности вместо точек экстремума
Бывают случаи, когда вместо нахождения конкретных точек максимума или минимума требуется найти промежутки, на которых функция возрастает или убывает. Для этого также используется производная.
Например, для функции y = x3 - 3x + 1 производная равна y' = 3x2 - 3. Приравнивая ее к нулю, видим, что точек экстремума нет. Но зато функция возрастает при x > 1 и убывает при x < 1.
Отрезки, на которых ищутся экстремумы
Иногда в задаче задается конкретный отрезок, на котором нужно найти точки экстремума функции. Например:
Найдите точки максимума и минимума функции f(x) = x3 - 3x2 - x на отрезке [-2; 3].
В этом случае помимо обычных точек экстремума нужно рассмотреть еще значения функции на концах отрезка, ведь максимум или минимум может достигаться в крайних точках.
Полезные приемы
При решении задач на нахождение экстремумов иногда удобно применять такие приемы:
- Замена переменной для упрощения производной
- Разложение сложной функции на простые множители
- Использование особенностей графика (периодичность, четность и т.д.)
Тренировка на примерах
Для закрепления навыков рекомендуется решать как можно больше разнообразных примеров задач на нахождение точек экстремума. Полезно также строить графики функций в процессе решения.
Ресурсы для самостоятельного изучения
Чтобы лучше разобраться в теме поиска точек экстремума функции, рекомендуется воспользоваться следующими ресурсами:
- Видеоуроки на популярных образовательных каналах в YouTube
- Статьи на сайтах подготовки к ЕГЭ
- Специализированные сайты-тренажеры с интерактивными задачами по теме
Такие ресурсы позволяют изучить материал в удобном формате и закрепить его с помощью практических заданий.
Интерактивный тренажер
Для закрепления материала предлагаем интерактивный тренажер с задачами на нахождение точек экстремума функции.
Тренажер позволяет:
- Генерировать задачи нужной сложности
- Давать подсказки при решении
- Показывать эталонное решение
- Анализировать ошибки пользователя
После прохождения тренажера можно проверить свои знания, ответив на вопросы небольшого теста.
Типичные примеры задач
Рассмотрим несколько типовых примеров задач на найдите точки максимума функции для самостоятельного решения:
-
Найдите точки максимума функции y = x3 - 3x + 1 на отрезке [-2; 5]
-
Найдите все экстремумы функции y = tg(x)
-
Найдите промежутки монотонности и точки экстремума функции y = ln(x2 + 1)
Аналогичным образом можно подобрать примеры и потренироваться в нахождении точек минимума функции, а также решать задачи на нахождение наибольших и наименьших значений функции на заданном отрезке.
Решение задач повышенной сложности
Рассмотрим примеры более сложных задач на нахождение точек экстремума функции.
-
Дана функция y = (x2 - 1) / (x - 1). Найдите все ее точки экстремума.
Решение. Несмотря на сложный вид дробно-рациональной функции, применим стандартный алгоритм.
-
Дана функция y = x3ln(x2 + 1). Найдите ее точки максимума и минимума.
Решение. Воспользуемся методом логарифмического дифференцирования.
-
Дана функция y = sin(x) / e^x. Найдите точки экстремума.
Решение. Преобразуем функцию для упрощения нахождения производной.
Такие задачи рекомендуется решать в несколько этапов, применяя изученные приемы преобразования и упрощения функций.
Проверка знаний
После изучения материала можно проверить полученные знания и навыки, ответив на несколько контрольных вопросов:
- Что такое точки экстремума функции?
- Как связаны точки экстремума и производная функции?
- Перечислите основные этапы алгоритма нахождения точек максимума/минимума
Такая самопроверка поможет выявить пробелы и недопонимание материала.
Разбор типичных ошибок
Давайте разберем некоторые типичные ошибки, которые встречаются при решении задач на нахождение точек экстремума функции.
Ошибка 1. Неправильное решение уравнения производной
Рассмотрим функцию y = x^3 - 3x + 1. Ее производная имеет вид y' = 3x^2 - 3. Приравнивая производную к нулю и решая уравнение, получаем:
Однако решение x = ±1 является неверным, поскольку мы неправильно решили уравнение, вынеся за скобки один из множителей.
Ошибка 2. Пропуск критических точек
Рассматривая функцию y = |x|, мы находим, что ее производная во всех точках либо положительна, либо отрицательна. Поэтому критических точек у данной функции нет.
Однако это неверно! Мы пропустили точку x = 0, в которой производная не определена. Это и есть критическая точка функции.
Ошибка 3. Неверная проверка знаков производной
Пусть дана функция y = x^4 - 8x^2 + 16. При решении мы можем вычислить значения производной в разных точках и ошибочно сделать вывод, что функция возрастает при любых значениях x.
Однако на самом деле производная меняет знак в точках x = ±2, поэтому здесь есть экстремумы.