Казалось бы, параллелограмм – самая обычная геометрическая фигура. Но простая на первый взгляд формула для вычисления его площади таит в себе удивительную историю открытий и доказательств. Приглашаем вас в это захватывающее путешествие!
Историческая справка об открытии формулы
Впервые формула для вычисления площади параллелограмма появилась в трудах древнегреческого математика Евклида примерно в 300 году до нашей эры. Основываясь на более ранних открытиях своих предшественников о свойствах треугольников и параллельных линий, Евклид смог строго доказать, что площадь параллелограмма равна произведению длины одной его стороны (основания) и высоты, проведенной к этой стороне.
Площадь параллелограмма = Основание × Высота (a*h)
Это открытие произвело настоящую революцию в геометрии тех времен! Ведь теперь появилась возможность вычислять площадь такой сложной на первый взгляд фигуры, как параллелограмм. Правда, современники Евклида по-разному отнеслись к этому достижению. Одни восхищались строгостью выводов, другие сомневались в правильности формулы. Поэтому Евклиду пришлось приложить немало усилий, чтобы убедить коллег в справедливости своего открытия.
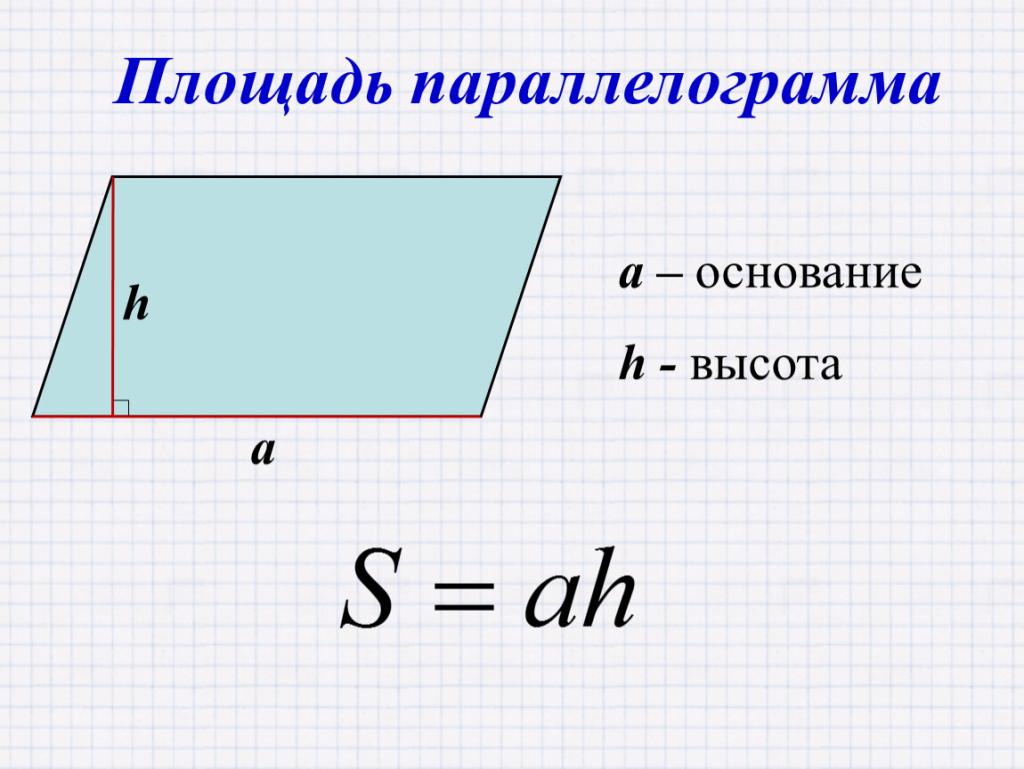
Вывод формулы площади параллелограмма
Для вывода формулы Евклид использовал такие свойства параллелограмма:
- Противоположные стороны параллельны и равны между собой
- Диагонали делят параллелограмм на два равных треугольника
Рассмотрим параллелограмм ABCD, в котором проведена диагональ BD:
Диагональ делит его на два равных треугольника ABD и CDB. Поскольку эти треугольники равны, площадь параллелограмма в 2 раза больше площади любого из них:
Sпараллелограмма = 2·Sтреугольника
Но из геометрии треугольников было известно, что его площадь равна половине произведения основания на высоту. Подставляя это выражение и проводя преобразования, Евклид получил искомую формулу:
Таким образом, формула площади параллелограмма была строго доказана!
Применение формулы через синус угла
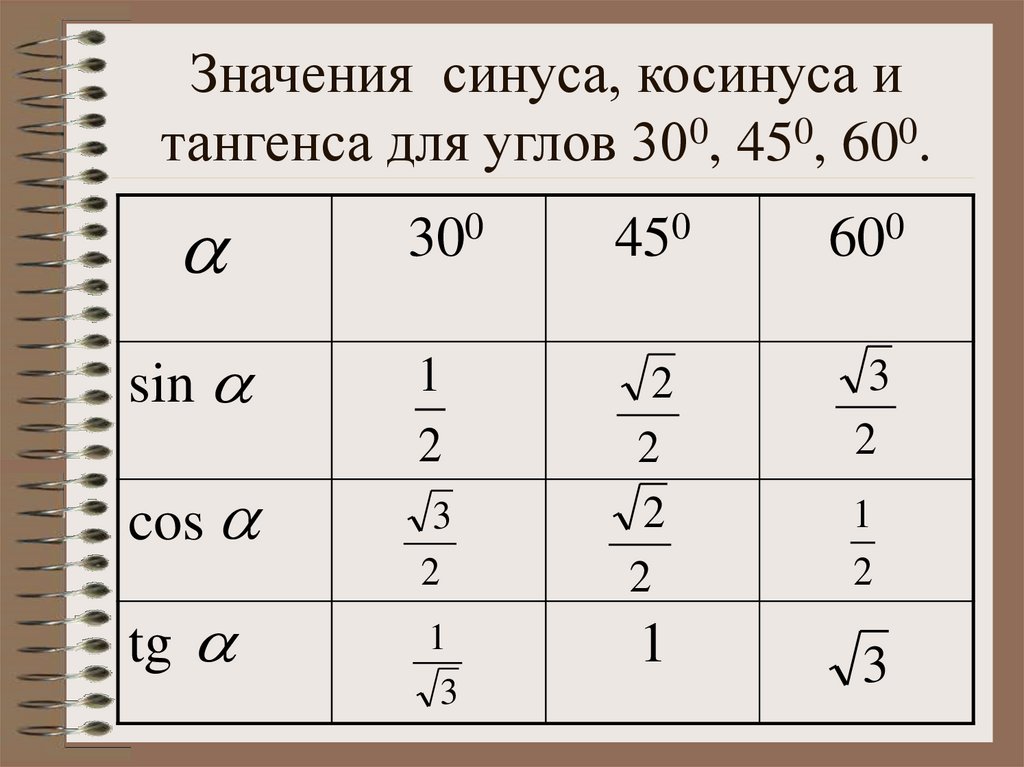
На практике чаще всего используют две основные формулы для вычисления площади параллелограмма:
- Через основание и высоту
- Через стороны и угол между ними
Рассмотрим конкретный пример:
| Длина стороны AD: | 10 см |
| Длина стороны DC: | 20 см |
| Угол между ними: | 54° |
Найдем площадь параллелограмма ABCD.
В данном случае удобнее использовать вторую формулу, поскольку нам известны длины сторон и угол между ними. Подставляя значения, в формулу S = a · b · sin α, получаем:
10 * 20 * 0,5 = 100
Площадь искомого параллелограмма равна 100 см2
Формула периметра параллелограмма
Кроме площади, для параллелограмма можно также легко найти периметр. Он равен:
- Сумме всех сторон
- Удвоенной сумме смежных сторон (основания и высоты)
Например, если основание равно 5 см, а высота 7 см, то периметр составит 2·(5 + 7) = 24 см.
Практические советы
Чтобы легко запомнить формулу площади параллелограмма, можно использовать ассоциацию:
Можно представить параллелограмм в виде лодки. Тогда одна сторона будет ее "дном", а другая - "бортом". А высота - это "весло", которым "гребут". Чем сильнее и длиннее "весло", тем больше "лодка" продвигается вперед. То есть чем больше высота, тем больше площадь параллелограмма при одинаковом основании.
Решение задач на вычисление площади
При решении задач на вычисление площади параллелограмма важно:
- Внимательно изучить условие и определить, какие элементы даны
- Выбрать подходящую формулу в зависимости от имеющихся данных
- Аккуратно подставить значения в формулу и выполнить вычисления
- Проверить правильность полученного ответа
Чтобы быстрее ориентироваться при выборе формулы, рекомендуем заранее подготовить шпаргалку.
Где еще применима формула
Формула площади параллелограмма полезна не только в геометрии. Она также используется:
- При расчете площадей участков неправильной формы
- В инженерных задачах по определению размеров конструкций
- Для вычислений в экономике и статистике
Надеемся, теперь вы лучше понимаете, чему равна площадь параллелограмма. Успехов!






















