Деление на двузначное число часто вызывает затруднения у учеников начальной школы. Это связано с тем, что для нахождения частного приходится подбирать число, умножение которого на делитель даст делимое. В статье мы разберем основные приемы деления на двузначное число, рассмотрим примеры и выполним упражнения.
Деление на двузначное число можно выполнять с помощью различных приемов: методом подбора, используя взаимосвязь умножения и деления, опираясь на последние цифры делимого и делителя. Главное - понимать алгоритм и постоянно проверять результат умножением.
Освоив деление на двузначное число, вы значительно расширите свои математические умения. Это важный навык, который пригодится для решения многих практических задач. Приступим!
Метод подбора частного при делении на двузначное число
Деление на двузначное число может показаться сложным на первый взгляд. Однако существует эффективный метод решения таких примеров - метод подбора частного. Суть этого метода заключается в использовании взаимосвязи умножения и деления для поиска верного частного.
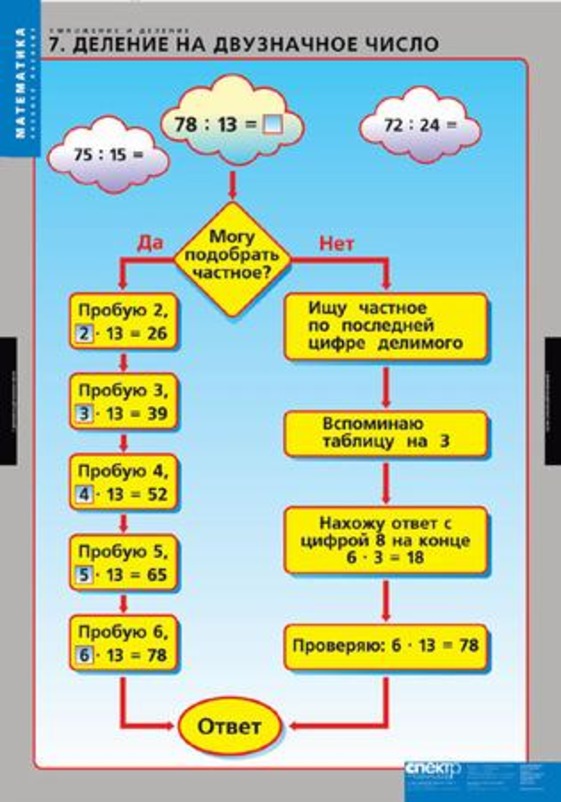
Рассмотрим на примере: нужно разделить число 48 на 12. Сначала мы пробуем в частном число 2 и проверяем - умножаем 12 на 2. Получается 24, это меньше 48, значит 2 не подходит. Далее пробуем число 3, умножаем 12 на 3 - получается 36, опять не подходит. И только когда мы пробуем число 4, умножение 12 на 4 дает 48 и мы понимаем, что нашли верное частное. Итак, алгоритм таков:
- Записываем пример на деление двузначного числа на двузначное
- Пробуем в частном последовательно разные числа, начиная с самых маленьких
- Каждый раз проверяем, умножая делитель на предполагаемое частное
- Выбираем то число, которое при умножении на делитель даст делимое
- Это число и есть частное
Применяя этот метод, можно научиться делить любые двузначные числа. Например:
| Делимое | Делитель |
| 66 | 22 |
| 78 | 26 |
| 99 | 33 |
В каждом случае по описанному выше алгоритму подбираем частное и проверяем его умножением на делитель. Деление двузначных чисел методом подбора частного может показаться непростым для начинающих, но при систематической тренировке этот навык быстро приходит. Главное - выработать четкое следование алгоритму и не пропускать этап проверки предполагаемого частного.
Также важно понимать, что метод подбора основан на использовании взаимосвязи между умножением и делением. Умножение позволяет проверить правильность найденного при делении частного. Это фундаментальное свойство умножения и деления широко применяется при вычислениях в математике.

Использование взаимосвязи умножения и деления
Деление и умножение - взаимосвязанные действия. Это значит, что зная результат умножения двух чисел, мы можем найти результат деления одного из этих чисел на другое. И наоборот, зная результат деления, мы можем восстановить исходное произведение.
Например, если известно, что 12 • 4 = 48, то, разделив 48 на 4, получим 12. Или, если дан результат деления 48 : 4 = 12, то, перемножив 4 и 12, вернемся к числу 48. Эта фундаментальная взаимосвязь широко используется в вычислительной математике. В частности, она является основой метода подбора частного при делении на двузначное число.
Рассмотрим пример деления 66 на 22. Согласно алгоритму метода подбора, мы пробуем различные числа в частном и для каждого проверяем, перемножая его с делителем. То есть, мы используем взаимосвязь: 22 • Х = 66 Находя такое число Х, чтобы вернуться к исходному делимому 66. В данном случае это число 3. Таким образом, благодаря свойству взаимосвязи, зная результат деления 66 : 22 = 3, мы можем восстановить исходное произведение 22 • 3 = 66.
Подобный подход применим для любого деления двузначных чисел. Рассмотрим еще один пример:
| Делимое | Делитель |
| 87 | 29 |
Согласно алгоритму: Пробуем число 2: 29 • 2 = 58 — не подходит Пробуем число 3: 29 • 3 = 87 — подошло Значит, 87 : 29 = 3 Проверим, перемножив: 29 • 3 = 87 Взаимосвязь результата деления и исходного произведения подтверждается. Благодаря этому свойству, мы можем не только выполнять деление двузначных чисел методом подбора, но и проверять правильность найденного результата.
Также отметим, что использование взаимосвязи позволяет решать и более сложные задачи, связанные с делением. Например, в текстовой задаче требуется узнать, во сколько раз одно число больше другого. Для этого нужно разделить большее число на меньшее. С помощью метода подбора и проверки умножением мы можем найти это отношение.
Или при решении уравнений, где известно произведение неизвестного и какого-то числа, а требуется найти само неизвестное. В этом случае делим обе части уравнения на известный множитель и получаем искомое число. Таким образом, понимание фундаментальной взаимосвязи умножения и деления весьма полезно для овладения всем спектром вычислительных задач в математике.
Опора на последние цифры делимого и делителя
При использовании метода подбора частного для деления на двузначное число, может потребоваться перебрать несколько вариантов, прежде чем найти верное частное. Однако есть полезный прием, позволяющий сузить варианты и сделать меньше попыток. Этот прием основан на анализе последних цифр в записи делимого и делителя. Рассмотрим на примере деление 88 на 11. Последняя цифра в записи делимого - 8. Последняя цифра делителя - 1.
Для нахождения приблизительного частного посмотрим в таблицу умножения на 1. Какое число в этой таблице оканчивается на 8? Это число 8. Значит, в качестве пробного частного возьмем 8. Выполним проверку: 11 • 8 = 88 Частное найдено с первой попытки! Благодаря анализу последних цифр, мы сразу нашли верный результат, не перебирая лишних вариантов.
Этот прием также можно применить в случае деления 87 на 29: Последняя цифра делимого - 7. Последняя цифра делителя - 9. В таблице умножения на 9 находим число 21 (оно оканчивается на 7). Чтобы получить 21, нужно 9 умножить на 3. Значит, пробуем частное 3: 29 • 3 = 87 Частное верно!
Обобщим применение этого полезного приема в виде алгоритма:
- Записываем делимое и делитель
- Определяем их последние цифры
- В таблице умножения на последнюю цифру делителя находим число, оканчивающееся на последнюю цифру делимого
- Число, на которое нужно умножить делитель, чтобы получить это число, берем в качестве пробного частного
- Проверяем, перемножая делитель и предполагаемое частное
Таким образом, данный прием позволяет существенно упростить нахождение частного при делении на двузначное число за счет уменьшения перебора вариантов. Но в любом случае необходима проверка предполагаемого результата умножением. Этот метод опоры на последние цифры очень эффективен на практике.
Он сильно облегчает выполнение таких, казалось бы, сложных вычислений, как деление на двузначное число. Поэтому он часто используется в повседневных расчетах - при подсчете стоимости покупок в магазине, распределении расходов между людьми, вычислении объемов работ и многих других ситуациях.
Тренировочные упражнения по делению на двузначное число
Для закрепления навыка деления на двузначное число необходима регулярная тренировка с большим количеством практических упражнений. Рассмотрим несколько видов полезных заданий.
1. Заполнение пропусков Нужно вписать верное частное или пропущенный фрагмент проверки: 54 : __ = 2, так как 27 • 2 = __ 64 : 16 = __ 38 : 19 ≠ __, потому что 19 • __ = 63 Выполняя такие упражнения, нужно применять весь алгоритм деления с подбором, проверкой и фиксацией ошибок. Это помогает закрепить его отработку.
2. Исправление ошибок Дан ряд примеров на деление, в которых допущена 1 ошибка. Необходимо найти и исправить ее: 99 : 11 = 9 42 : 14 = 3 81 : 27 = 2 66 : 22 = 4 Решая подобные задания, нужно быть особенно внимательным, чтобы заметить единственную ошибку среди верных записей. Это развивает концентрацию и точность вычислений.
3. Расшифровка слов По результатам деления, записанным в виде кода, нужно восстановить заданное слово. Например: 78 : 26 = А 99 : 33 = С 78 : 13 = И 64 : 16 = Д 84 : 12 = О 70 : 14 = Л 88 : 11 = Е Ответ: СОСНА Такие упражнения одновременно тренируют вычислительные навыки и развивают логическое мышление.
4. Текстовые задачи Решение задач на деление в текстовой форме. Например: Для пошива платья требуется 248 см ткани. В магазин привезли рулоны ткани по 62 см в каждом. Сколько рулонов необходимо купить? Решение таких заданий позволяет отработать применение деления в реальных ситуациях.
5. Геометрические задачи Пример: Квадрат со стороной 33 см нужно разрезать на квадраты со стороной 11 см. Сколько получится маленьких квадратов? Решение подобных задач демонстрирует связь деления с геометрией.
6. Логические задачи Например: При делении числа 144 на некоторое двузначное число получилось в частном 18. Чему равен делитель? Решение логических задач требует особенно тщательных рассуждений, опирающихся на понимание свойств деления.
7. Практические задания Можно предложить следующие расчеты: Рассчитать стоимость 12 кг конфет по цене 34 руб/кг. Разложить 132 ореха поровну в 3 коробки. Узнать, во сколько раз выше забор, если его высота 66 см, а высота ворот 22 см. Такие задания закрепляют умение использовать деление в повседневной жизни.
Для эффективных тренировок желательно включать все разнообразие перечисленных упражнений. Это позволит комплексно отрабатывать вычислительные навыки, логическое мышление, умение решать задачи. В результате деление на двузначное число будет даваться легко и не вызовет трудностей на практике.



























