Биссектриса угла треугольника - важный элемент геометрии. Она делит угол пополам и соединяет вершину угла с серединой противоположной стороны. Биссектриса обладает удивительными свойствами, позволяющими решать множество геометрических задач. В этой статье мы подробно разберем, что такое биссектриса, ее определение и основные свойства. Рассмотрим также примеры применения биссектрисы при решении задач.
Определение и построение биссектрисы угла треугольника
Биссектриса угла треугольника - это луч, исходящий из вершины угла и делящий его пополам. Биссектриса соединяет вершину угла с противоположной стороной треугольника. Для построения биссектрисы нужно:
1. Построить угол треугольника и провести дугу окружности из вершины угла так, чтобы она пересекла обе стороны.
2. Соединить точки пересечения дуги со сторонами угла. Полученный отрезок и будет биссектрисой.
Каждый угол треугольника имеет свою биссектрису. Следовательно, в треугольнике можно построить три биссектрисы, по одной для каждого угла. Обозначают биссектрису через две буквы: первая - вершина угла, вторая - точка пересечения биссектрисы с противоположной стороной.
Биссектриса является важным элементом треугольника. Она позволяет решать многие задачи, опираясь на ее свойства. Правильное построение биссектрисы - залог верного решения.
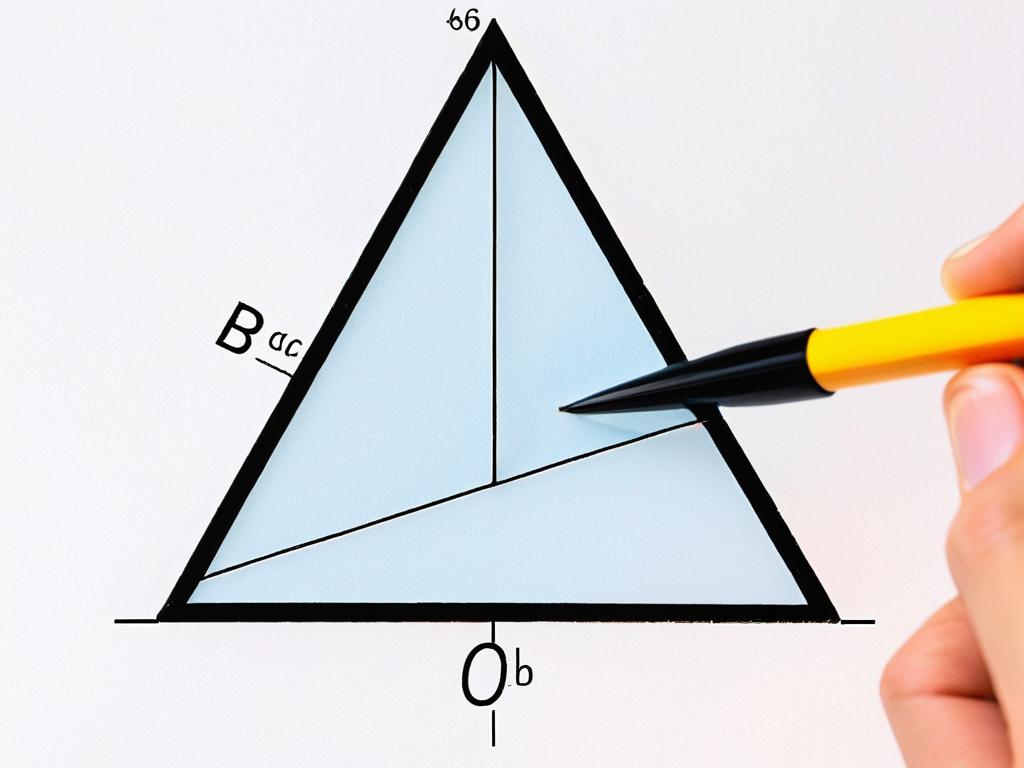
Основные свойства биссектрисы угла треугольника
Биссектриса угла треугольника обладает рядом важных свойств, которые широко применяются при решении геометрических задач. Рассмотрим основные из них:
- Биссектриса делит противоположную сторону треугольника на два отрезка, пропорциональных прилежащим сторонам. Это означает, что если биссектриса BD делит сторону AC на отрезки AD и DC, то отношение длин этих отрезков равно отношению длин сторон AB и BC: AD/DC = AB/BC.
- Биссектрисы пересекаются в одной точке, которая является центром окружности, вписанной в треугольник. Это важное свойство позволяет находить центр вписанной окружности, не прибегая к построениям.
- Все точки биссектрисы равноудалены от сторон того угла треугольника, из которого эта биссектриса выходит. Например, все точки биссектрисы BD равноудалены от сторон AB и AC угла BAC.
- Внешняя и внутренняя биссектрисы одного и того же угла треугольника перпендикулярны. Это свойство позволяет с помощью биссектрис строить перпендикуляр к стороне треугольника.
Зная эти свойства биссектрисы угла треугольника, можно решать множество задач на доказательство, вычисление, построение. Например, используя первое свойство, можно найти соотношение сторон треугольника, если известно деление биссектрисой противоположной стороны. По второму свойству определяется центр окружности, вписанной в треугольник. Третье свойство позволяет доказать, что точка лежит на биссектрисе угла. Четвертое - построить перпендикуляр к стороне треугольника.
Следующие два свойства биссектрисы не так широко используются на практике, но тоже важны:
- Длина биссектрисы угла треугольника выражается через стороны треугольника по формуле: AD^2 = ABAC - BDDC, где AD - биссектриса угла BAC, BD и DC - отрезки на стороне AC, на которые ее делит биссектриса.
- Биссектрисы, выходящие из одной вершины треугольника, делятся в этой вершине в отношении, равном сумме сторон, прилежащих к соответствующим углам, деленной на противоположную сторону.
Таким образом, биссектриса угла треугольника - это не просто линия, делящая угол пополам. Это мощный геометрический инструмент, позволяющий решать широкий круг задач благодаря своим замечательным свойствам.
Запомнив эти свойства и научившись их применять, можно существенно расширить свои возможности в плане решения разнообразных геометрических задач, связанных с треугольниками. Биссектриса угла треугольника - это не просто линия, делящая угол пополам. Это мощный геометрический инструмент, позволяющий решать широкий круг задач благодаря своим замечательным свойствам.
Примеры применения свойств биссектрисы при решении задач
Рассмотрим несколько примеров, демонстрирующих применение свойств биссектрисы угла треугольника при решении геометрических задач.
Задача 1. В треугольнике ABC биссектриса BD делит сторону AC на отрезки AD = 5 см и DC = 10 см. Найдите сторону AB, если BC = 12 см.
Решение. Используем свойство биссектрисы о пропорциональном делении противоположной стороны: AD/DC = AB/BC Подставляя числовые значения, получаем: 5/10 = AB/12 AB = 6 см
Задача 2. В треугольнике ABC угол A равен 50 градусов. Найдите угол B, если биссектрисы углов B и C пересекаются под углом 75 градусов.
Решение. По свойству биссектрис о пересечении в центре окружности, вписанной в треугольник, угол BOC равен разности углов B и C. Из условия имеем: BOC = 75 градусов. Так как сумма всех углов треугольника равна 180 градусов, то: A + B + C = 180 50 + B + C = 180 B + C = 180 - 50 = 130 Тогда угол B равен: B = 130 - 75 = 55 градусов
Задача 3. Дан треугольник ABC. Докажите, что точка K лежит на биссектрисе угла BAC, если KC = 5 см, KB = 4 см, AB = 6 см.
Решение. Воспользуемся свойством биссектрисы о равноудаленности ее точек от сторон угла: KC = KB (по условию) Значит, точка K равноудалена от сторон AB и AC. Следовательно, точка K лежит на биссектрисе угла BAC.
Задача 4. Постройте биссектрису угла B треугольника ABC, если AB = AC и ∠BAC = 70°. Найдите расстояние от вершины A до биссектрисы BD.
Решение. Так как AB = AC и ∠BAC = 70°, треугольник ABC - равнобедренный. Значит, биссектриса BD совпадает с медианой и высотой, проведенными к основанию BC. Строим биссектрису BD:
Треугольник ABD - равнобедренный, значит AD = AB. По условию AB = AC. Следовательно, искомое расстояние от точки A до биссектрисы равно: AD = AB = AC
Задача 5. На стороне AC треугольника ABC взята точка K так, что AK:KC = 1:3. Докажите, что AK - биссектриса угла BAC.
Решение. Проведем в треугольнике ABC биссектрису AD угла BAC. Тогда по свойству биссектрисы: AK/KD = AB/BC По условию задачи: AK/KC = 1/3 Но KD = KC, поскольку D и C лежат на одной прямой. Следовательно: AK/KD = AK/KC = 1/3 = AB/BC Значит, отрезок AK делит сторону AC в том же отношении, что и биссектриса AD, то есть совпадает с ней. Таким образом, AK - биссектриса угла BAC.
Эти примеры показывают, как можно использовать свойства биссектрисы угла треугольника при решении разнообразных задач. Зная эти свойства, можно определять элементы треугольника, проводить доказательные рассуждения, выполнять построения. Биссектриса - мощный инструмент геометрии, помогающий раскрывать ее красоту и гармонию.
Биссектриса - важный инструмент в геометрии треугольника
Биссектриса угла треугольника - это отрезок, соединяющий вершину угла с точкой на противоположной стороне и делящий угол пополам. Биссектриса обладает важными свойствами, позволяющими решать многие задачи на построение и вычисление в треугольнике.
Одним из важнейших свойств биссектрисы является то, что она делит противоположную сторону на отрезки, пропорциональные прилежащим сторонам. Это позволяет находить соотношения между сторонами треугольника, не зная его углов. Кроме того, точка пересечения биссектрис является центром окружности, вписанной в треугольник. Зная положение этой точки, можно строить многие линии в треугольнике, например медианы или высоты.
Еще одно полезное свойство биссектрисы - расстояние от любой ее точки до сторон угла одинаково. Это позволяет находить на биссектрисе точки, равноудаленные от заданных объектов. А зная длину биссектрисы и точки ее пересечения со сторонами, можно вычислить стороны и другие элементы треугольника.


























