Четырехугольник - один из основных объектов планиметрии. Изучение его свойств позволяет решать многие задачи геометрии. Особый интерес представляют углы четырехугольника, их соотношения и формулы. В этой статье мы подробно разберем основные свойства углов выпуклого четырехугольника, рассмотрим основные виды четырехугольников, выведем полезные формулы.
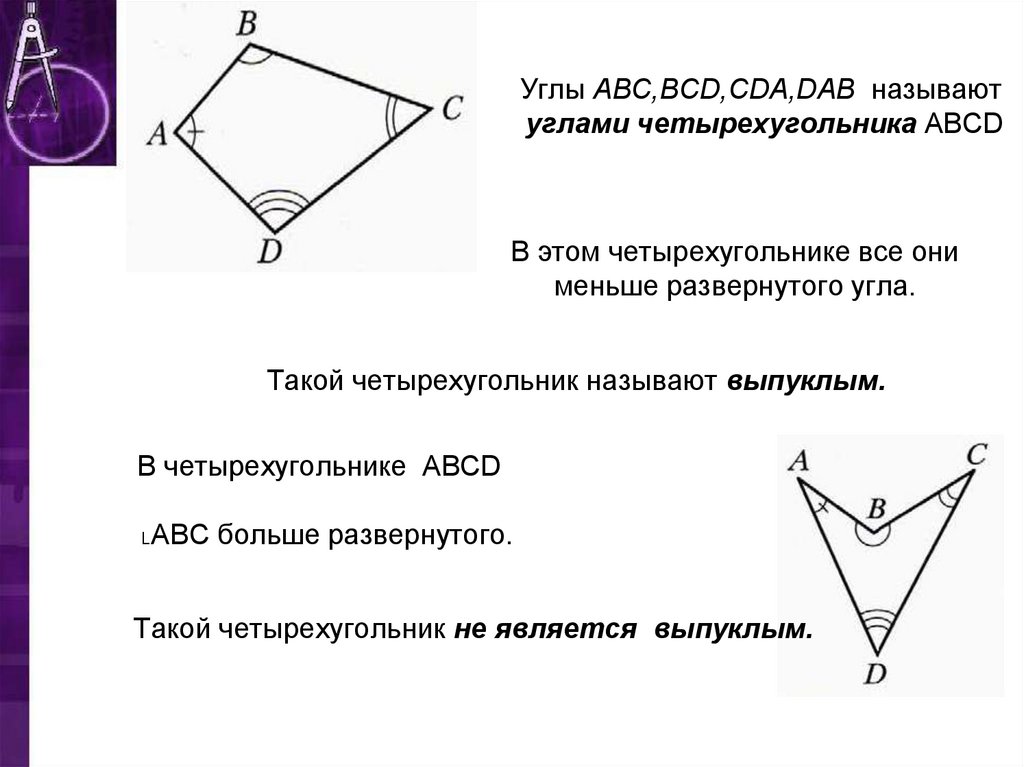
Основные определения и понятия
Четырехугольник – это геометрическая фигура, образованная четырьмя точками, которые соединены отрезками. Четырехугольник имеет четыре стороны и четыре угла. Углы четырехугольника делятся на внутренние и внешние. Сумма всех внутренних углов четырехугольника равна 360°. Четырехугольник называется выпуклым, если из любой его внутренней точки можно провести отрезок к любой стороне четырехугольника так, что он полностью лежит внутри фигуры.
Углы выпуклого четырехугольника обладают определенными свойствами. Рассмотрим некоторые из них.
- углы выпуклого четырехугольника
- углы четырехугольника
Далее мы подробно рассмотрим свойства углов выпуклого четырехугольника и соотношения между ними.
Свойства углов выпуклого четырехугольника
Углы выпуклого четырехугольника обладают следующими свойствами: сумма всех углов равна 360 градусов; каждый внутренний угол меньше суммы двух других внутренних углов.
Рассмотрим соотношения между углами выпуклого четырехугольника более подробно.
- Если диагонали четырехугольника перпендикулярны, то его противоположные углы равны.
- Если диагонали четырехугольника равны, то его противоположные углы равны.
Соотношения между углами четырехугольника
В любом выпуклом четырехугольнике существуют определенные соотношения между его углами. Рассмотрим некоторые из них.
- Сумма всех углов выпуклого четырехугольника равна 360°.
- Противолежащие углы выпуклого четырехугольника равны.
- Сумма соседних углов выпуклого четырехугольника равна 180°.
Кроме того, в некоторых частных случаях могут иметь место дополнительные соотношения между углами.
| Тип четырехугольника | Дополнительные соотношения между углами |
| Параллелограмм | Противолежащие углы равны |
| Прямоугольник | Все углы прямые |
| Ромб | Противолежащие углы равны, все углы равны |
| Квадрат | Все углы прямые и равны |
Таким образом, зная тип четырехугольника и некоторые его углы, можно определить остальные, используя соответствующие соотношения.
Формулы, связывающие углы и стороны
Между элементами выпуклого четырехугольника - его углами и сторонами - существует ряд зависимостей, которые можно выразить формулами. Рассмотрим четырехугольник ABCD. Обозначим длины его сторон через a, b, c и d, а величины углов через α, β, γ и δ. Тогда можно записать следующие формулы:
- a2 + b2 = c2 + d2 - 2cd cosα
- b2 + c2 = a2 + d2 - 2ad cosβ
- c2 + d2 = a2 + b2 - 2ab cosγ
- d2 + a2 = b2 + c2 - 2bc cosδ
Эти формулы выражают теорему косинусов для четырехугольника. Они позволяют вычислить одну сторону четырехугольника, если известны три другие стороны и угол между ними. Кроме того, существуют формулы, связывающие стороны четырехугольника с его диагоналями d1 и d2:
- d1 = √(a2 + c2 - 2ac cosα)
- d2 = √(b2 + d2 - 2bd cosγ)
А также формулы, выражающие синусы и косинусы углов четырехугольника через его стороны:
- sinα = (b2 + c2 - a2)/2bc
- cosα = (b2 + c2 - d2)/2bc
- sinβ = (a2 + d2 - c2)/2ad
- cosβ = (a2 + d2 - b2)/2ad
Используя эти формулы, можно установить множество зависимостей между элементами выпуклого четырехугольника, решая разнообразные задачи геометрии.





















