Как найти площадь прямоугольного треугольника необычным способом

На уроках геометрии в средней школе всем нам говорили о том, как найти площадь прямоугольного треугольника. Однако в рамках школьной программы мы получаем только самые необходимые знания и учимся наиболее распространенным и стандартным способам вычислений. Существуют ли необычные способы нахождения этой величины?

В качестве введения вспомним, какой треугольник считается прямоугольным, а также обозначим понятие площади.

Прямоугольным треугольником называют замкнутую геометрическую фигуру, один из углов которой равен 90⁰. Неотъемлемыми понятиями в определении прямоугольного треугольника являются катеты и гипотенуза. Под катетами подразумевают две стороны, которые в точке соединения образуют прямой угол. Гипотенуза – сторона, противоположная прямому углу. Прямой треугольник может быть равнобедренным (две его стороны будут иметь одинаковую величину), но никогда не будет равносторонним (все стороны одной длины). Определения высоты, медианы, векторов и прочих математических терминов подробно разбирать не будем. Их легко найти в справочниках.

Площадь прямого треугольника. В отличие от прямоугольников, правило о

произведении сторон в определении площади треугольника не действует. Если говорить сухим языком терминов, то под площадью треугольника понимают свойство этой фигуры занимать часть плоскости, выраженное числом. Довольно сложно к восприятию, согласитесь. Не будем пытаться глубоко вникнуть в определение, наша цель не в этом. Перейдем к главному – как найти площадь прямоугольного треугольника? Сами вычисления производить не будем, укажем только формулы. Для этого определимся с обозначениями: A,B,C – стороны треугольника, катеты – AB, BC. Угол ACB – прямой. S – площадь треугольника, h_nn – высота треугольника, где nn – сторона, на которую она опущена.

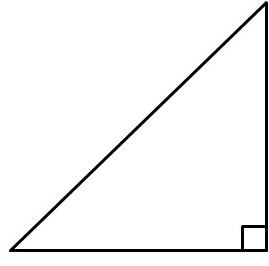
Способ 1. Как найти площадь прямоугольного треугольника, если известна величина его катетов

S= 0.5*a*b

Способ 2. Находим площадь равнобедренного прямоугольного треугольника

S= 0.5*h_BC*BC

Способ 3. Вычисление площади через прямоугольник

Достраиваем прямоугольный треугольник до квадрата (если треугольник

равнобедренный) или прямоугольника. Получим простой четырехугольник, составленный из 2-х идентичных прямоугольных треугольников. В этом случае значение площади одного из них будет равно половине площади полученной фигуры. S прямоугольника вычисляем произведением сторон. Обозначим эту величину M. Искомое значение площади будет равно половине M.

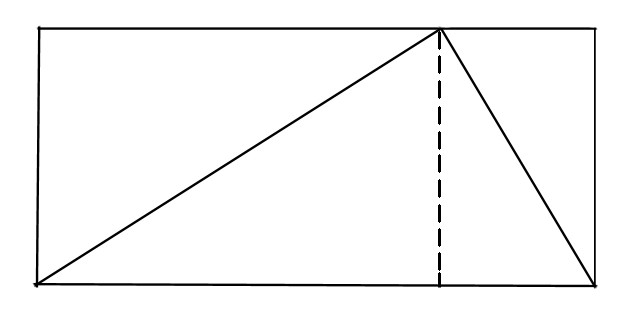
S=0.5*M

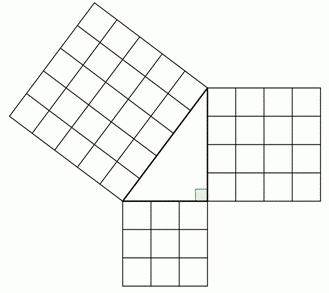
Способ 4. «Пифагоровы штаны». Знаменитая теорема Пифагора

Мы все помним ее формулировку: «сумма квадратов катетов...». Но не все могут

сказать, причем тут некие «штаны». Дело в том, что изначально Пифагор изучал взаимосвязь площадей квадратов, построенных на сторонах прямого треугольника. Выявив закономерности в соотношении сторон квадратов, он смог вывести и известную всем нам формулу. Ее можно применять в случае, когда неизвестна величина одной из сторон.

Способ 5. Как найти площадь прямоугольного треугольника по формуле Герона

Тоже достаточно простой способ расчета. Формула предполагает выражение площади треугольника через числовые значения его сторон. Для расчетов необходимо знать величины всех сторон треугольника.

S = (p–AC)*(p–BC), где p = (AB+BC+AC)*0.5

Кроме приведенных, существует множество других способов найти величину такой загадочной фигуры, как треугольник. Среди них: вычисление методом вписанной или описанной окружности, вычисление при помощи координат вершин, использование векторов, абсолютной величины, синусов, тангенсов.