Парабола - одна из самых распространенных кривых в математике и технике. Она встречается в оптике, строительстве, дизайне и других областях. Умение быстро находить ее вершину часто бывает ключевым для решения многих задач из разных сфер деятельности.
Основные понятия
Парабола - это геометрическое место точек на плоскости, равноудаленных от заданной точки F (фокус) и заданной прямой l (директриса). Формальное определение: Параболой называется множество всех точек плоскости, равноудаленных от данной точки F (фокус) и данной прямой l (директриса). Расстояние любой точки параболы до фокуса F равно ее расстоянию до директрисы l.
Основными элементами параболы являются:
- Директриса
- Фокус
- Вершина
Вершина параболы — точка пересечения ее оси симметрии с самой кривой. Это самая близкая к директрисе точка из всех точек параболы. Расстояние от нее до фокуса в 2 раза больше, чем до директрисы.
Методы нахождения вершины параболы
Существует несколько основных методов, позволяющих найти координаты вершины параболы:
- По формуле через коэффициенты квадратичной функции
- Методом выделения полного квадрата
- Через производную функции
Рассмотрим каждый подробнее.
Метод 1. Формула через коэффициенты функции

Координаты ее вершины можно найти по формулам:
x0 = -b / 2a
y0 = a*x02 + b*x0 + c
Где:
- x0, y0 - координаты вершины параболы
- a, b, c — коэффициенты заданной квадратичной функции
Это наиболее простой и быстрый способ. Основная формула для нахождения абсциссы вершины хорошо запоминается:
x0 = минус b деленное на 2a
Метод 2. Через выделение полного квадрата
Этот метод заключается в представлении квадратичной функции в виде полного квадрата суммы двух одночленов.
Например, функция y = x2 + 6x + 9 преобразуется следующим образом:
1) Группируем одночлены:
y = x2 + 6x + 9
2) Выносим общий множитель перед скобками:
y = (x + 3)2
Полученная функция имеет вид полного квадрата суммы одночленов. Вершиной такой параболы будет точка с координатами (-3; 9).
Абсцисса вершины всегда равна противоположному коэффициенту при x в исходном уравнении, взятому с противоположным знаком.
Метод 3. Через производную функции
Координаты вершины параболы можно найти и с помощью производной функции. Алгоритм следующий:
- Находим производную заданной квадратичной функции
- Приравниваем производную к 0 и решаем полученное уравнение относительно х
- Подставляем найденный х в исходную функцию и находим соответствующее значение y
Точка с координатами (х; у) и есть искомая вершина параболы.
Этот метод более трудоемкий, но позволяет отработать важные математические навыки.
Построение графика параболы
После того как координаты вершины параболы найдены, часто требуется построить график самой кривой. Для этого можно воспользоваться следующим алгоритмом:
- Задать значения аргумента x (например, от -5 до 5 с шагом 1)
- Подставить эти значения в уравнение параболы и найти соответствующие значения функции y
- Занести пары полученных значений (x;y) в таблицу
- По этим данным построить график в прямоугольной системе координат
- Отметить на графике точку ранее найденной вершины
Рассмотрим численный пример для функции из предыдущего раздела:
y = x2 - 2x - 3
Мы уже нашли, что ее вершина имеет координаты (1; -4). Построим теперь весь график:
| x | -2 | -1 | 0 | 1 | 0 | -1 | -2 |
| y | 5 | 0 | -3 | -4 | -3 | 0 | 5 |
По полученным данным строим график параболы:
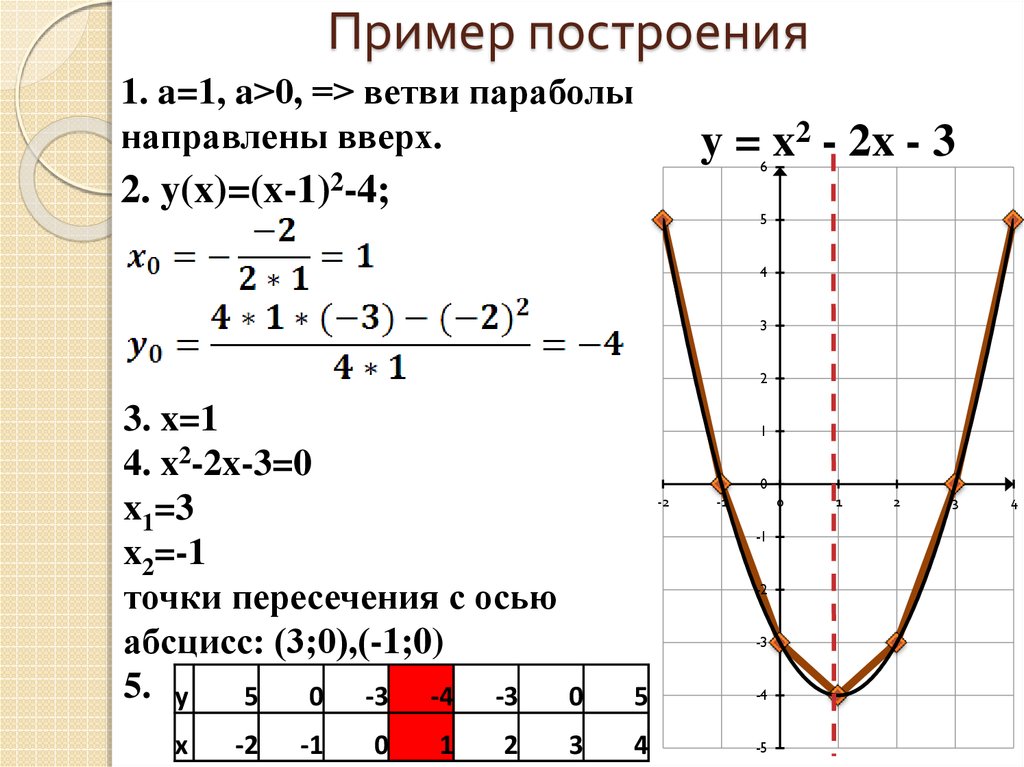
Как видно из рисунка, в точке с координатами (1; 3) действительно расположена вершина построенной параболы.
Рекомендации по оптимизации вычислений
Чтобы упростить процесс нахождения координат вершины и построения графика параболы, можно воспользоваться следующими советами:
- При задании функции вида y = ax2 брать значения x симметрично относительно нуля (например, -2 и 2, -3 и 3), это сократит объем вычислений
- Для построения графика достаточно 5-7 точек, слишком большое их количество усложняет работу
- Можно воспользоваться онлайн-калькуляторами или программами для визуализации парабол, чтобы сэкономить время на ручных расчетах
Однако на начальном этапе крайне важно отточить навыки по нахождению вершины параболы вручную, без использования вспомогательных инструментов. Только так можно в совершенстве овладеть всеми тонкостями работы с параболой как одним из ключевых объектов изучения в математике.