Чтобы в общих чертах представить себе, что такое окружность, взгляните на кольцо или обруч. Можно также взять круглый стакан и чашку, поставить вверх дном на лист бумаги и обвести карандашом. При многократном увеличении полученная линия станет толстой и не совсем ровной, и края ее будут размытыми. Окружность как геометрическая фигура не имеет такой характеристики, как толщина.
 Окружность: определение и основные средства описания
Окружность: определение и основные средства описания

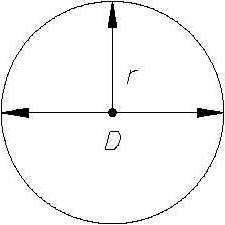
Окружность – это замкнутая кривая, состоящая из множества точек, расположенных в одной плоскости и равноудаленных от центра окружности. При этом центр находится в той же плоскости. Как правило, он обозначается буквой О.
Расстояние от любой из точек окружности до центра называется радиусом и обозначается буквой R.
Если соединить две любые точки окружности, то полученный отрезок будет называться хордой. Хорда, проходящая через центр окружности, - это диаметр, обозначаемый буквой D. Диаметр делит окружность на две равные дуги и по длине вдвое превышает размер радиуса. Таким образом, D = 2R, или R = D/2.
Свойства хорд
- Если через две любые точки окружности провести хорду, а затем перпендикулярно последней – радиус или диаметр, то этот отрезок разобьет и хорду, и дугу, отсеченную ею, на две равные части. Верно и обратное утверждение: если радиус (диаметр) делит хорду пополам, то он перпендикулярен ей.
- Если в пределах одной и той же окружности провести две параллельные хорды, то дуги, отсеченные ними, а также заключенные между ними, будут равны.
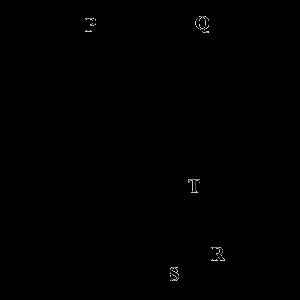
- Проведем две хорды PR и QS, пересекающиеся в пределах окружности в точке T. Произведение отрезков одной хорды всегда будет равно произведению отрезков другой хорды, то есть PT х TR = QT х TS.
Длина окружности: общее понятие и основные формулы
Одной из базовых характеристик данной геометрической фигуры является длина окружности. Формула выводится с использованием таких величин, как радиус, диаметр и константа "π", отражающая постоянство отношения длины окружности к ее диаметру.
Таким образом, L = πD, или L = 2πR, где L – это длина окружности, D – диаметр, R – радиус.
Формула длины окружности может рассматриваться как исходная при нахождении радиуса или диаметра по заданной длине окружности: D = L/π, R = L/2π.
Что такое окружность: основные постулаты
1. Прямая и окружность могут располагаться на плоскости следующим образом:
- не иметь общих точек;
- иметь одну общую точку, при этом прямая называется касательной: если провести радиус через центр и точку касания, то он будет перпендикулярен касательной;
- иметь две общие точки, при этом прямая называется секущей.
2. Через три произвольные точки, лежащие в одной плоскости, можно провести не более одной окружности.
3. Две окружности могут соприкасаться только в одной точке, которая расположена на отрезке, соединяющем центры этих окружностей.
4. При любых поворотах относительно центра окружность переходит сама в себя.
5. Что такое окружность с точки зрения симметрии?
- одинаковая кривизна линии в любой из точек;
- центральная симметрия относительно точки О;
- зеркальная симметрия относительно диаметра.
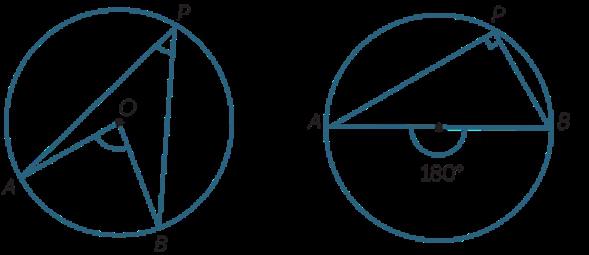
6. Если построить два произвольных вписанных угла, опирающихся на одну и ту же дугу окружности, они будут равны. Угол, опирающийся на дугу, равную половине длины окружности, то есть отсеченную хордой-диаметром, всегда равен 90°.
7. Если сравнивать замкнутые кривые линии одинаковой длины, то получится, что окружность отграничивает участок плоскости наибольшей площади.
Окружность, вписанная в треугольник и описанная около него
Представление о том, что такое окружность, будет неполным без описания особенностей взаимосвязи этой геометрической фигуры с треугольниками.
- При построении окружности, вписанной в треугольник, ее центр всегда будет совпадать с точкой пересечения биссектрис углов треугольника.
- Центр окружности, описанной около треугольника, располагается на пересечении срединных перпендикуляров к каждой из сторон треугольника.
- Если описать окружность около прямоугольного треугольника, то ее центр будет находиться на середине гипотенузы, то есть последняя будет являться диаметром.
- Центры вписанной и описанной окружностей будут находиться в одной точке, если базой для построения является равносторонний треугольник.
Основные утверждения об окружности и четырехугольниках
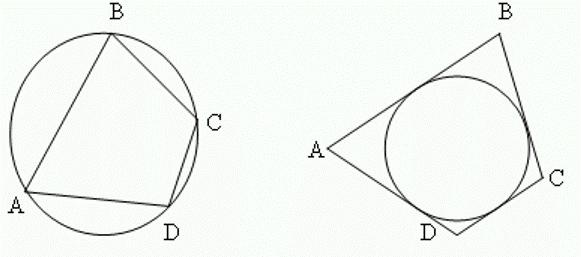
- Вокруг выпуклого четырехугольника можно описать окружность лишь тогда, когда сумма его противоположных внутренних углов равняется 180°.
- Построить вписанную в выпуклый четырехугольник окружность можно, если одинакова сумма длин его противоположных сторон.
- Описать окружность вокруг параллелограмма можно, если его углы прямые.
- Вписать в параллелограмм окружность можно в том случае, если все его стороны равны, то есть он является ромбом.
- Построить окружность через углы трапеции можно, только если она равнобедренная. При этом центр описанной окружности будет располагаться на пересечении оси симметрии четырехугольника и срединного перпендикуляра, проведенного к боковой стороне.

























