Длина окружности - один из важнейших параметров при решении многих практических задач, связанных с кругом и окружностью. Знание формул позволяет быстро и точно рассчитать это значение в нужных случаях.
Базовые понятия и определения
Прежде чем перейти непосредственно к формулам, давайте разберемся в некоторых базовых определениях.

Окружность и круг: в чем разница?
Окружность - это замкнутая кривая линия, состоящая из множества точек на одинаковом расстоянии от заданной точки (центра). Окружность ограничивает некую плоскую фигуру, которая называется кругом . Таким образом, можно сказать, что окружность - это граница круга.
Окружность нельзя "вырезать" из плоскости, в отличие от круга. Окружность - это абстрактное геометрическое понятие, математическая модель.
Радиус и диаметр
Любая точка на окружности находится от ее центра на фиксированном расстоянии, которое называется радиусом (обозначается буквой r). Это ключевой элемент окружности.
Другой важный элемент - диаметр (обозначается буквой d). Это отрезок, соединяющий две точки на окружности и проходящий через ее центр. Диаметр всегда в два раза больше радиуса:
d = 2*r
Зная значение радиуса или диаметра, можно вычислить длину окружности.

Формулы для вычисления длины окружности
Существует несколько основных формул, позволяющих найти длину окружности в зависимости от исходных данных. Рассмотрим их подробнее.
Через радиус
Если известен радиус окружности r, то длину окружности можно найти по формуле:
L = 2*π*r
Здесь L - искомая длина окружности, а π - математическая константа, равная примерно 3.14.
Например, радиус окружности равен 5 см. Тогда длина окружности составит:
L = 2*3.14*5 = 31.4 см
Через диаметр
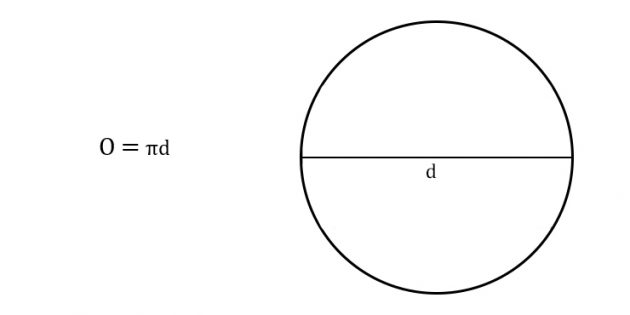
Если вместо радиуса известен диаметр d, то используется формула:
L = π*d
Поскольку d = 2*r, эта формула полностью эквивалентна предыдущей. Просто в ней сразу используется диаметр вместо удвоенного радиуса.
Например, диаметр окружности равен 10 см. Ее длина составит:
L = 3.14*10 = 31.4 см
Как видите, ответ совпадает с предыдущим примером, поскольку радиус там был равен 5 см (половина от диаметра 10 см).
Через площадь круга
Если известна площадь круга S, ограниченного окружностью, то длину окружности можно найти по формуле:
L = 2*(S/π)^(1/2)
Здесь нужно вычислить квадратный корень от частного площади круга и числа π. Это чуть более сложный вариант, по сравнению с предыдущими формулами.
Допустим, площадь круга равна 100 кв. см. Тогда:
L = 2*(100/3.14)^(1/2) = 2*10 = 20 см
Другие формулы вычисления
Помимо основных рассмотренных вариантов, длину окружности можно вычислить и через ряд других похожих формул. Рассмотрим некоторые из них.
С использованием вписанных фигур
Если окружность вписана в правильный многоугольник, известна его сторона a, то:
- Для квадрата:
L = 4*a - Для правильного шестиугольника:
L = 3*√3*a - Для правильного восьмиугольника:
L = 4*√2*a
Здесь длина окружности выражается через сторону вписанного многоугольника с использованием определенных коэффициентов.
С применением описанных фигур
Аналогично можно использовать параметры описанной вокруг окружности фигуры:
- Для квадрата:
L = π*a - Для правильного шестиугольника:
L = 3*a
Здесь в формулы вместо радиуса или диаметра подставляется сторона описанного многоугольника.
Используя хорды и касательные
Хордой называется отрезок, соединяющий две точки на окружности. При равных хордах можно записать:
L = 4*a
Где a - длина хорды.
А если воспользоваться касательными, то получаем:
L = 2*π*a
Здесь a - расстояние от центра окружности до точки касания.
Какую формула выбрать?
Итак, мы рассмотрели целый ряд различных формул для нахождения длины окружности. Какую же из них выбрать в конкретной ситуации?
Рекомендуется отдавать предпочтение более простым вариантам (L=2πr или L=πd) при наличии соответствующих исходных данных. А формулы через вспомогательные фигуры и параметры использовать только при отсутствии радиуса и диаметра.
























