Мир устроен так, что решение большого количества задач сводится к нахождению корней квадратного уравнения. Корни уравнений имеют важное значение для описания различных закономерностей. Это было известно еще землемерам древнего Вавилона. Астрономы и инженеры тоже были вынуждены решать такие задачи. Еще в VI веке нашей эры индийский ученый Ариабхата разработал основы нахождения корней квадратного уравнения. Формулы приобрели законченный вид в XIX веке.
Общие понятия
Предлагаем ознакомиться с основными закономерностями квадратичных равенств. В общем виде равенство может быть записано так:
ax2 + bx + c = 0,
Число корней квадратного уравнения может быть равно одному или двум. Быстрый анализ можно провести, используя понятие дискриминант:
D = b2 - 4ac
В зависимости от вычисленного значения получаем:
- При D > 0 существуют два различных корня. Формула в общем виде для определения корней квадратного уравнения выглядит как (-b± √D) / (2a).
- D = 0, в этом случае корень один и соответствует значению x = -b / (2a)
- D < 0, для отрицательного значения дискриминанта решения уравнения не существует.
Замечание: если дискриминант отрицательный, уравнение не имеет корней только в области вещественных чисел. Если алгебру расширить до понятия комплексных корней, то уравнение имеет решение.
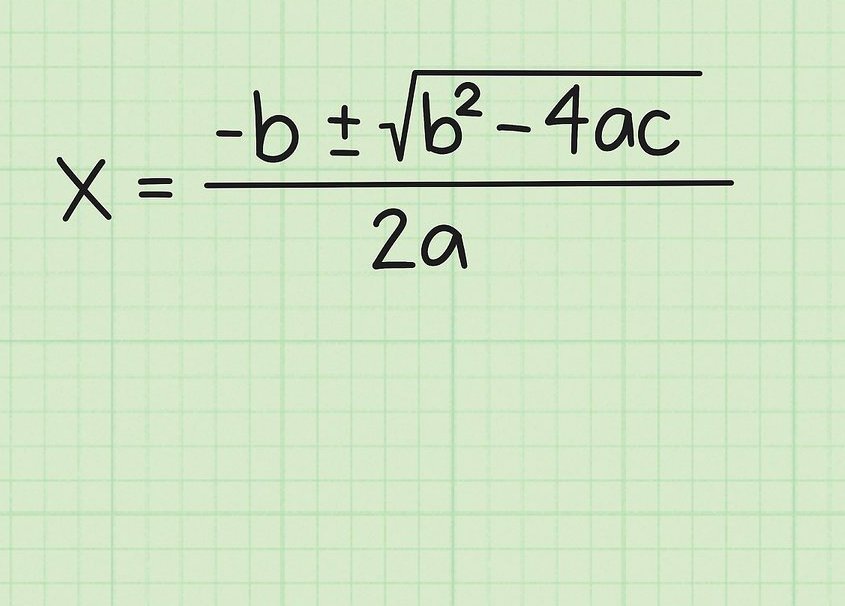
Приведем цепочку действий, подтверждающую формулу нахождения корней.
Из общего вида уравнения, следует:
ax2 + bx = -c
Правую и левую части умножаем на 4a и добавляем b2, получаем
4a2x2 + 4abx + b2 = -4ac+b2
Преобразуем левую часть в виде квадрата многочлена (2ax + b)2. Извлекаем квадратный корень из обеих частей уравнения 2ax + b= -b ± √(-4ac + b2), переносим коэффициент b в правую часть, получим:
2ax = -b ± √(-4ac + b2)
Отсюда следует:
x = (-b ± √(b2 - 4ac))
Что и требовалось показать.
Частный случай
В некоторых случаях решение задачи может упроститься. Так, при четном коэффициенте b получим более простую формулу.
Обозначим k = 1/2b, тогда формула общего вида корней квадратного уравнения принимает вид:
x = (-k ± √(k2 - ac)) / a
При D = 0, получаем x = -k / a
Другим частным случаем будет решение уравнения при a = 1.
Для вида x2 + bx + c = 0 корни будут x = -k ± √(k2 - c) при дискриминанте больше 0. Для случая когда D = 0, корень будет определяться простой формулой: x = -k.
Использование графиков
Любой человек, даже не подозревая этого, постоянно сталкивается с физическими, химическими, биологическими и даже социальными явлениями, которые хорошо описываются квадратичной функцией.
Замечание: кривая, построенная на основании квадратичной функции, получила название параболы.
Приведем несколько примеров.
- При расчете траектории полета снаряда используют свойство движения по параболе тела, выпущенного под углом к горизонту.
- Свойство параболы равномерно распределять нагрузку широко используется в архитектуре.

Понимая всю важность параболической функции, разберемся, как с помощью графика исследовать ее свойства, используя понятия "дискриминант" и "корни квадратного уравнения".
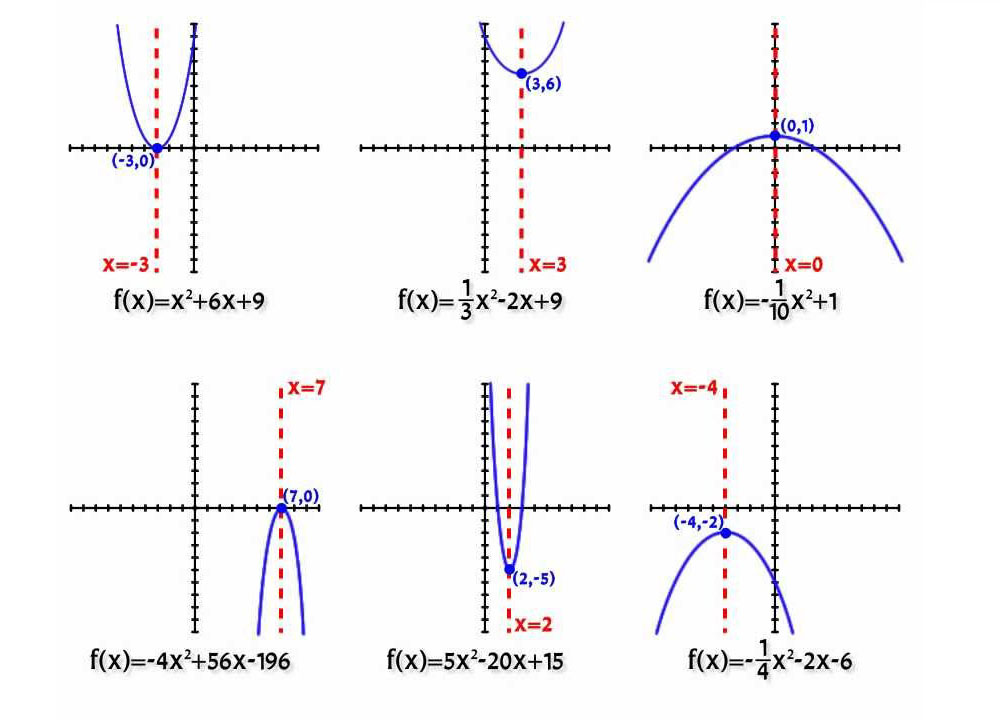
В зависимости от величины коэффициентов a и b, существует всего шесть вариантов положения кривой:
- Дискриминант положительный, a и b имеют разные знаки. Ветви параболы смотрят вверх, у квадратичного уравнения два решения.
- Дискриминант и коэффициент b равны нулю, коэффициент a больше нуля. График расположен в положительной зоне, уравнение имеет 1 корень.
- Дискриминант и все коэффициенты имеют положительные значения. У квадратичного уравнения нет решения.
- Дискриминант и коэффициент а - отрицательные, b - больше нуля. Ветви графика направлены вниз, у уравнения два корня.
- Дискриминант и коэффициент b равны нулю, коэффициент a - отрицательный. Парабола смотрит вниз, у уравнения один корень.
- Значения дискриминанта и всех коэффициентов - отрицательные. Решений нет, значения функции полностью в отрицательной зоне.
Замечание: вариант a = 0 не рассматривается, так как в этом случае парабола вырождается в прямую.
Все сказанное хорошо иллюстрирует рисунок, представленный ниже.
Примеры решения задач
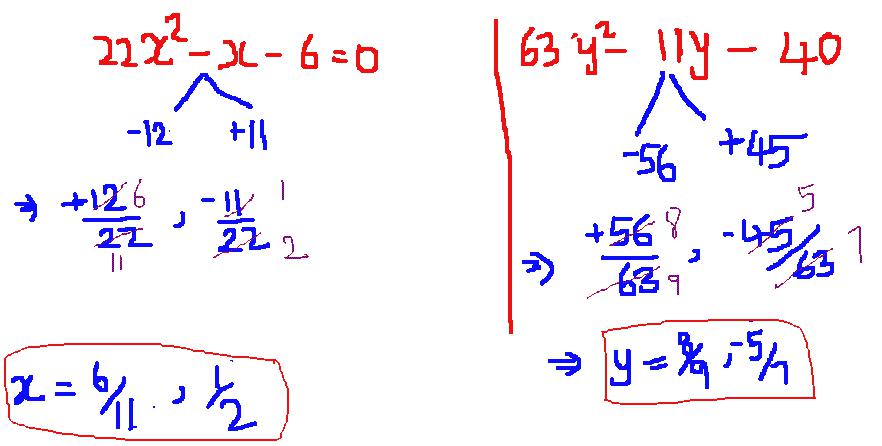
Условие: используя общие свойства, составьте квадратное уравнение, корни которого равны между собой.
Решение:
по условию задачи x1 = x2, или -b + √(b2 - 4ac) / (2a) = -b + √(b2 - 4ac) / (2a). Упрощаем запись:
-b + √(b2 - 4ac) / (2a) - (-b - √(b2 - 4ac) / (2a)) = 0, раскрываем скобки и приводим подобные члены. Уравнение принимает вид 2√(b2 - 4ac) = 0. Это утверждение верно, когда b2 - 4ac = 0, отсюда b2 = 4ac, тогда значение b = 2√(ac) подставляем в уравнение
ax2 + 2√(ac)x + c = 0, в приведенном виде получаем x2 + 2√(c / a)x + c = 0.
Ответ:
при a не равном 0 и любом c существует только одно решение, если b = 2√(c / a).
Квадратные уравнения при всей своей простоте имеют большое значение в инженерных расчетах. Практически любой физический процесс можно описать с некоторым приближением, используя степенные функции порядка n. Квадратное уравнение будет первым таким приближением.



























