В курсе средней и старшей школы учащиеся проходили тему «Дроби». Однако это понятие гораздо шире, чем дается в процессе обучения. Сегодня понятие дроби встречается достаточно часто, и не каждый может провести вычисления какого-либо выражения, к примеру, умножение дробей.
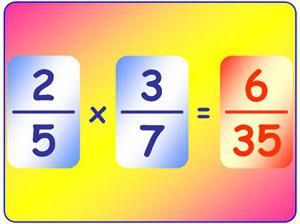
Что такое дробь?
Так исторически сложилось, что дробные числа появились из-за необходимости измерять. Как показывает практика, часто встречаются примеры на определение длины отрезка, объема прямоугольного параллелепипеда, площади прямоугольника.
Первоначально ученики знакомятся с таким понятием, как доля. К примеру, если разделить арбуз на 8 частей, то каждому достанется по одной восьмой арбуза. Вот эта одна часть из восьми и называется долей.
Доля, равная ½ от какой-либо величины, называется половиной; ⅓ - третью; ¼ - четвертью. Записи вида 5/8, 4/5, 2/4 называют обыкновенными дробями. Обыкновенная дробь разделяется на числитель и знаменатель. Между ними находится черта дроби, или дробная черта. Дробную черту можно нарисовать в виде как горизонтальной, так и наклонной линии. В данном случае она обозначает знак деления.
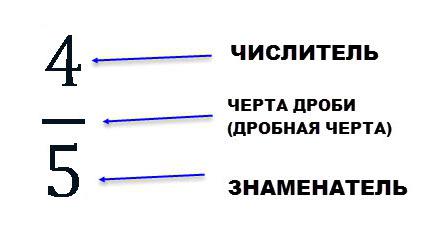
Знаменатель представляет, на сколько одинаковых долей разделяют величину, предмет; а числитель – сколько одинаковых долей взято. Числитель пишется над дробной чертой, знаменатель - под ней.
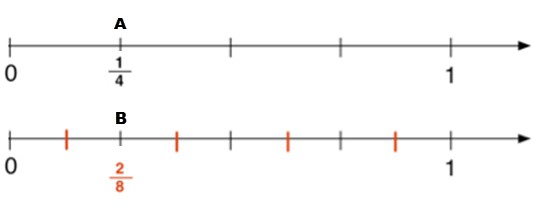
Удобнее всего показать обыкновенные дроби на координатном луче. Если единичный отрезок разделить на 4 равные доли, обозначить каждую долю латинской буквой, то в результате можно получить отличное наглядное пособие. Так, точка А показывает долю, равную 1/4 от всего единичного отрезка, а точка В отмечает 2/8 от данного отрезка.
Разновидности дробей
Дроби бывают обыкновенные, десятичные, а также смешанные числа. Кроме того, дроби можно разделить на правильные и неправильные. Эта классификация больше подходит для обыкновенных дробей.
Под правильной дробью понимают число, у которого числитель меньше знаменателя. Соответственно, неправильная дробь – число, у которого числитель больше знаменателя. Второй вид обычно записывают в виде смешанного числа. Такое выражение состоит из целой и дробной части. Например, 1½. 1 - целая часть, ½ - дробная. Однако если нужно провести какие-то манипуляции с выражением (деление или умножение дробей, их сокращение или преобразование), смешанное число переводится в неправильную дробь.
Правильное дробное выражение всегда меньше единицы, а неправильное – больше либо равно 1.
Что касается десятичных дробей, то под этим выражением понимают запись, в которой представлено любое число, знаменатель дробного выражения которого можно выразить через единицу с несколькими нулями. Если дробь правильная, то целая часть в десятичной записи будет равна нулю.
Чтобы записать десятичную дробь, нужно сначала написать целую часть, отделить ее от дробной с помощью запятой и потом уже записать дробное выражение. Необходимо помнить, что после запятой числитель должен содержать столько же цифровых символов, сколько нулей в знаменателе.
Пример. Представить дробь 721/1000 в десятичной записи.
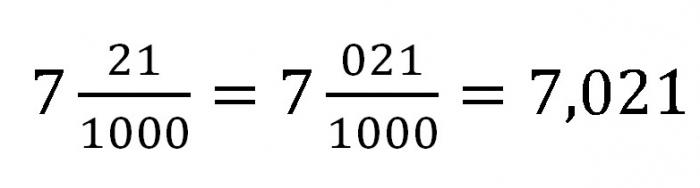
Алгоритм перевода неправильной дроби в смешанное число и наоборот
Записывать в ответе задачи неправильную дробь некорректно, поэтому ее нужно перевести в смешанное число:
- разделить числитель на имеющийся знаменатель;
- в конкретном примере неполное частное – целое;
- и остаток – числитель дробной части, причем знаменатель остается неизменным.
Пример. Перевести неправильную дробь в смешанное число: 47/5.
Решение. 47 : 5. Неполное частное равняется 9, остаток = 2. Значит, 47/5 = 92/5.
Иногда нужно представить смешанное число в качестве неправильной дроби. Тогда нужно воспользоваться следующим алгоритмом:
- целая часть умножается на знаменатель дробного выражения;
- полученное произведение прибавляется к числителю;
- результат записывается в числителе, знаменатель остается неизменным.
Пример. Представить число в смешанном виде в качестве неправильной дроби: 98/10.
Решение. 9 х 10 + 8 = 90 + 8 = 98 – числитель.
Ответ: 98/10.
Умножение дробей обыкновенных
Над обыкновенными дробями можно совершать различные алгебраические операции. Чтобы перемножить два числа, нужно числитель перемножить с числителем, а знаменатель со знаменателем. Причем умножение дробей с разными знаменателями не отличается от произведения дробных чисел с одинаковыми знаменателями.

Случается, что после нахождения результата нужно сократить дробь. В обязательном порядке нужно максимально упростить получившееся выражение. Конечно, нельзя сказать, что неправильная дробь в ответе – это ошибка, но и назвать верным ответом ее тоже затруднительно.
Пример. Найти произведение двух обыкновенных дробей: ½ и 20/18.
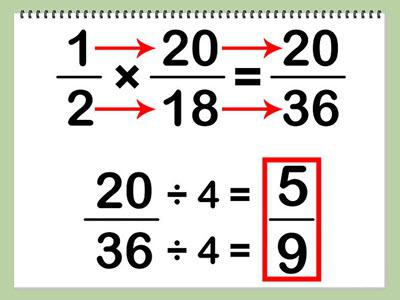
Как видно из примера, после нахождения произведения получилась сократимая дробная запись. И числитель, и знаменатель в данном случае делится на 4, и результатом выступает ответ 5/9.
Умножение дробей десятичных
Произведение десятичных дробей довольно сильно отличается от произведения обыкновенных по своему принципу. Итак, умножение дробей заключается в следующем:
- две десятичные дроби нужно записать друг под другом так, чтобы крайние правые цифры оказались одна под другой;
- нужно перемножить записанные числа, несмотря на запятые, то есть как натуральные;
- подсчитать количество цифр после знака запятой в каждом из чисел;
- в получившемся после перемножения результате нужно отсчитать справа столько цифровых символов, сколько содержится в сумме в обоих множителях после запятой, и поставить отделяющий знак;
- если цифр в произведении оказалось меньше, тогда перед ними нужно написать столько нулей, чтобы покрыть это количество, поставить запятую и приписать целую часть, равную нулю.

Пример. Вычислить произведение двух десятичных дробей: 2,25 и 3,6.
Решение.

Умножение смешанных дробей
Чтобы вычислить произведение двух смешанных дробей, нужно использовать правило умножения дробей:
- перевести числа в смешанном виде в неправильные дроби;
- найти произведение числителей;
- найти произведение знаменателей;
- записать получившийся результат;
- максимально упростить выражение.
Пример. Найти произведение 4½ и 62/5.

Умножение числа на дробь (дроби на число)
Помимо нахождения произведения двух дробей, смешанных чисел, встречаются задания, где нужно помножить натуральное число на дробь.
Итак, чтобы найти произведение десятичной дроби и натурального числа, нужно:
- записать число под дробью так, чтобы крайние правые цифры оказались одна над другой;
- найти произведение, несмотря на запятую;
- в полученном результате отделить целую часть от дробной с помощью запятой, отсчитав справа то количество знаков, которое находится после запятой в дроби.
Чтобы умножить обыкновенную дробь на число, следует найти произведение числителя и натурального множителя. Если в ответе получается сократимая дробь, ее следует преобразовать.
Пример. Вычислить произведение 5/8 и 12.
Решение. 5/8 * 12 = (5*12)/8 = 60/8 = 30/4 = 15/2 = 71/2.
Ответ: 71/2.
Как видно из предыдущего примера, необходимо было сократить получившийся результат и преобразовать неправильное дробное выражение в смешанное число.
Также умножение дробей касается и нахождения произведения числа в смешанном виде и натурального множителя. Чтобы перемножить эти два числа, следует целую часть смешанного множителя умножить на число, числитель помножить на это же значение, а знаменатель оставить неизменным. Если требуется, нужно максимально упростить получившийся результат.
Пример. Найти произведение 95/6 и 9.
Решение. 95/6 х 9 = 9 х 9 + (5 х 9)/6 = 81 + 45/6 = 81 + 73/6 = 881/2.
Ответ: 881/2.
Умножение на множители 10, 100, 1000 или 0,1; 0,01; 0,001
Из предыдущего пункта вытекает следующее правило. Для умножения дроби десятичной на 10, 100, 1000, 10000 и т. д. нужно передвинуть запятую вправо на столько символов цифр, сколько нулей во множителе после единицы.
Пример 1. Найти произведение 0,065 и 1000.
Решение. 0,065 х 1000 = 0065 = 65.
Ответ: 65.
Пример 2. Найти произведение 3,9 и 1000.
Решение. 3,9 х 1000 = 3,900 х 1000 = 3900.
Ответ: 3900.
Если нужно перемножить натуральное число и 0,1; 0,01; 0,001; 0,0001 и т. д., следует передвинуть влево запятую в получившемся произведении на столько символов цифр, сколько нулей находится до единицы. Если необходимо, перед натуральным числом записываются нули в достаточном количестве.
Пример 1. Найти произведение 56 и 0,01.
Решение. 56 х 0,01 = 0056 = 0,56.
Ответ: 0,56.
Пример 2. Найти произведение 4 и 0,001.
Решение. 4 х 0,001 = 0004 = 0,004.
Ответ: 0,004.
Итак, нахождение произведения различных дробей не должно вызывать затруднений, разве что подсчет результата; в таком случае без калькулятора просто не обойтись.


























