Из множества геометрических фигур одной из самых простых можно назвать параллелепипед. Он имеет форму призмы, в основании которой расположен параллелограмм. Не составляет труда подсчитать площадь параллелепипеда, поскольку формула очень проста.
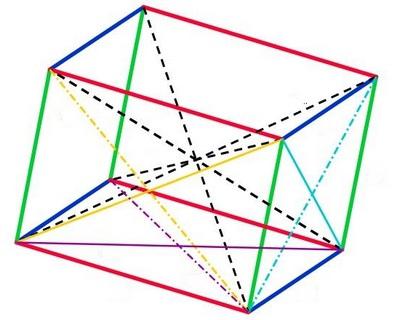
Параллелепипед (в переводе с греческого языка термин означает «параллельные грани») обладает некоторыми свойствами, которые следует упомянуть. Во-первых, симметричность фигуры подтверждается только в середине каждой своей диагонали. Во-вторых, проведя между любыми из противоположных вершин диагональ, можно обнаружить, что все вершины имеют единую точку пересечения. Также стоит отметить то свойство, что противоположные грани всегда равны и будут обязательно параллельны между собой.
В природе различают такие разновидности параллелепипедов:
прямоугольный - состоит из граней прямоугольной формы;
прямой - имеет только боковые грани прямоугольные;
наклонный параллелепипед имеет в составе боковые грани, которые поставлены неперпендикулярно основаниям;
куб - состоит из граней квадратной формы.
Попробуем найти площадь параллелепипеда на примере прямоугольного типа этой фигуры. Как нам уже известно, все его грани прямоугольные. И поскольку количество этих элементов сводится к шести, то, узнав площадь каждой грани, нужно суммировать получившиеся результаты в одно число. А найти площадь каждой из них не составит труда. Для этого необходимо умножить две стороны прямоугольника.
Используется математическая формула, чтобы определить площадь прямоугольного параллелепипеда. Она состоит из знаковых символов, обозначающих грани, площадь, и выглядит так: S=2(ab+bc+ac), где S – площадь фигуры, a, b — стороны основания, c — боковое ребро.
Приведём примерное вычисление. Допустим, a = 20 см, b = 16 см, c = 10 см. Теперь нужно перемножить числа в соответствии с требованиями формулы: 20*16+16*10+20*10 и получаем число 680 см2. Но это будет лишь половина фигуры, так как мы узнали и суммировали площади трёх граней. Поскольку каждая грань имеет своего «двойника», нужно удвоить результирующее значение, и получаем площадь параллелепипеда, равную 1360 см2.
Чтобы вычислить площадь боковой поверхности, применяют формулу S=2c(a+b). Площадь основания параллелепипеда можно узнать, умножая длины сторон основания друг на друга.

В повседневном быту параллелепипеды можно встретить часто. О их существовании нам напоминает форма кирпича, деревянного ящика письменного стола, обычного спичечного коробка. Примеров каждый сможет найти в изобилии вокруг нас. В школьных программах по геометрии на изучение параллелепипеда отведено несколько уроков. Первые из них демонстрируют модели прямоугольного параллелепипеда. Затем ученикам показывают, как вписывать в него шар или пирамиду, другие фигуры, находить площадь параллелепипеда. Одним словом, это простейшая трёхмерная фигура.





















