История тригонометрии неразрывно связана с астрономией, ведь именно для решения задач этой науки древние ученые стали исследовать соотношения различных величин в треугольнике.
На сегодняшний день тригонометрия является микроразделом математики, изучающим зависимость между значениями величин углов и длин сторон треугольников, а также занимающимся анализом алгебраических тождеств тригонометрических функций.
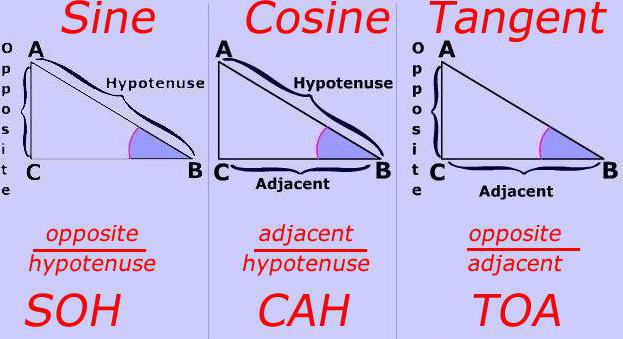
Термин «тригонометрия»
Сам термин, давший название этому разделу математики, впервые был обнаружен в заголовке книги под авторством немецкого ученого-математика Питискуса в 1505 году. Слово «тригонометрия» имеет греческое происхождение и означает «измеряю треугольник». Если быть точнее, то речь идет не о буквальном измерении этой фигуры, а об её решении, то есть определении значений её неизвестных элементов с помощью известных.
Общие сведения о тригонометрии
История тригонометрии началась более двух тысячелетий назад. Первоначально ее возникновение было связано с необходимостью выяснения соотношений углов и сторон треугольника. В процессе исследований выяснилось, что математическое выражение данных соотношений требует введения особых тригонометрических функций, которые первоначально оформлялись как числовые таблицы.
Для многих смежных с математикой наук толчком к развитию стала именно история тригонометрии. Происхождение единиц измерения углов (градусов), связанное с исследованиями ученых Древнего Вавилона, опирается на шестидесятиричную систему исчисления, которая дала начала современной десятиричной, применяемой во многих прикладных науках.
Предполагается, что изначально тригонометрия существовала как часть астрономии. Затем она стала использоваться в архитектуре. А со временем возникла целесообразность применения данной науки в различных областях человеческой деятельности. Это, в частности, астрономия, морская и воздушная навигация, акустика, оптика, электроника, архитектура и прочие.
Тригонометрия в ранние века
Руководствуясь данными о сохранившихся научных реликвиях, исследователи сделали вывод, что история возникновения тригонометрии связана с работами греческого астронома Гиппарха, который впервые задумался над поиском способов решения треугольников (сферических). Его труды относятся ко 2 веку до нашей эры.

История развития тригонометрии в Древней Греции связана с именем астронома Птоломея - автора геоцентрической системы мира, господствовавшей до Коперника.
Греческим астрономам не были известны синусы, косинусы и тангенсы. Они пользовались таблицами, позволяющими найти значение хорды окружности с помощью стягиваемой дуги. Единицами для измерения хорды были градусы, минуты и секунды. Один градус приравнивался к шестидесятой части радиуса.
Также исследования древних греков продвинули развитие сферической тригонометрии. В частности, Евклид в своих «Началах» приводит теорему о закономерностях соотношений объемов шаров различного диаметра. Его труды в этой области стали своеобразным толчком в развитии еще и смежных областей знаний. Это, в частности, технология астрономических приборов, теория картографических проекций, система небесных координат и т. д.

Средневековье: исследования индийских ученых
Значительных успехов достигли индийские средневековые астрономы. Гибель античной науки в IV веке обусловила перемещение центра развития математики в Индию.
История возникновения тригонометрии как обособленного раздела математического учения началась в Средневековье. Именно тогда ученые заменили хорды синусами. Это открытие позволило ввести функции, касающиеся исследования сторон и углов прямоугольного треугольника. То есть именно тогда тригонометрия начала обосабливаться от астрономии, превращаясь в раздел математики.
Первые таблицы синусов были у Ариабхаты, они была проведены через 3о, 4о, 5о. Позже появились подробные варианты таблиц: в частности, Бхаскара привел таблицу синусов через 1о.

История развития тригонометрии в Европе
После перевода арабских трактатов на латынь (XII-XIII в) большинство идей индийских и персидских ученых были заимствованы европейской наукой. Первые упоминания о тригонометрии в Европе относятся к XII веку.
По мнению исследователей, история тригонометрии в Европе связана с именем англичанина Ричарда Уоллингфордского, который стал автором сочинения «Четыре трактата о прямых и обращенных хордах». Именно его труд стал первой работой, которая целиком посвящена тригонометрии. К XV веку многие авторы в своих трудах упоминают о тригонометрических функциях.
История тригонометрии: Новое время
В Новое время большинство ученых стало осознавать чрезвычайную важность тригонометрии не только в астрономии и астрологии, но и в других областях жизни. Это, в первую очередь, артиллерия, оптика и навигация в дальних морских походах. Поэтому во второй половине XVI века эта тема заинтересовала многих выдающихся людей того времени, в том числе Николая Коперника, Иоганна Кеплера, Франсуа Виета. Коперник отвел тригонометрии несколько глав своего трактата «О вращении небесных сфер» (1543). Чуть позже, в 60-х годах XVI века, Ретик - ученик Коперника - приводит в своем труде «Оптическая часть астрономии» пятнадцатизначные тригонометрические таблицы.

Заслуги Леонарда Эйлера
Придание тригонометрии современного содержания и вида стало заслугой Леонарда Эйлера. Его трактат «Введение в анализ бесконечных» (1748) содержит определение термина «тригонометрические функции», которое эквивалентно современному. Таким образом, этот ученый смог определить обратные функции. Но и это еще не все.
Определение тригонометрических функций на всей числовой прямой стало возможным благодаря исследованиям Эйлера не только допустимых отрицательных углов, но и углов боле 360°. Именно он в своих работах впервые доказал, что косинус и тангенс прямого угла отрицательные. Разложение целых степеней косинуса и синуса тоже стало заслугой этого ученого. Общая теория тригонометрических рядов и изучение сходимости полученных рядов не были объектами исследований Эйлера. Однако, работая над решением смежных задач, он сделал много открытий в этой области. Именно благодаря его работам продолжилась история тригонометрии. Кратко в своих трудах он касался и вопросов сферической тригонометрии.

Области применения тригонометрии
Тригонометрия не относится к прикладным наукам, в реальной повседневной жизни ее задачи редко применяются. Однако этот факт не снижает ее значимости. Очень важна, например, техника триангуляции, которая позволяет астрономам достаточно точно измерить расстояние до недалеких звезд и осуществлять контроль за системами навигации спутников.
Также тригонометрию применяют в навигации, теории музыки, акустике, оптике, анализе финансовых рынков, электронике, теории вероятностей, статистике, биологии, медицине (например, в расшифровке ультразвуковых исследований УЗИ и компьютерной томографии), фармацевтике, химии, теории чисел, сейсмологиии, метеорологии, океанологии, картографии, многих разделах физики, топографии и геодезии, архитектуре, фонетике, экономике, электронной технике, машиностроении, компьютерной графике, кристаллографиии и т. д. История тригонометрии и ее роль в изучении естественно-математических наук изучаются и по сей день. Возможно, в будущем областей ее применения станет еще больше.
История происхождения основных понятий
История возникновения и развития тригонометрии насчитывает не один век. Введение понятий, которые составляют основу этого раздела математической науки, также не было одномоментным.
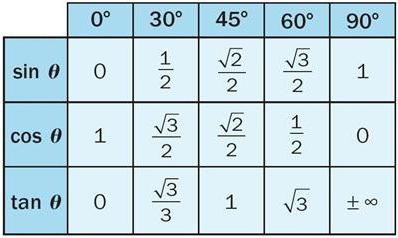
Слово «косинус» появилось намного позже. Этот термин является сокращенным вариантом латинской фразы «дополнительный синус».
Возникновение тангенсов связано с расшифровкой задачи определения длины тени. Термин «тангенс» ввел в X веке арабский математик Абу-ль-Вафа, составивший первые таблицы для определения тангенсов и котангенсов. Но европейские ученые не знали об этих достижениях. Немецкий математик и астроном Регимонтан заново открывает эти понятия в 1467 г. Доказательство теоремы тангенсов – его заслуга. А переводится этот термин как «касающийся».


























