По всей видимости, мало кто сегодня, используя передачу данных по незащищенным каналам связи, представляет себе, что такое алгоритм Диффи-Хеллмана. В принципе, многим это понимание и не нужно. Однако пользователям компьютерных систем, так сказать, более любопытным, разобраться в этом не помешает. В частности, обмен ключами по алгоритму Диффи-Хеллмана может пригодиться юзерам, интересующимся вопросами информационной безопасности и криптографии.
Что такое методика Диффи-Хеллмана?
Если подходить к вопросу о самом алгоритме, пока, не вдаваясь в технические и математические подробности, можно определить его как методику шифрования и дешифровки передаваемой и принимаемой информации между двумя и более пользователями компьютерных или других систем, предполагающих обмен данными с использованием незащищенного канала связи.
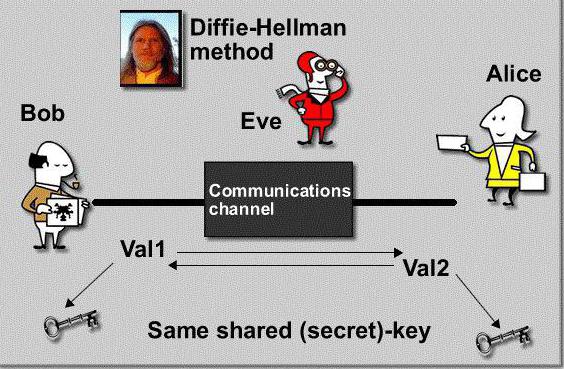
Как уже понятно, при отсутствии защиты самого канала перехватить или модифицировать файлы, находящиеся в процессе передачи-приема, может и злоумышленник. Однако алгоритм распределения ключей Диффи-Хеллмана для доступа к передаваемым и принимаемым данным таков, что постороннее вмешательство практически полностью исключается. При этом общение по используемому каналу связи (без защиты оного) становится безопасным, если обе стороны используют один и тот же ключ.
Предыстория
Сам алгоритм Диффи-Хеллмана был представлен миру еще в далеком 1976 году. Его создателями стали Уитфрид Диффи и Мартин Хеллман, которые в своих изысканиях безопасных и надежных методов шифрования данных опирались на работы Ральфа Меркля, разработавшего так называемую систему распространения публичных ключей.

Но если Меркль разработал исключительно теоретическую базу, Диффи и Хеллман представили публике практическое решение данного вопроса.
Простейшее объяснение
Собственно, сам тест основан на криптографических технологиях шифрования, которые и сейчас удивляют многих специалистов в этой области. Антология шифров включает в себя достаточно большую историю. Суть всего процесса сводится к тому, что имеется два абонента, переписывающихся по электронной почте или обменивающихся некими данными при помощи компьютерных программ. Но защита производится таким образом, что сам алгоритм Диффи-Хеллмана требует, чтобы ключ расшифровки был известен двум сторонам (передающей и принимающей). При этом абсолютно неважно, какая из них сгенерирует начальное случайное число (этот момент поясним при рассмотрении формул вычисления ключей).
Методика шифрования данных ранних периодов
Чтобы было понятнее, заметим, что самым примитивным способом шифрования данных является, например, написание слов не слева направо, как это принято в большинстве письменностей, а справа налево. Точно так же легко можно использовать и замену букв алфавита в сообщении. Скажем, в слове меняется вторая буква на первую, четвертая – на третью и так далее. Сам же документ при взгляде на него может представлять собой полную бессмыслицу. Однако тот, кто написал исходный текст, сообщает тому, кто его должен прочитать, в каком именно порядке следует расположить заданные символы. Это и называется ключом.

Заметьте, большинство до сих пор нерасшифрованных текстов и клинописей древних шумеров и египтян остаются непонятыми крипто-аналитиками всего лишь из-за того, что они не знают, как установить искомую последовательность символов.
Так и в нашем случае - алгоритм Диффи-Хеллмана подразумевает вариант, что ключ расшифровки известен ограниченному количеству пользователей. Правда, и здесь стоит сделать оговорку, поскольку вмешательство в передачу зашифрованных данных такого типа может быть нарушено третьими лицами, если они разгадают систему подстановки или замены символов.
Само собой разумеется, что сегодня существуют достаточно мощные криптосистемы на основе алгоритмов вроде AES, но и они не дают полной гарантии защиты от взлома данных третьей стороной.
Ну а теперь остановимся на самой системе шифрования, ее практическом применении и степени защиты.
Алгоритм Диффи-Хеллмана: назначение
Сам алгоритм создавался таким образом, чтобы обеспечить не только конфиденциальность данных при передаче одной стороной другой, но и для того, чтобы безопасно извлечь их при получении. Грубо говоря, такая система передачи должна обеспечить полноценную защиту по всем возможным каналам общения.

Вспомните хотя бы годы Второй мировой войны, когда разведки всех стран-союзников безуспешно охотились за шифровальной машиной под названием «Энигма», с помощью которой передавались кодированные сообщения на азбуке Морзе. Ведь ее шифр не мог разгадать ни один, даже самый, как мы сейчас говорим, «продвинутый» специалист по криптографии. Только после ее захвата был получен ключ к дешифровке сообщений, передаваемых немецким флотом.
Алгоритм Диффи-Хеллмана: обзор
Итак, сам алгоритм подразумевает использование нескольких базисных понятий. Допустим, у нас имеется простейший случай, когда на связи присутствуют два абонента (пользователя). Обозначим их как A и B.
Они используют два числа X и Y, не являющиеся секретными в данном канале связи, для управления приема-передачи. Вся суть вопроса сводится к тому, чтобы сгенерировать на их основе некое новое значение, которое будет являться ключом. Но! Первый абонент использует большое простое число, а второй – обязательно целое (делящееся без остатка), но меньшее по порядку, чем первое.
Естественно, пользователи договариваются, что эти числа хранятся в тайне. Однако, поскольку канал связи является незащищенным, эти два числа могут стать известными и другим заинтересованным лицам. Именно поэтому пользователи в тех же сообщениях обмениваются секретными ключами для расшифровки сообщений.
Основные формулы вычисления ключа
Принято считать, что алгоритм Диффи-Хеллмана относится к системе так называемого симметричного шифрования, на основе которого появились протоколы асимметричного шифра. Однако, если рассматривать основные аспекты вычисления ключей принимающими сторонами, придется вспомнить хотя бы алгебру.
Итак, допустим, каждый из абонентов генерирует случайные числа a и b. Заранее им известны значения x и y, которые могут быть даже «вшиты» в искомое программное обеспечение.
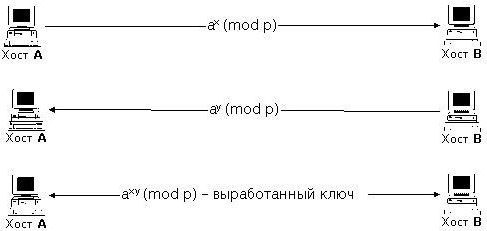
При пересылке или приеме такого сообщения абонент A вычисляет значение ключа, исходя из формулы A =xamod y, а второй использует комбинацию B =xbmod y, после чего следует пересылка расшифрованного ключа первому пользователю. Это первый этап.
Теперь предположим, что третья заинтересованная сторона имеет в своем распоряжении оба вычисленных значения A и B. Все равно она не может вмешаться в процесс передачи данных, поскольку на втором этапе нужно знать, как вычисляется общий ключ.
Исходя из вышеприведенных формул, можно остановиться на вычислении общего ключа. Если посмотреть на алгоритм Диффи-Хеллмана, пример может выглядеть примерно так:
1) первый абонент вычисляет ключ на основе x по формуле Bamod y = xabmod y;
2) второй, исходя из начального числа y и полученного по сетевому протоколу параметра B, определяет ключ на основе имеющегося параметра A: Abmod y =x bamod y.
Как видим, конечные значения даже при перестановке степеней совпадают. Таким образом, расшифровка данных обеими сторонами сводится, как говорится, к единому знаменателю.
Уязвимость при вмешательстве в процесс передачи данных
Как можно было бы предположить, вмешательство третьей стороны не исключается. Однако в данном случае речь идет об изначально задаваемых числах порядка 10100 или даже 10300.
Само собой разумеется, что ни один из сегодня созданных генераторов паролей или кодов доступа определить само число не сможет (разве что начальные и конечные, а не промежуточные параметры для вмешательства в систему передачи). На это потребуется столько времени, что и жизнь на Земле закончится. Тем не менее прорехи в такой системе безопасности все-таки есть.
Чаще всего они связаны со знанием дискретного логарифмирования. Если таковые знания имеются, взломать алгоритм Диффи-Хеллмана можно (но только для начальных и конечных параметров, как уже говорилось выше). Другое дело, что такими знаниями обладают единицы.
Использование алгоритма для платформы Java
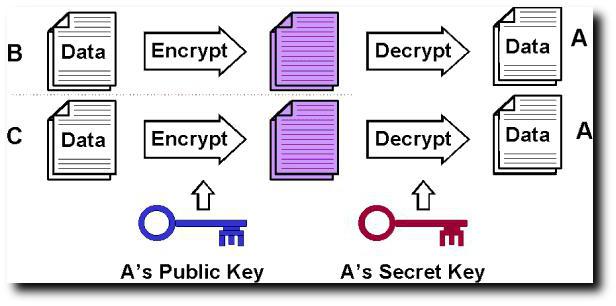
Алгоритм Диффи-Хеллмана на Java используется исключительно при обращениях вроде «клиент-сервер».
Иными словами, сервер находится в стадии ожидания подключения клиентских машин. Когда такое подключение осуществляется, происходит исполнение алгоритма на предмет поиска либо публичного, либо секретного ключа, после чего пользователь может получить беспрепятственный доступ ко всем функциям и данным самого сервера. Иногда это касается даже мобильных систем, правда, об этом мало кто знает, тем более что исполнительная часть работает в невидимом режиме в виде исполняемых скриптов.
Использование алгоритма для платформы C (+/++)
Если посмотреть на алгоритм Диффи-Хеллмана на «C» (+/++), то и здесь не все так гладко. Дело в том, что иногда возникает проблема того, когда сам язык программирования большей частью работает с вычислениями, связанными с плавающей запятой. Именно поэтому при задании целочисленных значений или при попытке округления (даже при возведении в степень) могут наблюдаться неполадки при компиляции. Особенно это касается неправильного использования функции int.
Однако же стоит обратить внимание и на остальные исполняемые компоненты, которые, как правило, представляют собой задание классов, то же возведение в степень или сопутствующие присоединяемые библиотеки GMP.
Современные алгоритмы шифрования
Считается, что алгоритм Диффи-Хеллмана до сих пор превзойти никто не может. Собственно, именно он послужил основой для возникновения таких известных систем защиты в области шифрования данных, как AES128 и AES256.

Однако, как показывает практика, несмотря на доступность чисел, абстрактно не воспринимаемых человеком, большинство систем нынешнего типа используют исключительно значения первого десятка (не более), хотя сам алгоритм подразумевает числа в миллионы раз большие.
Вместо послесловия
В целом, наверное, уже понятно, что собой представляет эта система и каковы её алгоритмические составляющие. Остается только добавить, что она наделена такими огромными возможностями, что ее в полной мере практически никто не использует.
С другой стороны, и уязвимостей в алгоритме явно хватает. Посудите сами: ведь, написав программу для вычисления дискретных логарифмов, практически любой ее создатель может получить доступ не только к начальным параметрам, задаваемым пользователями, но и к общим ключам, которые генерируются в системе шифрования и дешифровки.
В самом простом случае достаточно сделать инсталляцию того же исполняемого Java-апплета, который может быть применен даже в мобильной связи. Естественно, юзер об этом не узнает, но его данные сможет использовать в своих целях любой желающий.





























